Характеристики срабатывания автоматов. Принцип выбора
Автоматические выключатели: характеристики срабатывания и ситуации применения
Автоматический выключатель (автомат) — коммутационное устройство, проводящее ток в нормальном режиме и блокирующее подачу электроэнергии в случаи аварии: перегрузки или короткого замыкания.
Для размыкания электрической цепи автоматические выключатели оборудованы специальными устройствами – расцепителями.
В современных модульных автоматах используется два типа расцепителей:
1) Тепловой – служит для защиты от перегрузкиБиметаллическая пластина, которая изгибается при нагреве, проходящим через нее током, тем самым размыкая контакт. Чем больше перегрузка, тем быстрее нагревается биметаллическая пластинка и быстрее срабатывает расцепитель.
Нормируемые параметры – следующие:
- 1,13 (In) – тепловой расцепитель не срабатывает в течение 1 ч.
- 1,45 (In) – расцепитель срабатывает в течение < 1 ч.
2) Электромагнитный (отсечка) – предназначен для защиты от короткого замыкания
Соленоид с подвижным сердечником, который втягивается при превышении заданного порога тока, мгновенно размыкая электрическую цепь. Отсечка срабатывает при существенном превышении номинального тока (2÷10 In) в зависимости от характеристики срабатывания. Рассмотрим наиболее распространенные автоматы с характеристиками: (B, C, D, K, Z).
1) Характеристика В (3-5 In)
Электромагнитный расцепитель срабатывает при токе, превышающем номинальный в 5 раз. Время отключения <1с. При токе, превышающим номинальный в 3 раза, в течение 4-5 с. сработает тепловой расцепитель. (Обращаем ваше внимание, что для постоянного тока (DC) граница срабатывания будет немного сдвинута (х1,5).
Автоматические выключатели «В» применяются в осветительных сетях с небольшими пусковыми токами (или полным их отсутствием).
2) Характеристика С (5-10 In)
Наиболее распространённые автоматические выключатели. Минимальный ток срабатывания составляет 5 In. При этом значении через 1,5 с сработает тепловой расцепитель, а при 10 кратном превышении номинала, электромагнитный разомкнет цепь меньше, чем за 0,1 с.
Автоматические выключатели «С» подходят для сетей со смешанной нагрузкой (освещение, бытовые электроприборы)
3) Характеристика D (10-20 In)
Характеризуются большой устойчивостью к перегрузке. Тепловой расцепитель разомкнет цепь за 0,4 при превышении порога в 10 In. Срабатывание соленоида произойдет при двадцатикратном превышении номинального тока.
Автоматические выключатели «D» используются для подключения электродвигателей с кратковременными большими токами (пусковые токи)
4) Характеристика K (8-15 In)
Для автоматов этой категории характерна большая разница в показателях для постоянного и переменного токов. Например, электромагнитный расцепитель гарантировано разомкнет цепь за 0,02 с. при достижении значения в 12 In в цепи переменного тока, а для постоянного это значения увеличивается до 18 In. При превышении номинального тока в 1,5 раза в течение 2 мин. сработает тепловой расцепитель.
Автоматы с характеристикой «K» применяются для подключения преимущественно индуктивной нагрузки.
5) Характеристика Z (2-3 In)
Автоматы этой категории также имеют различия в параметрах срабатывания для переменного и постоянного токов.
Электромагнитный расцепитель разомкнет цепь при трёхкратном превышении номинальных параметров в цепи переменного тока и 4,5 In в цепях постоянного тока. Тепловой расцепитель сработает при токе в 1,2 от номинального в течение часа.
Вследствие небольших значений по превышению номинальных параметров, Автоматы «Z» применяются только для защиты высокочувствительной электронной аппаратуры.
Подытоживая вышесказанное отметим, что для бытового использования подходят автоматы с характеристиками: «В» и «С», при возможном подключении электродвигателей с высокими пусковыми токами имеет смысл использовать автоматы категории «Е» (во избежание ложного срабатывания).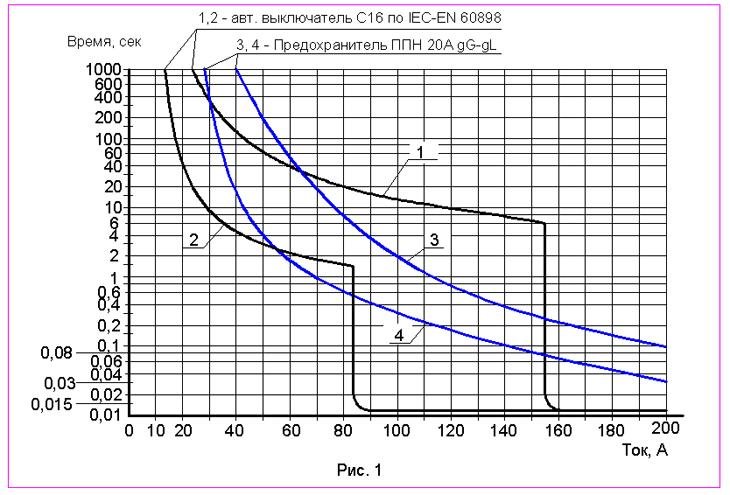
И последнее: если вы сомневаетесь в правильности выбора — обратитесь к профессиональному электрику, не гадайте!
В нашем магазине представлены автоматы всех перечисленных серий, при отсутствии того или иного оборудования его можно легко заказать.
Чтобы узнать подробности и заказать электротехническую продукцию звоните по телефону
(495) 777-05-30Или оставьте сообщение через форму обратной связи в разделе «Контакты».
A, B, C, D, K и Z
На сегодняшний день автоматические выключатели стали незаменимым частью электрической цепи как на производстве, так и в быту. Все автоматические выключатели обладают множеством параметров, один из которых – время токовая характеристика. В данной статьи мы рассмотрим, чем отличаются автоматы с время токовой характеристиками категории A, B, C, D и где данные выключатели применяются.
Работа автоматического выключателя
В сети бывают 2 вида опасных для сети токов:
Сверхтоки вызванный КЗ. Причиной возникновения короткого замыкания является замыкание нейтрального и фазного проводника между собой. В обычном состоянии фазный и нейтральный провод подключены к нагрузке отдельно друг от друга.
Токи перегрузки. Появление таких токов зачастую происходит в том случае, если суммарная мощность подключенных устройств к линии превышает предельно допустимую норму.
Токи перегрузки
Токи перегрузки зачастую бывают немного больше номинального значения тока автомата, поэтому токи перегрузки как правило не вызывают повреждение цепи в случае недолговременной продолжительности действия.
Время срабатывания автоматического выключателя связано с величиной перегрузки. При значительном превышении номинала выключение автомата происходит за считанные секунды, а при небольшом превышении нормы, срабатывание автомата может произойти в течении часа и больше. Данная особенность обусловлена использованием в автомате биметаллической пластины, которая изгибается при нагреве током превышающего норму и тем самым приводит к срабатыванию автомата. Чем большее значение тока, тем быстрее изгибается пластина и тем раньше срабатывает автомат.
Токи КЗ
При правильном выборе автомата, ток КЗ должен приводить к его мгновенному срабатыванию. За обнаружение и немедленную реакцию автомата отвечает электромагнитный расцепитель. Конструктивно расцепитель представляет собой соленоид с сердечником. Под воздействием сверхтока сердечник вызывает мгновенное срабатывание автомата и данное отключение должно происходить в течении доли секунд.
Здесь мы плавно переходим к основному вопросу, которому посвящен наш материал. Существует, как мы уже говорили, несколько классов АВ, различающихся по времятоковой характеристике. Наиболее распространенными из них, которые применяются в бытовых электросетях, являются устройства классов B, C и D. Автоматические выключатели, относящиеся к категории A, встречаются значительно реже. Они наиболее чувствительны и используются для защиты высокоточных аппаратов.
Теперь мы плавно переходим к главному вопросу связанному с срабатыванием автоматических выключателей в зависимости от его времятоковой характеристики. Между собой эти устройства различаются по току мгновенного расцепления. Его величина определяется кратностью тока, проходящего по цепи, к номиналу автомата.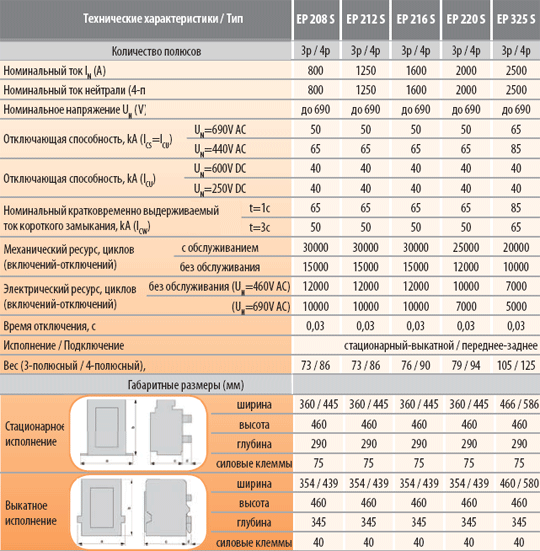
Автоматы типа МА
Главная особенность подобных устройств – отсутствие в них теплового расцепителя. Обычно подобные устройства ставят для защиты электрических моторов и прочих мощных устройств.
Устройства класса А
Автоматы класса А имеют самый высокий порог чувствительности. В устройствах с времятоковой характеристикой А, тепловой расцепитель, как правило срабатывает в случае превышении воздействующей силы тока на 30% больше номинала выключателя.
Стоит учесть, что подобные автоматы устанавливаются в линии, в которой не допустимы даже кратковременные перегрузки. К примеру, это может быть цепь с полупроводниковыми элементами.
Защитные устройства класса B
Устройства категории В используются для установки в линиях, в которые включены приборы освещения, розетки и также в других цепях, в которых отсутствует пусковые токи или они имеют минимальное значение.
Устройства категории С
Устройства типа С весьма распространены в бытовых сетях. Устойчивость к перегрузкам у данных устройств выше, нежели у всех вышеперечисленных. Чтобы произошло срабатывание соленоида электромагнитного расцепителя, требуется превышение проходящего через расцепитель тока в 5 раз выше номинального значения. Тепловой расцепитель срабатывает в случае превышения номинала в 5 раз через 1,5 сек.
Как упоминалось ранее выключатели с времятоковой характеристикой С обычно устанавливаются в бытовых сетях. Данные устройства отлично работают в роли вводных устройств для защиты общей сети.
Вы можете купить автоматические выключатели категории С от лучших производителей:
Автоматы CHINT
Автоматы IEK
Автоматические выключатели категории D
Выключатели категории D имеют наиболее высокую перегрузочную способность. Электромагнитная катушка в устройстве срабатывает при превышении номинала автомата, как минимум в 10 раз.
Электромагнитная катушка в устройстве срабатывает при превышении номинала автомата, как минимум в 10 раз.
Тепловой расцепитель срабатывает через 0,4 сек.
Зачастую устройства категории D применяются в общих сетях зданий и сооружений в роли страховки. Данные устройства срабатывают в том случае, если не произошло своевременное срабатывание автоматов защиты цепи в отдельных помещениях. Также автоматы категории D могут устанавливаться в цепях с большими пусковыми токами.
Вы можете купить автоматические выключатели категории D здесь:
Автоматы CHINT
Автоматы IEK
Защитные устройства категории K и Z
Автоматы категории K и Z встречаются довольно редко. Устройства категории К имеют большой разброс в значениях тока, требуемых для электромагнитного расцепителя. К примеру, для цепи переменного тока данный показатель должен превышать номинал в 12 раз, а в случае применения в цепи постоянного тока, в 18 раз. Электромагнитный соленоид срабатывает через 0,02 сек. Тепловой расцепитель может сработать при превышении номинала всего на 5%.
Из-за своих свойств устройства категории К применяются в цепях с исключительно индуктивной нагрузкой.
Устройства категории Z также имеют различные токи срабатывания соленоида электромагнитного расцепителя, но разброс для данного варианта, не настолько большой, как в выключателях с категорией К. В цепи постоянного тока величина тока должна быть в 4,5 раза выше номинала, а в сетях переменного тока для срабатывания автомата, ток должен превысить автомат в 3 раза. Устройства категории Z обычно используют для защиты электроники.
Что такое время токовые характеристики автоматических выключателей
При нормальной работе электросети и всех приборов через автоматический выключатель протекает электрический ток. Однако если сила тока по каким-либо причинам превысила номинальные значения, происходит размыкание цепи из-за срабатывания расцепителей автоматического выключателя.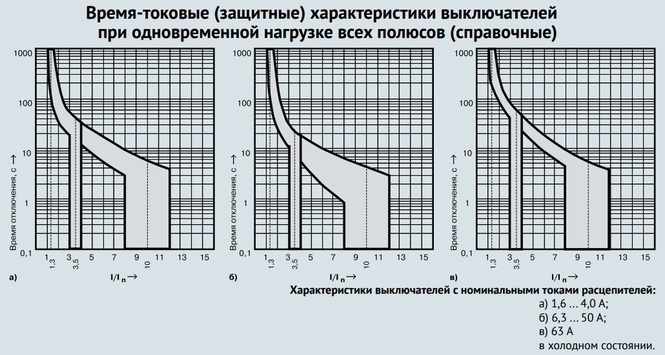
Характеристика срабатывания автоматического выключателя является очень важной характеристикой, которая описывает то, насколько время срабатывания автомата зависит от отношения силы тока, протекающего через автомат, к номинальному току автомата.
Данная характеристика сложна тем, что для ее выражения необходимо использование графиков. Автоматы с одним и тем же номиналом будут при разных превышениях тока по-разному отключаться в зависимости от типа кривой автомата (так иногда называется токовая характеристика), благодаря чему имеется возможность применять автоматы с разной характеристикой для разных типов нагрузки.
Тем самым, с одной стороны, осуществляется защитная токовая функция, а с другой стороны, обеспечивается минимальное количество ложных срабатываний – в этом и заключается важность данной характеристики.
В энергетических отраслях бывают ситуации, когда кратковременное увеличение тока не связано с появлением аварийного режима и защита не должно реагировать на такие изменения. Это же относится и к автоматам.
При включении какого-нибудь мотора, к примеру, дачного насоса или пылесоса, в линии происходит достаточно большой бросок тока, который в несколько раз превышает нормальный.
По логике работы, автомат, конечно же, должен отключиться. К примеру, мотор потребляет в пусковом режиме 12 А, а в рабочем – 5. Автомат стоит на 10 А, и от 12 его вырубит. Что в таком случае делать? Если например поставить на 16 А, тогда непонятно отключится он или нет если заклинит мотор или замкнет кабель.
Можно было бы решить эту проблему, если его поставить на меньший ток, но тогда он будет срабатывать от любого движения. Вот для этого и было придумано такое понятие для автомата, как его «время токовая характеристика».
Какие существуют время токовые характеристики автоматических выключателей и их отличие между собой
Как известно основными органами срабатывания автоматического выключателя являются тепловой и электромагнитный расцепитель.
Тепловой расцепитель представляет собой пластину из биметалла, изгибающуюся при нагреве протекающим током. Тем самым в действие приводится механизм расцепления, при длительной перегрузке срабатывая, с обратнозависимой выдержкой времени. Нагрев биметаллической пластинки и время срабатывание расцепителя напрямую зависят от уровня перегрузки.
Электромагнитный расцепитель является соленоидом с сердечником, магнитное поле соленоида при определенном токе втягивает сердечник, приводящий в действие механизм расцепления – происходит мгновенное срабатывание при КЗ, благодаря чему пострадавший участок сети не будет дожидаться прогревания теплового расцепителя (биметаллической пластины) в автомате.
Зависимость времени срабатывания автомата от силы тока, протекающего через автомат, как раз и определяется время токовой характеристикой автоматического выключателя.
Наверное, каждый замечал изображение латинских букв B, C, D на корпусах модульных автоматов. Так вот они характеризуют кратность уставки электромагнитного расцепителя к номиналу автомата, обозначая его время токовую характеристику.
Эти буквы указывают ток мгновенного срабатывания электромагнитного расцепителя автомата. Проще говоря, характеристика срабатывания автоматического выключателя показывает чувствительность автомата – наименьший ток при котором автомат отключится мгновенно.
Автоматы имеют несколько характеристик, самыми распространенными из которых являются:
- — B — от 3 до 5 ×In;
- — C — от 5 до 10 ×In;
- — D — от 10 до 20 ×In.
Что означают цифры указанные выше?
Приведу небольшой пример. Допустим, есть два автомата одинаковой мощности (равные по номинальному току) но характеристики срабатывания (латинские буквы на автомате) разные: автоматы В16 и С16.
Диапазоны срабатывания электромагнитного расцепителя для В16 составляет 16*(3…5)=48…80А. Для С16 диапазон токов мгновенного срабатывания 16*(5.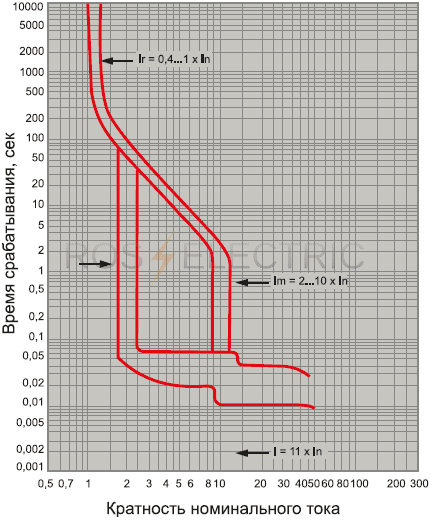 ..10)=80…160А.
..10)=80…160А.
При токе 100 А автомат В16 отключится практически мгновенно, в то время как С16 отключится не сразу а через несколько секунд от тепловой защиты (после того как нагреется его биметаллическая пластина).
В жилых зданиях и квартирах, где нагрузки чисто активные (без больших пусковых токов), а какие-нибудь мощные моторы включаются нечасто, самыми чувствительными и предпочтительными к применению являются автоматы с характеристикой B. На сегодняшний день очень распространена характеристика С, которую также можно использовать для жилых и административных зданий.
Что касается характеристики D, то она как раз годится для питания каких-либо электромоторов, больших двигателей и других устройств, где могут быть при их включении большие пусковые токи. Также через пониженную чувствительность при КЗ автоматы с характеристикой D могут быть рекомендованы для использования как вводные для повышения шансов селективности со стоящими ниже групповыми АВ при КЗ.
Согласитесь логично, что время срабатывания зависит от температуры автомата. Автомат отключится быстрее, если его тепловой орган (биметаллическая пластина) разогретый. И наоборот при первом включении когда биметалл автомата холодный время отключения будет больше.
Поэтому на графике верхняя кривая характеризует холодное состояние автомата, нижняя кривая характеризует горячее состояние автомата.
Пунктирной линией обозначен предельный ток срабатывания для автоматов до 32 А.
Что показано на графике время токовой характеристики
На примере 16-Амперного автомата, имеющего время токовую характеристику C, попробуем рассмотреть характеристики срабатывания автоматических выключателей.
На графике можно увидеть, как протекающий через автоматический выключатель ток влияет на зависимость времени его отключения. Кратность тока протекающего в цепи к номинальному току автомата (I/In) изображает ось Х, а время срабатывания, в секундах – ось У.
Выше говорилось, что в состав автомата входит электромагнитный и тепловой расцепитель. Поэтому график можно разделить на два участка. Крутая часть графика показывает защиту от перегрузки (работа теплового расцепителя), а более пологая часть защиту от КЗ (работа электромагнитного расцепителя).
Как видно на графике если к автомату С16 подключить нагрузку 23 А то он должен отключится за 40 сек. То есть при возникновении перегрузки на 45 % автомат отключится через 40 сек.
На токи большой величины, которые могут привести к повреждению изоляции электропроводки автомат способен реагировать мгновенно благодаря наличию электромагнитного расцепителя.
При прохождении через автомат С16 тока 5×In (80 А) он должен сработать через 0.02 сек (это если автомат горячий). В холодном состоянии, при такой нагрузке, он отключится в пределах 11 сек. и 25 сек. (для автоматов до 32 А и выше 32 А соответственно).
Если через автомат будет протекать ток равный 10×In, то он отключается за 0,03 секунды в холодном состоянии или меньше чем за 0,01 секунду в горячем.
К примеру, при коротком замыкании в цепи, которая защищена автоматом С16, и возникновении тока в 320 Ампер, диапазон времени отключения автомата будет составлять от 0,008 до 0,015 секунды. Это позволит снять питание с аварийной цепи и защитить от возгорания и полного разрушения сам автомат, закоротивший электроприбор и электропроводку.
Автоматы с какими характеристиками предпочтительнее использовать дома
В квартирах по возможности необходимо обязательно применять автоматы категории B, которые являются более чувствительными. Данный автомат отработает от перегрузки так же, как и автомат категории С. А вот о случае короткого замыкания?.
Если дом новый, имеет хорошее состояние электросети, подстанция находится рядом, а все соединения качественные, то ток при коротком замыкании может достигать таких величин, что его должно хватить на срабатывание даже вводного автомата.
Ток может оказаться малым при коротком замыкании, если дом является старым, а к нему идут плохие провода с огромным сопротивлением линии (особенно в сельских сетях, где большое сопротивление петли фаза-нуль) – в таком случае автомат категории C может не сработать вообще. Поэтому единственным выходом из этой ситуации является установка автоматов с характеристикой типа В.
Следовательно, время токовая характеристика типа В является определенно более предпочтительной, в особенности в дачной или сельской местности или в старом фонде.
В быту на вводной автомат вполне целесообразно ставить именно тип С, а на автоматы групповых линий для розеток и освещения – тип В. Таким образом будет соблюдена селективность, и где-нибудь в линии при коротком замыкании вводной автомат не будет отключаться и «гасить» всю квартиру.
Похожие материалы на сайте:
Понравилась статья — поделись с друзьями!
Автоматы категории отключения «B» — Использовать всем! – CS-CS.Net: Лаборатория Электрошамана
Автоматы ABB S200 категории отключения «B»
Совсем мелкая заметка. Я уже затрагивал выбор номинала автомата, и упоминал там автоматы категории B, но не уделил им должного внимания. Исправляю этот косяк.
По возможности СЛЕДУЕТ ОБЯЗАТЕЛЬНО применять в квартирах автоматы категории B! Во-первых, они более чувствительные, а во-вторых кое-как начинает соблюдаться селективность. Мне лень считать, я напишу совсем на пальцах. От перегрузки этот автомат отработает так же, как и автомат категории C. А вот о случае короткого замыкания мы и поговорим.
Написал небольшой пост про селективность автоматов. Почитайте его, там есть ещё несколько интересных моментов!
Вариант первый. Дом новостройка (или старый с электроплитами), и стояк там хороший. Все соединения качественные, подстанция рядом. А значит, обычное омическое сопротивление линии питания довольно низкое. В случае замыкания его ток может достигать таких величин, что его хватит на срабатывание даже вводного автомата. И вы получите то, за что все обижаются: «Что за херня! Мы платили такие огромные деньги, а тут у нас лампочка сгорела, дык вырубило и автомат на свет и ещё и автомат на лестнице!». И действительно, во многих случаях никакой селективности вы не получите, к сожалению. Использование автоматов категории B более-менее (но не во всех случаях) позволяет нормально жить.
В случае замыкания его ток может достигать таких величин, что его хватит на срабатывание даже вводного автомата. И вы получите то, за что все обижаются: «Что за херня! Мы платили такие огромные деньги, а тут у нас лампочка сгорела, дык вырубило и автомат на свет и ещё и автомат на лестнице!». И действительно, во многих случаях никакой селективности вы не получите, к сожалению. Использование автоматов категории B более-менее (но не во всех случаях) позволяет нормально жить.
Вариант второй. Дом старый. С газом. Или дачный, к которому идут хилые провода с большим сопротивлением линии. Тогда может случиться такое западло, что при замыкании его ток будет так мал, что автомат категории C ВООБЩЕ не отработает, а вы потом будете недоумевать, почему это свежий новый щиток — гавно, а дом сгорел. В этом случае, собственно, другого решения, кроме как ставить автоматы B — нет. Ну и ещё по возможности провести ревизию ввода: протянуть все соединения.
Вот такие дела. К сожалению, во многих конторах эти автоматы заказные и идут 2-3 недели с центрального склада ABB. С Электро-мастером у меня есть договорённость о том, что для меня там будут держать эти автоматы по паре коробок всегда, чтобы я мог собрать щиток быстрее. Если народ потянется и на автоматы будет спрос — мы увеличим их оперативный запас.
А вообще, я потихоньку наращиваю объёмы личного склада (тоже типа оперативного запаса). Если раньше там были всякие шинки, наконечники и стяжки — расходники, то теперь есть ещё и пятку автоматов распространённого номинала и некоторые остатки типа «нэ пригодиллосссь», которые используются на следующих заказах.
|
Чувствительность электромагнитных расцепителей регламентируется параметром, называемым характеристикой срабатывания. Это важный параметр, и на нем стоит немного задержаться. Характеристика, иногда ее называют группой, обозначается одной латинской буквой, на корпусе автомата ее пишут прямо перед его номиналом, например надпись C16 означает, что номинальный ток автомата 16А, характеристика С (наиболее, кстати, распространенная). Согласно википедии, автоматические выключатели делятся на следующие типы (классы) по току мгновенного расцепления:
При этом википедия ссылается на ГОСТ Р 50345-2010. Я специально перечитал весь этот стандарт, но ни о каких типах L, Z, K в нем ни разу не упоминается. В другом месте ссылались на уже не действующий ГОСТ Р 50030.2-94 — но я и в нем упоминания о них не нашел. Да и в продаже я что-то не наблюдаю таких автоматов. У европейских производителей классификация может несколько отличаться. В частности, имеется дополнительный тип A (свыше 2·In до 3·In). У отдельных производителей существуют дополнительные кривые отключения. Например, у АВВ имеются автоматические выключатели с кривыми K (8 — 14·In) и Z (2 — 4·In), соответствующие стандарту МЭК 60947-2. В общем, будем иметь в виду, что, кроме B, C и D существуют и иные кривые, но в данной статье будем рассматривать только эти. Сами по себе кривые отключения одинаковы — они вообще показывают зависимость времени срабатывания теплового расцепителя от тока. Разница лишь в том, до какой отметки доходит кривая, после чего она резко обрывается до значения, близкого к нулю. Для характеристик k, l, z кривые несколько другие: кратность гарантированного несрабатывания 1.05, а срабатывания 1.3. Извините, более красивого графика не нашел: Что нам следует иметь в виду, выбирая характеристику отключения? Здесь на первый план выходят пусковые токи того оборудования, которое мы собираемся включать через данный автомат. Нам важно, чтобы пусковой ток в сумме с другими токами в этой цепи не оказался выше тока срабатывания электромагнитного расцепителя (тока отсечки). Проще тогда, когда мы точно знаем, что будет подключаться к нашему автомату, но когда автомат защищает группу розеток, тогда мы только можем предполагать, что и когда туда будет включено. Конечно, мы можем взять с запасом — поставить автоматы группы D. Существует разница в токе срабатывания электромагнитного расцепителя (отсечки) в зависимости от того, переменный или постоянный ток проходит через автомат. Если мы знаем значение переменного тока, при котором срабатывает отсечка, то при постоянном токе срабатывание произойдет при значении, равном амплитудному значению переменного тока. То есть ток нужно умножить примерно на 1.4. Часто приводят вот такие графики (по-моему, не очень верные, но подтверждающие то, что разница между пременным и постоянным током есть): Все написанное выше относится к обычным модульным автоматическим выключателям. У автоматов других типов характеристики несколько другие. Например, кривые срабатывания для автоматов АП-50 — в частности, можно заметить одно существенное отличие: кратности токов гарантийного срабатывания и несрабатывания у них другие. Характеристики срабатывания селективных автоматовДругие кратности и у селективных автоматов (специальные автоматы, применяемые в качестве групповых). Главное отличие селективных автоматов — их срабатывание происходит с небольшой задержкой, для того, чтобы не отключать всю группу, если авария произошла на одной из линий, защищенной нижестоящим автоматом. Усенко К.А., инженер-электрик, |
Технические характеристики автоматических выключателей типа B, C, D, выбор в зависимости от вида нагрузки
Автоматический защитный выключатель (АВ) относится к наиболее часто используемым аппаратам коммутации и защиты в сетях 0,4 кВ. Защитные функции автоматов построены на срабатывании расцепителей двух видов:
- электромагнитного;
- теплового.
Срабатывание электромагнитного расцепителя происходит без выдержки времени и обеспечивает защиту от сверхтоков короткого замыкания.
Тепловой расцепитель имеет интегральную зависимость времени срабатывания от токовой нагрузки. Это обусловлено применением биметаллического элемента, нагреваемого проходящей токовой нагрузкой.
Чем больше значение токовой величины, тем быстрее происходит тепловой изгиб биметалла, освобождение защёлки и, соответственно, отключение автомата. Тепловой расцепитель защищает объект от перегрузки.
Основные принципы автоматической защиты электрических цепей и электрооборудования заключаются в следующем.
Защита коммутационного аппарата должна максимально быстро произвести отключение при возникновении аварийного режима, но при этом не реагировать на кратковременные пусковые токовые всплески электродвигателей и броски намагничивания при включении трансформаторов.
Элементы автоматической защиты АВ не обладают возможностью гибкой настройки параметров срабатывания, как УРЗА. Поэтому для обеспечения защиты нагрузки различного свойства применяют автоматические выключатели, имеющие разную зависимость времени срабатывания от токовой величины. Эта зависимость называется время – токовой характеристикой (ВТХ) автоматического выключателя.
В соответствии с ГОСТ Р 50345 – 2010 время – токовые характеристики автоматов делятся на три типа – B, C, D. Наиболее наглядно сравнительные характеристики автоматов защиты демонстрируют графики ВТХ. По горизонтальной оси графиков отложены значения кратности тока, то есть, отношение фактического тока к номиналу автомата, по вертикальной – время отключения.
Наиболее наглядно сравнительные характеристики автоматов защиты демонстрируют графики ВТХ. По горизонтальной оси графиков отложены значения кратности тока, то есть, отношение фактического тока к номиналу автомата, по вертикальной – время отключения.
ГОСТ регламентирует порядок проведения испытаний по проверке время – токовых характеристик защитного автомата. Проверка отключающей характеристики осуществляется на пяти значениях испытательного тока.
Первые три применяемые в ходе испытаний токовые значения предназначены для проверки срабатывания тепловых расцепителей. Одно из них является величиной нерасцепления, два других – токами расцепления. Два последних испытания проводятся для проверки отключающей способности мгновенного электромагнитного расцепителя.
ИСПЫТАНИЯ ТЕПЛОВЫХ РАСЦЕПИТЕЛЕЙ
Автоматические выключатели с характеристикой типа B, C, D.
I = 1,13*In.
При такой кратности испытываются технические характеристики срабатывания автоматических выключателей всех трёх типов – B, C и D. Токовая нагрузка одновременно пропускается через все полюса выключателя. Критерии отсутствия расцепления одинаковы для всех типов характеристик.
Срабатывание защиты коммутационных аппаратов, имеющих номинальное значение до 63 ампер включительно не должно происходить при проведении технического испытания в течение часа.
Для защитных автоматов номиналом более 63 ампер, срабатывания расцепителя не должно быть в течение двух часов. Начинается испытание при холодном состоянии автомата. Холодным принято считать температуру автомата 30°С.
I = 1,45*In.
В таком режиме также испытываются автоматические выключатели всех трёх видов. К этому испытанию переходят непосредственно после технической проверки током нерасцепления. Ток повышают плавно в течение 5 секунд до величины 1,45*In. Критерии срабатывания расцепителя также одинаковы для защитных коммутационных аппаратов всех технических характеристик.
Автоматические выключатели с номинальными значениями до 63 ампер включительно должны отключиться в течение времени менее одного часа, аппараты номиналом более 63 А – менее чем за 2 часа.
I = 2,55*In.
Данное испытание характеристики расцепителя воздушного выключателя начинают с холодного состояния. Нагрузка должна проходить по всем трём полюсам АВ. Технические критерии расцепления следующие. Отключение защитного коммутационного аппарата с номиналом до 32 ампер включительно происходит более чем за секунду и менее чем за 60 секунд.
Время срабатывания защиты АВ номиналом более 32 ампер лежит в диапазоне от 1 секунды до 120 секунд.
ИСПЫТАНИЯ ЭЛЕКТРОМАГНИТНЫХ РАСЦЕПИТЕЛЕЙ
Автоматические выключатели с технической характеристикой типа B.
I = 3*In.
Целью данной токовой прогрузки является проверка мгновенного электромагнитного расцепителя. Время срабатывания автоматических выключателей любых номиналов, имеющих ВТХ типа B не должно превышать 0,1 секунды.
Токовой нагрузке должны подвергаться все три полюса. Нагрузка расцепления подаётся толчком путём включения вспомогательного выключателя.
I = 5*In.
Токовая проверка пятикратным номиналом также рассчитана на мгновенный расцепитель. Технические условия проведения этого вида испытания такие же, как у предыдущего. АВ холодный, ток подаётся сторонним коммутатором. Автоматическое срабатывание расцепителя должно занимать не более 0,1 секунды.
Автоматические выключатели с технической характеристикой типа C и D.
АВ имеющие ВТХ вида C испытываются 5 – кратным и 10 – кратным током, автоматы с ВТХ D – 10 – кратным и 20 – кратным токами. Время отключения во всех случаях не должно быть более 0,1 секунды. В отдельных случаях АВ типа D могут быть подвергнуты техническим испытаниям 50 – кратным током.
КРИТЕРИИ ВЫБОРА ХАРАКТЕРИСТИКИ
Как видно из описания время – токовых характеристических параметров, к наиболее чувствительным аппаратам относятся АВ, обладающие ВТХ класса B, далее в порядке снижения чувствительности следуют типы C и D.
При выборе автоматических выключателей ВТХ исходят из технического характера защищаемой нагрузки. Процедура выбора выполняется при проектировании электрической части объекта. Выбираемый автомат всегда должен быть чувствительным настолько, насколько это возможно по условиям отстройки от максимальных токовых значений рабочего режима.
Высокочувствительная защита гарантирует быстрое отключение при аварии и обеспечивает пожарную безопасность.
Отключающая техническая характеристика автоматического выключателя типа B больше всего подходит для защиты нагрузки, в составе которой отсутствуют электродвигатели с большими значениями пусковых моментов.
Это:
- осветительная, электронагревательная аппаратура;
- электродвигатели небольшой мощности с лёгким пуском, например воздушные маломощные вентиляторы.
Характеристика C применяется, когда требуется защитить нагрузку с двигателями средней мощности, имеющими заметные пусковые токи.
Характеристика D предназначена для подключения мощных электродвигателей с большими пусковыми моментами.
Часто встречаются технические рекомендации по выбору автоматических коммутационных аппаратов, в которых указывается, что тип B применяется в быту, тип C – в быту и на производстве, тип D – только на производстве. На самом деле защитный коммутационный аппарат выбирается не по назначению нагрузки, а по наличию и величине пусковых токов.
Разумеется, в частном доме вряд ли найдётся много мощных электродвигателей с тяжёлым пуском, требующих защитного коммутационного аппарата класса D, и на производстве существует много участков, где нагрузку составляет только освещение и компьютерная техника.
На таких участках следует применять самые чувствительные автоматы. Вообще, всякое загрубление органов защиты должно быть технически оправданным.
© 2012-2020 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
Какую характеристику автоматического выключателя правильно устанавливать в жилых помещениях
← Новые распределительные щиты New VEGA HAGER — ваш хаб инноваций || Видеообзор шкафы Hager Volta →
Какую характеристику автоматического выключателя правильно устанавливать в жилых помещениях
Для тех, кто не хочет вникать в технические тонкости, какую характеристику автоматического выключателя или дифавтомата (поскольку автоматический выключатель в нем, как часть) применить в защите вашей электросети, предлагаем вниманию рекомендации немецкого производителя HAGER – прочесть и принять:
- Характеристика срабатывания В (3-5 In):
Применяется преимущественно для защиты кабелей и цепей в жилых домах (цепи освещения, розетки)
- Характеристика срабатывания С (5-10 In):
Применяется для защиты кабелей и цепей преимущественно в приборах с повышенным пусковым током (группы ламп, электродвигатели, и т.
 д.)
д.) - Характеристика срабатывания D (10-20 In):
Применяется для защиты кабелей и цепей, особенно в приборах с очень большим пусковым током (сварочные трансформаторы, электродвигатели и т.д.)
Т.е. компания HAGER для жилых помещений рекомендует устанавливать характеристику «В». И ей следуют немецкие электрики. В принципе, подобной рекомендации придерживаются другие европейские производители. Почему же в нашей стране электромонтажники характеристику «В» в жилом фонде не принимают за стандарт, а часто применяют «С» характеристику?
Попробуем разобраться.
Рассмотрим таблицу отключения автоматического выключателя в зависимости от характеристики отключения:
Рис.1 Характеристика «В»
Выпуск автоматических выключателей с разными характеристиками отключения и отсутствие универсальной характеристики обусловлены различными требованиями к защите электрической линии от перегрузок, пусковых токов, короткого замыкания. Из таблицы мы видим, что самый быстрый и чувствительный автомат с «В» характеристикой, самый медленный и не чувствительный к пиковым нагрузкам – автомат с характеристикой «D».
Рис.2 характеристика «C»
Характеристика «С» кажется оптимальной, поскольку находится посередине графика (см. выше). Так ли это? Тот факт, что автоматы типа C сейчас активно применяются, не означает, что тип C «лучше» или «более продвинутый». Это просто два разных типа для разных условий, но технологический уровень их исполнения одинаков. И цена, практически, тоже одинакова.
Рис.3 характеристика «D»
Следует отметить, что в современной высококачественной бытовой технике, благодаря применению специальных технологий, пусковые токи значительно меньше, чем были раньше, даже если используется импульсный блок питания. Поэтому, если вы оснастили квартиру или коттедж современной техникой, можно сделать выбор в пользу защитных автоматов типа «B». При этом можно повысить надежность энергоснабжения, реализовав принцип селективного отключения. Он заключается в том, что из-за задержки по времени в срабатывании вышестоящего защитного автомата относительно нижестоящего предотвращается отключение питания по всему коттеджу или по всей квартире. Самый экономичный способ реализации селективной защиты — поставить вводной автомат типа С, а в качестве нижестоящих использовать автоматы типа B.
Он заключается в том, что из-за задержки по времени в срабатывании вышестоящего защитного автомата относительно нижестоящего предотвращается отключение питания по всему коттеджу или по всей квартире. Самый экономичный способ реализации селективной защиты — поставить вводной автомат типа С, а в качестве нижестоящих использовать автоматы типа B.
Еще одно хорошее преимущество характеристики «В» в квартире. Автоматы с такой характеристикой лучше щадят вашу сеть при коротком замыкании, т.к. раньше отключаются и не настолько требовательны к сечению проводников, как характеристика «С».
Выбор характеристики автоматических выключателей остается за вами. Можно полностью установить с характеристикой «С».
Основы теории автоматов
Введение
Теория автоматов — увлекательная теоретическая область информатики. Он заложил свои корни в 20 веке, когда математики начали разрабатывать — как теоретически, так и буквально — машины, которые имитировали определенные черты человека, выполняя вычисления более быстро и надежно. Само слово automaton , тесно связанное со словом «автоматизация», обозначает автоматические процессы, осуществляющие производство определенных процессов.Проще говоря, теория автоматов имеет дело с логикой вычислений относительно простых машин, называемых автоматами . С помощью автоматов компьютерные ученые могут понять, как машины вычисляют функции и решают проблемы, и, что более важно, что означает определение функции как вычислимой или описание вопроса как разрешимой .
Автоматы — это абстрактные модели машин, которые выполняют вычисления на входе, проходя через серию состояний или конфигураций.В каждом состоянии вычислений функция перехода определяет следующую конфигурацию на основе конечной части текущей конфигурации. В результате, как только вычисление достигает принимающей конфигурации, оно принимает этот ввод. Самый общий и мощный автомат — это машина Тьюринга .
Самый общий и мощный автомат — это машина Тьюринга .
Основная цель теории автоматов — разработать методы, с помощью которых компьютерные специалисты могут описывать и анализировать динамическое поведение дискретных систем, в которых периодически производится выборка сигналов.Поведение этих дискретных систем определяется тем, как система построена из запоминающих и комбинационных элементов. Характеристики таких машин включают:
- Входы: предполагается, что представляют собой последовательности символов, выбранных из конечного набора I входных сигналов. А именно, набор I — это набор {x 1 , x, 2 , x 3 … x k }, где k — количество входов.
- Выходы: последовательностей символов, выбранных из конечного набора Z.А именно, набор Z — это набор {y 1 , y 2 , y 3 … y m }, где m — количество выходов.
- Состояния: конечное множество Q , определение которого зависит от типа автомата.
Существует четырех основных семейств автоматов :
- Конечный автомат
- Выталкивающие автоматы
- Линейно-ограниченные автоматы
- Машина Тьюринга
Вышеупомянутые семейства автоматов можно интерпретировать в иерархической форме, где конечный автомат является простейшим автоматом, а машина Тьюринга — наиболее сложным.Основное внимание в этом проекте уделяется конечному автомату и машине Тьюринга. Машина Тьюринга — это машина с конечным числом состояний, но обратное неверно.
[вверху]
Конечные автоматы
Увлекательная история того, как конечные автоматы стали отраслью информатики, иллюстрирует широкий спектр их приложений. Первыми, кто рассмотрел концепцию конечного автомата, была группа биологов, психологов, математиков, инженеров и некоторых из первых ученых-информатиков.Все они были объединены общим интересом: моделировать мыслительный процесс человека, будь то мозг или компьютер. Уоррен МакКаллох и Уолтер Питтс, два нейрофизиолога, были первыми, кто представил описание конечных автоматов в 1943 году. Их статья, озаглавленная «Логическое исчисление, имманентное нервной деятельности», внесла значительный вклад в изучение теории нейронных сетей, теории автоматы, теория вычислений и кибернетика. Позже двое компьютерных ученых Г. Мили и Э.Ф. Мур обобщили теорию на гораздо более мощные машины в отдельных статьях, опубликованных в 1955-56 гг.Конечные автоматы, машина Мили и машина Мура, названы в честь их работы. В то время как машина Мили определяет свои выходные данные через текущее состояние и входные данные, выходные данные машины Мура основываются только на текущем состоянии.
Первыми, кто рассмотрел концепцию конечного автомата, была группа биологов, психологов, математиков, инженеров и некоторых из первых ученых-информатиков.Все они были объединены общим интересом: моделировать мыслительный процесс человека, будь то мозг или компьютер. Уоррен МакКаллох и Уолтер Питтс, два нейрофизиолога, были первыми, кто представил описание конечных автоматов в 1943 году. Их статья, озаглавленная «Логическое исчисление, имманентное нервной деятельности», внесла значительный вклад в изучение теории нейронных сетей, теории автоматы, теория вычислений и кибернетика. Позже двое компьютерных ученых Г. Мили и Э.Ф. Мур обобщили теорию на гораздо более мощные машины в отдельных статьях, опубликованных в 1955-56 гг.Конечные автоматы, машина Мили и машина Мура, названы в честь их работы. В то время как машина Мили определяет свои выходные данные через текущее состояние и входные данные, выходные данные машины Мура основываются только на текущем состоянии.
| Уоррен МакКаллох и Уолтер Питтс (источник) | |
Автомат, в котором множество состояний Q содержит только конечных элементов, называется конечным автоматом (FSM).Конечные автоматы — это абстрактные машины, состоящие из набора состояний (набор Q), набора входных событий (набор I), набора выходных событий (набор Z) и функции перехода между состояниями. Функция перехода между состояниями принимает текущее состояние и входное событие и возвращает новый набор выходных событий и следующее состояние. Следовательно, его можно рассматривать как функцию, которая отображает упорядоченную последовательность входных событий в соответствующую последовательность или набор выходных событий.
Функция перехода между состояниями: I → Z
Конечные автоматы — идеальные модели вычислений для небольшого объема памяти и не поддерживают память.Эта математическая модель машины может достигать только конечного числа состояний и переходов между этими состояниями. Его основное применение — математический анализ проблем. Конечные машины также используются для других целей, помимо общих вычислений, например, для распознавания обычных языков.
Чтобы полностью понять концептуально конечный автомат, рассмотрим аналогию с лифтом:Лифт — это механизм, который не запоминает все предыдущие запросы на обслуживание, кроме текущего этажа, направления движения (вверх или вниз) и сбора еще неудовлетворенных запросов на обслуживание.Следовательно, в любой момент времени работающий лифт будет определяться следующими математическими терминами:
- Состояния: конечный набор состояний для отражения прошлой истории запросов клиентов.
- Входы: конечный набор входов, в зависимости от количества этажей, на которые может подняться лифт. Мы можем использовать набор I, размер которого равен количеству этажей в здании.
- Выходы: конечных наборов выходных данных, в зависимости от необходимости подъема или опускания лифта в соответствии с потребностями клиентов.
Конечный автомат формально определяется как кортеж из 5 (Q, I, Z, ∂, W), такой что:
- Q = конечный набор состояний
- I = конечный набор входных символов
- Z = конечный набор выходных символов
- ∂ = отображение I x Q в Q, называемое функцией перехода состояний, то есть I x Q → Q
- W = отображение W I x Q на Z, называемое функцией вывода
- A = набор состояний принятия, где F — подмножество Q
Исходя из математической интерпретации выше, можно сказать, что конечный автомат содержит конечное число состояний.Каждое состояние принимает конечное количество входов, и каждое состояние имеет правила, которые описывают действие машины для любого входа, представленного в функции отображения перехода состояний. В то же время ввод может вызвать изменение состояния машины. Для каждого входного символа есть ровно один переход из каждого состояния. Кроме того, любой 5-кортежный набор, который принимается недетерминированными конечными автоматами, также принимается детерминированными конечными автоматами.
При рассмотрении конечных автоматов важно иметь в виду, что механический процесс внутри автоматов, который приводит к вычислению выходных данных и изменению состояний, не акцентируется и не углубляется в детали; вместо этого он считается «черным ящиком», как показано ниже:Имея конечный постоянный объем памяти, внутренние состояния конечного автомата не несут никакой дополнительной структуры.Их легко представить с помощью диаграмм состояний, как показано ниже:
Диаграмма состояний иллюстрирует работу автомата. Состояния представлены узлами графов, переходами стрелками или ветвями , а соответствующие входы и выходы обозначены символами. Стрелка, входящая слева в q 0 , показывает, что q 0 является начальным состоянием станка. Движения, не связанные с изменением состояний, обозначены стрелками по сторонам отдельных узлов.Эти стрелки известны как петли .
Существует нескольких типов конечных автоматов , которые можно разделить на три основные категории:
- акцепторы : либо принимать, либо не принимать
- распознаватели : либо распознают ввод, либо нет
- преобразователи : генерировать выходной сигнал по заданному входу
Применения конечных автоматов можно найти в самых разных областях.Они могут работать с языками с конечным числом слов (стандартный случай), бесконечным числом слов (автоматами Рабина, автоматами Бирша), различными типами деревьев и в аппаратных схемах, где вход, состояние и выход являются битовыми. векторы фиксированного размера.
[вверху]
Конечное состояние против машин Тьюринга
Простейший автомат, используемый для вычислений, — это конечный автомат. Он может вычислять только очень примитивные функции; следовательно, это не адекватная модель вычислений.Кроме того, неспособность конечного автомата обобщать вычисления снижает его мощность.
Ниже приведен пример, иллюстрирующий разницу между конечным автоматом и машиной Тьюринга:
Представьте себе современный процессор. Каждый бит в машине может находиться только в двух состояниях (0 или 1). Следовательно, существует конечное число возможных состояний. Кроме того, при рассмотрении частей компьютера, с которыми взаимодействует ЦП, существует ограниченное количество возможных входов от компьютерной мыши, клавиатуры, жесткого диска, различных слотовых карт и т. Д.В результате можно сделать вывод, что ЦП можно смоделировать как конечный автомат.
Теперь рассмотрим компьютер. Хотя каждый бит в машине может находиться только в двух разных состояниях (0 или 1), внутри компьютера в целом существует бесконечное количество взаимодействий. Становится чрезвычайно трудно моделировать работу компьютера в рамках ограничений конечного автомата. Однако более высокоуровневые, бесконечные и более мощные автоматы были бы способны выполнить эту задачу.
Всемирно известный ученый-компьютерщик Алан Тьюринг разработал первую «бесконечную» (или неограниченную) модель вычислений: машину Тьюринга в 1936 году для решения задачи Entscheindungs . Машину Тьюринга можно рассматривать как конечный автомат или блок управления, снабженный бесконечным хранилищем (памятью). Его «память» состоит из бесконечного числа одномерных массивов ячеек. Машина Тьюринга — это, по сути, абстрактная модель современного компьютерного исполнения и хранения, разработанная для того, чтобы дать точное математическое определение алгоритма или механической процедуры.
В то время как автомат называется конечным , если его модель состоит из конечного числа состояний и функций с конечными строками ввода и вывода, бесконечные автоматы имеют «аксессуар» — либо стек, либо ленту, которую можно перемещать вправо. или уехал, и может соответствовать тем же требованиям, что и машина.
Машина Тьюринга формально определяется набором [Q, Σ, Γ, δ, q 0 , B, F], где
- Q = конечный набор состояний, из которых одно состояние q 0 является начальным состоянием
- Σ = подмножество Γ, не включая B, это набор входных символов
- Γ = конечный набор допустимых обозначений ленты
- δ = функция следующего перемещения , функция отображения из Q x Γ в Q x Γ x {L, R}, где L и R обозначают направления влево и вправо соответственно
- q 0 = в наборе Q в качестве начала состояние
- B = символ Γ, как пробел
- F ⊆ Q набор из конечных состояний
Следовательно, основное различие между машиной Тьюринга и двусторонними конечными автоматами (FSM) заключается в том, что машина Тьюринга способна изменять символы на своей ленте и моделировать выполнение и хранение на компьютере.По этой причине можно сказать, что машина Тьюринга способна моделировать все вычисления, которые сегодня можно вычислить с помощью современных компьютеров.
[вверху]
Введение в конечные автоматы — GeeksforGeeks
Конечные автоматы (FA) — это простейшая машина для распознавания шаблонов. Конечный автомат или конечный автомат — это абстрактная машина, состоящая из пяти элементов или кортежей. У него есть набор состояний и правил для перехода из одного состояния в другое, но это зависит от применяемого входного символа.По сути, это абстрактная модель цифрового компьютера. На следующем рисунке показаны некоторые важные особенности общей автоматизации.
Рисунок: Характеристики конечных автоматов
На приведенном выше рисунке показаны следующие особенности автоматов:
- Вход
- Выход
- Состояния автоматов
- Отношение состояний
- Выходное отношение
Конечный автомат состоит из следующего:
Q: Конечный набор состояний.Σ: набор входных символов. q: Исходное состояние. F: набор конечных состояний. δ: функция перехода.
Формальная спецификация машины:
{Q, Σ, q, F, δ}.
FA характеризуется двумя типами:
1) Детерминированные конечные автоматы (DFA)
DFA состоит из 5 кортежей {Q, Σ, q, F, δ}.
Q: набор всех состояний.
Σ: набор входных символов. (Символы, которые машина принимает в качестве входных данных)
q: Исходное состояние. (Стартовое состояние машины)
F: набор конечного состояния.δ: функция перехода, определяемая как δ: Q X Σ -> Q.
В DFA для определенного входного символа машина переходит только в одно состояние. Функция перехода определяется в каждом состоянии для каждого входного символа. Также в DFA нулевое (или ε) перемещение не разрешено, то есть DFA не может изменить состояние без какого-либо входного символа.
Например, нижеприведенный DFA с Σ = {0, 1} принимает все строки, заканчивающиеся на 0.
Рисунок: DFA с Σ = {0, 1}
Важно отметить, что там может быть много возможных DFA для шаблона .Обычно предпочтительнее DFA с минимальным количеством состояний.
2) Недетерминированные конечные автоматы (NFA)
NFA похожи на DFA, за исключением следующих дополнительных функций:
1. Разрешено нулевое (или ε) перемещение, т.е. он может двигаться вперед без чтения символов.
2. Возможность передачи в любое количество состояний для конкретного входа.
Однако эти вышеупомянутые функции не добавляют мощности NFA. Если мы сравним оба с точки зрения мощности, оба эквивалентны.
Из-за вышеупомянутых дополнительных функций NFA имеет другую функцию перехода, остальные такие же, как DFA.В.
Как вы можете видеть, функция перехода предназначена для любого входа, включая ноль (или ε), NFA может перейти в любое количество состояний.
Например, ниже представлен NFA для указанной выше проблемы
NFA
Следует отметить одну важную вещь: в NFA, если какой-либо путь для входной строки приводит к конечному состоянию, то входная строка принимается . Например, в приведенной выше NFA есть несколько путей для входной строки «00». Поскольку один из путей ведет к конечному состоянию, «00» принимается вышеуказанным NFA.
Некоторые важные моменты:
В случае DFA δ: Q X Σ -> Q В случае NFA δ: Q X Σ -> 2 Q
Теперь, если вы понаблюдаете, вы обнаружите, что Q X Σ -> Q является частью Q X Σ -> 2 Q .
На правой стороне Q является подмножеством 2 Q , что указывает на то, что Q содержится в 2 Q или Q является частью 2 Q , однако обратное неверно.Таким образом, математически мы можем заключить, что каждый DFA является NFA, но не наоборот . Тем не менее, есть способ преобразовать NFA в DFA, поэтому существует эквивалентный DFA для каждого NFA .
1. И NFA, и DFA имеют одинаковую мощность, и каждый NFA может быть преобразован в DFA.
2. Как в DFA, так и в NFA может быть несколько конечных состояний.
3. NFA — это скорее теоретическая концепция.
4. DFA используется в лексическом анализе в компиляторе.
См. Тест по регулярным выражениям и конечным автоматам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсужденной выше
12. Автоматические раскрытия: PDA-DPDA
Описание
Автомат выталкивания (КПК) — это конечный автомат, который имеет дополнительное хранилище стека. Переходы, совершаемые машиной, основаны не на только на входе и в текущем состоянии, но и в стеке. Формальное определение (в нашем учебнике) таково, что КПК это:M = (K, Σ, Γ, Δ, s, F)куда
- K = набор конечных состояний
- Σ = конечный входной алфавит
- Γ = алфавит с конечным стеком
- s ∈ K: начальное состояние
- F ⊆ K: конечные состояния
- Отношение перехода, Δ — это конечных подмножеств (K × (Σ∪ {ε}) × Γ * ) × (K × Γ * )
- текущее состояние — p
- текущий входной символ — σ
- строка наверху стопки — это α
- новое состояние
- заменить α в верхней части стека на β (нажмите α и нажмите β)
- текущее состояние — p
- строка наверху стопки — это α
- изменение состояния — q
- заменить α в верхней части стека на β
Конфигурация машины, выработка, приемка
Конфигурация машины — это элемент K × Σ * × Γ * .(p, w, z) = (текущее состояние, необработанный ввод, содержимое стека)Мы определяем обычную урожайность за один шаг соотношением :
(p, σw, αz) & vdash; (q, w, βz), если ((p, σ, α), (q, β)) ∈ ∆ или же (p, w, αz) & vdash; (q, w, βz), если ((p, ε, α), (q, β)) ∈ ∆Как и ожидалось, дает отношение , & vdash; *, является рефлексивным, транзитивным замыканием & vdash ;. Строка w принимается КПК , если
(s, w, ε) & vdash; * (f, ε, ε)А именно, из начального состояния с пустым стеком мы
- обработать всю строку,
- закончить в конечном состоянии
- заканчиваются пустой стопкой.
Графическое представление и ε-переход
В книге об этом не говорится, но есть графическое изображение КПК.Переход((p, x, α), (q, β)), где x = ε или x ∈ Σбудет изображаться так (соответственно):
| или |
α / βпредставляет эти действия:
- верх стека должен соответствовать α
- , если мы сделаем переход, pop α и push β
- Δ это отношение
- есть ε-переходы по входу
- есть ε-переходы по содержимому стека
Примеры палиндрома
Это примеры 3.3.1 и 3.3.2 в учебнике. Первый из них:| {x ∈ {a, b, c} *: x = wcw R для w ∈ {a, b} *} |
ε в состоянии s ab в состоянии s с непустым стеком abcab в состоянии f с неиспользованным вводом и непустым стеком abcb в состоянии f с непустым стеком abcbab в состоянии f с неиспользованным вводом и пустым стекомОбратите внимание, что этот КПК детерминирован в том смысле, что в переходах нет выбора.Второй пример:
| {x ∈ {a, b} *: x = ww R для w ∈ {a, b} *} |
| Этот КПК идентичен предыдущему , за исключением ε-перехода |
A
n b n язык Язык L = {w ∈ {a, b} *: w = a n b n , n ≥ 0}. Вот два КПК для L:| и |
Язык, равный a и b
Это пример 3.3.3 из учебника. Воспользуемся удобными обозначениями:# σ (w) = количество вхождений σ в wЯзык L = {w ∈ {a, b} *: #a (w) = #b (w)}. Вот КПК: Как видите, большая часть активности связана с поведением в состоянии q.Идея состоит в том, чтобы стек поддерживал превышение одного символа над другим. Чтобы достичь нашей цели, мы должны знать, когда стек пуст.
Знания о пустом стеке
В КПК нет встроенного механизма, позволяющего определить, пусто или нет. Важно понимать, что переход:| x = σ ∈ Σ или ε |
Поведение КПК
Эти три группы циклических переходов в состоянии q представляют собой соответствующие функции:- введите a без b в стеке: нажмите
- вход b без значков a в стеке: нажмите b
- введите a с буквами b в стеке: pop b; или же, введите b с символом a в стеке: pop a
DPDA / DCFL
Учебник определяет DPDA (детерминированные КПК) и DCFL (детерминированные CFL). во вводной части раздела 3.7. Согласно определению из учебника, DPDA — это КПК, в котором ни одно состояние p не имеет двух разных исходящих переходов((p, x, α), (q, β)) и ((p, x ′, α ′), (q ′, β ′))которые совместимы с в том смысле, что оба могут быть применены.DCFL — это, по сути, язык, принятый DPDA, но нам нужно уточнить это дальше. Мы хотим утверждать, что язык L = {w ∈ {a, b} *: #a (w) = #b (w)} является детерминированным контекстно-свободным в том смысле, что его принимает DPDA. В указанном выше КПК единственной недетерминированной проблемой является угадывание конец ввода; однако эта форма недетерминизма считается искусственной. Когда мы рассматриваем, поддерживает ли язык L DPDA или нет, выделенный символ конца ввода всегда добавляется к строкам на языке.Формально язык L над Σ является детерминированный контекст без , или L — DCFL, если
L $ принимается DPDA Mгде $ — выделенный символ, не принадлежащий Σ. Значение состоит в том, что мы можем разумно использовать знания. конца ввода, чтобы решить, что делать со стеком. В нашем случае мы бы просто заменили переход на финальный заявить: С этим изменением наш КПК теперь DPDA:
a * b * примеры
Две распространенные вариации на буквы а, за которыми следует б.Когда они равны, дно стека не требуется. Когда они неравны, нужно быть готовым чтобы распознать, совпадают ли сложенные a полностью или нет. а. {a n b n : n ≥ 0} б. {a m b n : 0 ≤ m| состояние | вход | стек |
| 1 | abb $ | с |
| 1 | bb $ | ac |
| 2 | млрд $ | ac |
| 2 | $ | с |
| 3 | ε | ε |
| состояние | вход | стек |
| 1 | abbbb $ | с |
| 1 | BBBB $ | ac |
| 2 | баррелей $ | ac |
| 2 | bb $ | с |
| 3 | млрд $ | ε |
| 3 | $ | ε |
| 3 | ε | ε |
| состояние | вход | стек |
| 1 | ab $ | с |
| 1 | млрд $ | ac |
| 2 | $ | ac |
| состояние | вход | стек |
| 1 | ba $ | с |
| 2 | a | долл. СШАс |
Обратите внимание, что строка типа abbba также не работает из-за невозможность потреблять самую последнюю а.
CFL / PDA эквивалент
Цель раздела 3.4 учебника — доказать, что КЛЛ и КПК эквивалентны, а именно, для каждого КЛЛ, G существует КПК M такое, что L (G) = L (M), и наоборот. Автор разбивает это на две леммы:- Лемма 3.4.1: с учетом грамматики построить КПК и показать эквивалентность
- Лемма 3.4.2: для КПК постройте грамматику и покажите эквивалентность
Грамматика конструкции КПК
Эта конструкция довольно проста. Для G = (V, Σ, R, S), КПК будет производить крайний левый вывод строки w ∈ L (G). КПК есть
M = ({0,1}, Σ, V, Δ, 0, {1})
А именно есть всего два состояния
КПК сразу переходит в конечное состояние — 1 с начала
символ в стеке, а затем остается в этом состоянии.Это переходы в Δ:1: ((0, ε, ε), (1, S)) 2: ((1, ε, A), (1, α)) при A → α 3: ((1, σ, σ), (1, ε)) для σ ∈ ΣЭтот сконструированный КПК по своей сути недетерминирован; если есть выбор правил для применения к нетерминалу, то существует недетерминированный выбор этапов обработки. Графически представление таково: Сказать, что G и M эквивалентны, означает что L (M) = L (G), или, рассматривая произвольную строку w ∈ Σ * :
S ⇒ * w ⇔ (0, w, ε) & vdash; * (1, ε, ε)
Грамматика для
n b n Используйте грамматику: S & xrarr; ε | aSb Вот КПК: Простой запуск:& vdash; (0, aabb, ε) & vdash; (1, аабб, S) & vdash; (1, аабб, аСб) & vdash; (1, абб, сб) & vdash; (1, abb, aSbb) & vdash; (1, bb, Sbb) & vdash; (1, бб, бб) & vdash; (1, б, б) & vdash; (1, ε, ε)
Грамматика выражений
Наиболее информативными являются примеры, в которых существует возможность не используя крайний левый вывод, такой как наша грамматика выражений:E → E + T | Т Т → Т * F | F F → (E) | аМы легко можем сопоставить крайний левый вывод a + a * a с соответствующим обработка конфигурации машины следующим образом:
& vdash; (0, а + а * а, ε) & vdash; (1, а + а * а, Е) & vdash; (1, a + a * a, E + T) E ⇒ E + T & vdash; (1, а + а * а, Т + Т) ⇒ Т + Т & vdash; (1, а + а * а, F + T) ⇒ F + T & vdash; (1, а + а * а, а + Т) ⇒ а + Т & vdash; (1, + a * a, + T) & vdash; (1, а * а, Т) & vdash; (1, а * а, Т * F) ⇒ а + Т * F & vdash; (1, a * a, F * F) ⇒ a + F * F & vdash; (1, а * а, а * F) ⇒ а + а * F & vdash; (1, * а, * F) & vdash; (1, а, F) & vdash; (1, а, а) ⇒ а + а * а & vdash; (1, ε, ε)
Грамматика для КПК
Для простоты или простоты предположим, что ⇒ означает крайний левый шаг вывода.Утверждение: для w ∈ Σ * α ∈ (V-Σ) V * ∪ {ε}:S ⇒ * wα ⇔ (1, w, S) | - * (1, ε, α)
(Доказательство ⇒):
Индукция по длине самого левого вывода.S ⇒ n α ′ ⇒ wαЗатем, поскольку последний шаг был крайним левым, мы можем написать:
α ′ = xAβ для x ∈ Σ *а потом
xzβ = wα для A → z (A)По индукции, поскольку S ⇒ n xAβ:
(1, x, S) | - * (1, ε, Aβ)Кроме того, применив переход типа 2, мы имеем:
(1, ε, Aβ) | - (1, ε, zβ)Собираем эти два вместе:
(1, x, S) | - * (1, ε, zβ) (B)Глядя на (A) , мы видим, что строка x должна быть префиксом w, поскольку α начинается с нетерминала или пусто.Написать
w = xy и, следовательно, zβ = yα (C)Как следствие (В) получаем:
(1, ху, S) | - * (1, у, zβ) (D)Объедините (C) и (D) , чтобы получить:
(1, w, S) | - * (1, y, yα) (E)Применить | y | переходы типа 3, чтобы получить
(1, y, yα) | - * (1, ε, α) (F)Объедините (E) и (F) , чтобы получить желаемый результат:
(1, w, S) | - * (1, ε, α)
(Проба ⇐):
Доказательство в этом направлении проводится индукцией по количество тип-2 шагов в деривации.Это ограничение делает все доказательство проще, чем обратное. что мы только что доказали. Перейдем к шагу индукции. Предположим, что верно до n шагов, и докажем, что верно для n + 1 шагов типа 2. Написать:(1, w, S) | - * (1, y, Aβ) | - (1, y, zβ) | - * (1, ε, α)где использование правила
A ⇒ zпредставляет собой последний шаг типа 2, а последняя часть цепочки состоит только из ступеней типа 3. Строка y должна быть суффиксом w, и так что записав
w = xy, мы имеем:
(1, xy, S) | - * (1, y, Aβ)и поэтому,
(1, x, S) | - * (1, ε, Aβ)Поэтому по индукции:
S ⇒ * xAβи следовательно,
S ⇒ * xzβ (А)Теперь, если мы посмотрим на последнюю часть:
(1, y, zβ) | - * (1, ε, α)Заметим, что, поскольку он состоит из , только тип-3 переходы, должно быть, что
yα = zβ (B)и так, сложив вместе (A) и (B) , получим:
S ⇒ * xyαЗная, что w = xy, мы получаем желаемый результат:
S ⇒ * wα
(PDF) Характеристические формулы для временных автоматов
[4] Дж.Baeten and J. Klop, ред., Proceedings CONCUR 90, Amsterdam,
vol. 458 конспектов лекций по информатике, Springer-Verlag, 1990.
[5] Б. Блум, С. Истрайл, А. Р. Мейер, Бисимуляция не может быть отслежена
, J. Assoc. Comput. Mach., 42 (1995), стр. 232–268.
[6] М. Браун, Э. Кларк и О. Грю
Умберг, Характеризация конечных
структур Крипке в временной логике высказываний, Теоретические вычисления.
Sci., 59 (1988), стр. 115–131.
[7] Э. Кларк и Э. Эмерсон, Разработка и синтез скелетов синхронизации
с использованием временной логики времени ветвления, в Proceedings of the
Workshop on Logic of Program, Yorktown Heights, D. Kozen, ed.,
об. 131 конспектов лекций по информатике, Springer-Verlag, 1981,
, стр. 52–71.
[8] Э. Кларк, О. Грю
Умберг и Д. Пелед, Проверка моделей, MIT
Press, 2000.
[9] Р. Кливленд и Б. Стеффен, Вычисление поведенческих отношений,
, по логике ICALP ’91: Автоматы, языки и программирование, J.L.
Альберт, Б. Моньен и М. Р. Арталехо, ред., Т. 510 конспектов лекций
по информатике, Мадрид, июль 1991 г., Springer-Verlag, стр. 127–138.
[10], Алгоритм проверки модели в линейном времени для свободного модального µ-исчисления
, Формальные методы в проектировании систем, 2 (1993),
pp. 121–147.
[11] Дж. Энгельфриет, Детерминированность → (эквивалентность наблюдения = эквивалентность трассы
), Теоретические вычисления. Sci., 36 (1985), стр. 21–25.
[12] Р. Дж. Ван Глаббек, Линейный временной спектр с ветвлением времени, в
Баетен и Клоп [4], стр. 278–297.
[13] С. Граф и Дж. Сифакис, Модальная характеристика наблюдаемой конгруэнтности
на конечных условиях CCS, Информация и управление, 68 (1986),
pp. 125–145.
[14] М. Хеннесси, Р. Милнер, Алгебраические законы недетерминизма
и параллелизма, J. Assoc. Comput. Mach., 32 (1985), стр. 137–161.
[15] A. Ing´
olfsd´
ottir, J.К. Годскесен и М. Зиберг, Fra
Hennessy-Milner logik til CCS-processing, магистерская диссертация, факультет компьютерных наук
, Ольборгский университет, 1987. На датском языке.
21
Стиль логотипа компьютерных наук, часть 3, часть 1: Теория автоматов
Стиль логотипа компьютерных наук, часть 3, часть 1: Теория автоматов Стиль логотипа компьютерных наук том 3: Помимо программирования 2 / e Copyright (C) 1997 MIT Программный файл для этой главы: fsm
Как я объяснил в предисловии к первому тому, одна из моих целей в написание этой серии книг было призвано отвлечь компьютерных любителей от взгляд на компьютерный опыт как на знание неясных характеристик какого-то конкретного компьютера — как его программировать на машинном языке, что магические числа можно найти где в его памяти, как побороть копию схемы защиты на его дисках и тд.Проблема с такого рода машинно-ориентированный опыт состоит в том, что он устаревает, когда ваш любимый компьютер делает. С моей точки зрения, одно из достоинств логотипа как язык программирования заключается в том, что его структуры данных высокого уровня направляют ваши внимание от вопросов о том, что происходит где в памяти, позволяя вам вместо этого сосредоточиться на более абстрактном описании вашей проблемы.
Теория автоматов — еще один шаг в отвлечении вашего внимания от любых конкретный вид компьютера или конкретный язык программирования.В автоматах В теории мы рассматриваем математическую модель вычислений. Такая модель лишает вычислительную технику — «язык программирования» — до минимум, чтобы легко манипулировать этими теоретические машины (таких моделей несколько, для разных целей, как вы скоро увидите) математически, чтобы доказать свои способности. По большей части, эти математические модели не используются для практических задач программирования. Реальные языки программирования намного удобнее использовать.Но само гибкость, которая упрощает использование реальных языков, также усложняет их говорить формально. Урезанные теоретические машины предназначен для изучения математически.
Что такое математическая модель? Вскоре вы увидите один, который называется «конечный автомат».
Суть данного исследования заключается в том, что математические модели в некоторых важные способы, эквивалент реальным компьютерам и реальному программированию языков. Это означает, что любая проблема, которую можно решить на реальном компьютер может быть решен с использованием этих моделей, и наоборот.Все, что мы можем Доказательство о моделях проливает свет на реальные проблемы компьютера программирование тоже.
Теория автоматов задает следующие вопросы: Есть ли какие-нибудь проблемы, которые не может решить ни один компьютер, независимо от того, сколько времени и памяти он имеет? Может ли доказать , что конкретная компьютерная программа действительно решит конкретную проблему? Если компьютер может использовать два разные внешние устройства хранения (диски или ленты) одновременно, расширяет ли это спектр задач, которые он может решить по сравнению с машина только с одним таким устройством?
Есть также более крупный вопрос, скрывающийся за предысторией автоматов. теория: решает ли человеческий разум проблемы так же, как компьютер делает? Подвержены ли люди тем же ограничениям, что и компьютеры? Теория автоматов на самом деле не дает ответа на этот вопрос, но идеи теории автоматов может помочь в поиске ответа.Подробнее об этом мы расскажем в главе об искусственном интеллекте.
Что такое вычисления?
Какие проблемы мы можем дать нашим абстрактным компьютерам? В теории автоматов мы хотим сосредоточить наше внимание на самих вычислениях, не на деталях устройств ввода и вывода. Поэтому мы не будем пытаться создавать математическая модель видеоигры.
А вот поиграем в игру. В этой игре компьютер имеет в виду правило.
Вы вводите строки букв, используя только буквы A , B и С .Компьютер сообщает вам, соответствует ли каждая строка правилу или
нет. Ваша задача — угадать правило. Например, предположим, что вы сделали
эти эксперименты:
| принято | отклонено |
|---|---|
ABC | CBA |
AAA | BBB |
ABCABCABC | BCABCABC |
A | BBBBBBB |
ACCCCCCCCC | CAAAAAAAAA |
Из этих примеров можно догадаться, что правило
«Строка должна начинаться с A .»Сделав предположение, вы сможете
проверьте это, попробовав больше примеров.
Программа для игры называется game . Требуется один ввод,
число от 1 до 10. Я привел десять различных правил. Правила с 1 по 3
должно быть довольно легко угадать; правила с 8 по 10 должны быть почти невозможными.
(Не расстраивайтесь, если вы их не получите.)
Строка может быть любой длины, включая нулевую (пустая строка). Каждый
когда вы набираете букву, программа сообщает,
набранный до сих пор подчиняется правилу.Программа указывает, является ли строка
принято или отклонено, отображая слово принять или отклонить на
экран. В частности, как только
при запуске игры программа сообщит вам, пустой ли
строка принимается этим правилом. Если вы наберете строку ABC , вы
На самом деле будет тестировать три строки: A, , AB, и ABC, . Ты
следует вводить по одной букве за раз, чтобы программа могла
ответьте на него, прежде чем перейти к следующему письму.Чтобы начать сначала с
другую строку, нажмите клавишу Return.
Вы должны прекратить читать сейчас и попробовать игру. В следующих параграфах Я собираюсь рассказать о некоторых ответах, так что это ваш последний шанс. После того, как вы выяснили хотя бы некоторые правила, приходите вернуться к книге.
Конечные машины
Смысл изучения этой игры в том, что мы собираемся найти способ разработки абстрактный компьютер специального назначения, который понимает один конкретный правило.Затем мы можем задать вопросы о том, сколько информации компьютер нужно справиться с работой.
Вы уже видели слово состояние в связи с логотипом
черепаха. Его состояние включает его позицию и его заголовок. Итак, одна черепаха
состояние может быть «позиция [17 82] , заголовок 90 ». В принципе,
черепаха имеет бесконечных возможных состояний, потому что ее
позиция и заголовок не обязательно должны быть целыми числами. Его позиция может быть [14.142 14.142] , например.
Все, что содержит информацию, может находиться в разных состояниях. Как другой Например, выключатель света имеет два состояния. Некоторые лампы имеют четыре состояния: выкл., низкий, средний и высокий. Компьютер тоже имеет определенное количество состояний. Состояние компьютера включает в себя всю информацию в его памяти в какой-то момент. определенное время.
Машина с ограниченным числом состояний, как в примере выключатель света, называется конечным автоматом . Практически для всех в этой главе мы будем иметь дело с конечными автоматами. Ты можешь подумать что это налагает очень жесткие ограничения на виды вычислений, которые мы можем делать. Но обратите внимание, что в игре, в которую я просил вас сыграть, правило может принимать бесконечное количество возможных строк и отклонить бесконечное количество другие. Принятые или отклоненные строки могут быть любой длины. (Некоторые правила ограничивают длину строки, но другие допускают любую длину вообще.) в некотором смысле, конечный автомат все еще может выполнять бесконечно разные вычисления.
Рассмотрим для примера третью игру. Правило: «Принять
любая строка, которая начинается с AB . «Вот изображение конечного состояния
машина, которая реализует это правило:
Каждый пронумерованный кружок представляет состояние. В этой машине три
состояния. Стрелка start указывает, что машина запускается в состоянии
1. Состояние 3 показано двойным кружком , чтобы указать, что это принимает состояние . Другими словами, когда автомат находится в состоянии 3,
экран говорит, что принимает .Два других государства не
принимающие государства.
Каждый раз, когда вы вводите символ, машина переключается из одного состояния в другое.
еще один. Стрелка из состояния 1 в состояние 2 имеет A рядом с его
хвост. Это указывает на то, что когда автомат находится в состоянии 1, ввод переключает его в состояние 2. (Стрелка из состояния 3 на себя имеет
три буквы ABC на его хвосте. Это сокращенное обозначение
три отдельные стрелы с острием и хвостом в одном месте, по одной для каждой
письмо.)
На самом деле изображение неполное. Полное описание машины
мы должны указать, что происходит на любом входе в любом состоянии. Другими словами,
из каждого круга должно выходить три стрел, по одной
для A , B и C . Я решил принять соглашение, что
каждая машина имеет немаркированное состояние, называемое отклонить . Любая отсутствующая стрелка
переходит в это состояние; как только машина находится в состоянии отказа, она остается
там навсегда.Итак, вот полная схема автомата для игры.
3:
С этого момента я не буду рисовать состояние отклонить , но вы должны
помните, что это действительно часть описания машины. Итак, эта машина
требуется четыре состояния, а не три.
Если первая введенная буква не A , машина переходит к reject государственный. Если первая буква — A , машина переходит в состояние 2. Затем,
если вторая буква B , машина переходит в состояние 3 и принимает
строка AB .Это самая короткая допустимая строка.
Каждая из трех стрелок из состояния 3 возвращается обратно в состояние
3 сам. (Помните, что хотя на картинке изображена только одна стрелка,
он обозначен тремя буквами, так что официально он представляет собой три
стрелки.) Это означает, что когда машина находится в состоянии 3, она остается
там, независимо от того, какие входы он получает. Любая строка, начинающаяся с AB , является
приемлемо.
Вот автомат для игры №2:
В этой машине начальное состояние также является принимающим государственный. (Каждая машина имеет ровно одно начальное состояние, но может иметь любое
количество принимающих состояний.) Эта машина никогда не попадает в отклонение государственный. Это не значит, что он не отвергает никаких строк; все нечетной длины
строки отклоняются в состоянии 2. Но отклоненная строка может искупить себя путем
добавление еще одного входного символа, поэтому состояние 2 позволяет вернуться к принимающему
состояние 1.
Вот автомат для игры номер 5. (Заметьте, что я говорю «a машина », а не« машина »; всегда можно спроектировать другие машины, которые следовали бы тому же правилу.)
Вероятно, у вас было больше проблем с открытием правила 5, чем с правилом
2, и требуется больше времени, чтобы сказать правило английскими словами. Но , машины по двум нормам практически идентичны. (Помните,
хотя, что машина с правилом 5 действительно имеет третье состояние, отклоняет состояние, которое не показано на схеме.)
Вот машины для правил 7 и 9. С этими машинами в качестве подсказок,
ты можешь разобраться в правилах? Вернитесь к программе game для тестирования
ваши гипотезы.
Вы также должны попрактиковаться в переводе в другом направлении, с
Английские правила машинных диаграмм. Вот пара, над чем стоит поработать: Правило 4:
«Чтобы быть принятой, строка должна состоять из удвоенных букв ( AA , BB и CC ), соединенные вместе. Правило 8:
строка должна содержать четное число A s. »
Недетерминированные машины
Вот правило 6: «Чтобы строка была принята, она должна начинаться с A и заканчиваться
с C .»Строки, принятые этим правилом, включают AC (самый короткий
возможно), ABC , AACC , ACAC , ABCABC и т. д.
Между начальным A и последним C принятая строка может
иметь любую комбинацию A s, B s и C s. Это естественно для
представьте, что строка состоит из трех частей: фиксированное начало, переменная
средний и фиксированный конец. Три части входных строк могут быть
удобно представлены в машине тремя состояниями, например:
Машина запускается в состоянии 1.Чтобы быть принятым, строка должна начинаться
с A . Следовательно, стрелка A ведет из состояния 1 в состояние 2. Любое
другой вход в состоянии 1 приводит к состоянию отклонения .
Когда машина находится в состоянии 2, она готова к средней части Струна. В этой средней части допускается любое сочетание букв. Следовательно, есть три стрелки от состояния 2 к самому себе, одна для всевозможные буквы.
Наконец, стрелка C ведет из состояния 2 в состояние 3, сигнализируя об окончании
допустимой строки.Чтобы строка была принята, строка должна заканчиваться на C .
Проблема с этим станком: две стрелки C вывод из состояния 2. Первый — это цикл, возвращающийся в состояние 2; другой
переходит к состоянию 3. Эта ситуация отражает тот факт, что C обслуживает
две разные функции в этом правиле: C — необязательная часть
средняя часть строки, а также обязательный окончательный ввод
в строке.
Машина с двумя стрелками из одного состояния для одного и того же входа назвал недетерминированной машиной .Вот как такая машина может работать: если есть два варианта выбора машины текущее состояние и ввод, машина клонирует себя. Один из экземпляров следует за каждой стрелкой. С этого момента, если либо машина находится в Принимающее состояние строка принята.
Недетерминированные конечные автоматы сложнее чем детерминированные. «Покупает» ли добавленная сложность какие-либо добавленные мощность? Другими словами, может ли недетерминированная машина решать задачи что детерминированная машина не может? Получается, что ответ на этот вопрос нет.Детерминированные машины столь же мощны как недетерминированные. Это важная теорема для автоматов. теория. Я не собираюсь доказывать это формально в этой книге, но проиллюстрирую теорема, вот детерминированная машина, которая выполняет игру 6:
Эта машина похожа на недетерминированную версию. Он имеет одинаковое количество состояний и некоторые соединения идентичны. Однако состояние 3 более сложное. Также в этой машине больше не тот случай, когда каждое состояние машины точно соответствует к одной из трех частей входной строки.В частности, когда машина в состоянии 3 строка может заканчиваться, а может и не заканчиваться.
Представление машин в виде списков логотипов
Игра Программа использует конечные автоматы для представления правил
с помощью которого он принимает или отклоняет строки. (Машины должны быть детерминированными
чтобы программа работала.) Программы с логотипом не могут читать круги и стрелки,
Итак, машина представлена в виде списка. Какая информация есть на самом деле
содержится в диаграмме конечного автомата? На диаграмме видно, что существуют определенные
количество состояний (кружки), что есть определенные переходы из одного
состояние к другому (стрелки), что одно конкретное состояние является начальным состоянием
(стрелка начала), и что определенные состояния принимают их (двойная
круги).Как и в любом программном проекте, я мог выбрать много разных
способы представления этой информации в программе.
В выбранном мной конкретном представлении список машины состоит из трех членов. Первый член — это номер начального состояния. Второй член — это список стрелок; каждая стрелка сама по себе является списком, как я объясню через мгновение. Третий член списка машин — список принимающих состояний машины. Например, здесь это снова машина для игры 3, в обеих формах:
[1 [[1 A 2] [2 B 3] [3 ABC 3]] [3]]
Число 1 — начальное состояние; список [3] — это
список принимающих состояний.(У этой машины есть только один принимающий
состояние.) Все остальное — список стрелок. Каждая стрелка — это тоже список
с тремя членами: начальное состояние (хвост стрелки), вход
буква или буквы и конечное состояние (острие стрелки). Первая стрелка в
эта машина
[1 A 2]
Это стрелка из состояния 1 в состояние 2, связанная с
вход А .
Список [3 ABC 3] в этом аппарате представляет три стрелки, используя
такое же сокращение, как на диаграммах со стрелками и кругами.Я мог в равной степени
хорошо изобразили эти стрелки по отдельности:
[1 [[1 A 2] [2 B 3] [3 A 3] [3 B 3] [3 C 3] ] [3]]
Как и на диаграммах со стрелками и кругами, я не представлял явно
переходы в состояние отклоняют состояние в этих списках. Программа
написано так, что если он не находит переход для текущего состояния и
вход в список переходов, он переходит в состояние с номером -1, его
представление для отклонить состояние .
Вот еще несколько списков машин:
Игра 2: [1 [[1 ABC 2] [2 ABC 1]] [1]] Игра 7: [1 [[1 AB 1] [1 C 2] [2 C 1]] [1]] Игра 9: [1 [[1 AB 1] [1 C 2] [2 A 3] [2 B 1] [3 A 1]] [1]]
На этом этапе вы должны остановиться и поиграть с программой. Макияж, мириться
свои собственные правила. Процедура fsm принимает список машин в качестве входных данных.
и принимает строки на основе этой машины. ( Game использует fsm с особым
машины в качестве входных данных.) Попробуйте свои новые правила, чтобы убедиться, что вы разработали
машины правильно.Затем попросите друга поиграть по вашим правилам.
Если вы оба читаете эту книгу вместе, вы можете устроить соревнование.
(Легко разработать правила, которые невозможно угадать, потому что
слишком много деталей. Если у вас есть соревнование, вы должны ограничить
до трех состояний на машину.)
Возможно, вам будет интересно прочитать программа fsm , которая
имитирует конечный автомат, когда дано описание машины
как его вход. Это довольно простая программа.Если вы думаете о машине
диаграмма состояний как своего рода «электрическая схема», которую можно использовать
при создании реальной версии этой конкретной машины эта программа Logo
это своего рода реализация универсального конечного автомата .
Текстовые редакторы: использование акцепторов
Вам может показаться, что принятие или отклонение строк — это не так уж и много как то, что вы обычно делаете с компьютерами. Вы можете спросить, как это Математическая модель связана с реальным компьютерным программированием. Там два ответа на этот вопрос.Во-первых, можно спроектировать конечные автоматы, которые имеют более универсальные выходы, чем просто да или нет. Вскоре я приведу пример. Но другой ответ что есть реальные ситуации, когда принятие или отклонение строки символов действительно возникает в практических вычислениях.
Один из примеров — реализация языков программирования. Когда Вы говорите, что
печать 2 + 2
— это официальная инструкция для логотипа, но
печать 2+
является незаконным, вы делаете более сложную версию того, что акцептор с конечным состоянием делает.
Команда search в хорошем текстовом редакторе использует конечные автоматы. В большинстве текстовых редакторов есть команда, позволяющая вы можете просмотреть файл в поисках определенной строки символов. Любитель редакторы позволяют искать не только одну строку, но и любую строка, которая следует правилу, которое может предоставить пользователь. Редактор находит строку, соответствует правилу с использованием конечного автомата. Конечно, люди, использующие редакторам не нужно указывать свои правила поиска в форме конечный автомат! Программа редактирования принимает правила поиска в более простом виде. form и переводит их в форму FSM.Вот пример, обозначение используется ed, — стандартным редактором в операционной системе Unix.
Строка типа
спагетти
просто соответствует идентичной строке в файле, который вы редактируете. А немного более интересный случай
[Ss] paghetti
, что соответствует либо «спагетти», либо «спагетти». (с заглавной или строчной буквы «s»). Квадратные скобки означают, что Принимаются любые букв внутри скобок.В выражении
[Ss] paghet * i
звездочка соответствует любому номеру (включая ноль)
письмо перед ним (в данном случае буква т ). Этот пример
будет соответствовать любому из них:
Спагей Спагеттти спагетти спагети
Вы можете использовать это в поисковой команде, если плохо пишете! Скобу и звездочку можно комбинировать;
C [AD] * R
будет соответствовать любому из
АВТОМОБИЛЬ CDR CADDR CR
Или вы можете использовать
M [is] * p * i
, чтобы соответствовать названию известной реки.
Некоторые правила из игры, которую я представил ранее, можно представить в виде ed поисковые строки в соответствии с этими правилами. В первой игре
машина принимает любую строку, состоящую из A, s и B s. В
соответствующее выражение ed
[AB] *
В третьей игре используются строки, начинающиеся с последовательности AB , а затем все, что угодно. Это можно представить как
AB [ABC] *
Игра 10, которую, я уверен, вы не решали, принимает любую строку,
включает в себя последовательность ABCBA .В терминах ed это
[ABC] * ABCBA [ABC] *
Я не дал вам полного описания правил поиска ed . Я включил это только потому, что хочу, чтобы вы увидели, как «настоящая» программа использует идею конечных автоматов. Но в остальной части этого Глава Я хочу использовать другую нотацию, основанную на словах и списках логотипа.
Регулярные выражения
Обозначение, которое я собираюсь описать, допускает правило принятия, как и правила
в программе game или правилах поиска ed , чтобы
представлен в логотипе.Представление такого правила называется регулярное выражение. Я расскажу вам несколько правил о том, что
выражение может выглядеть. Не путайте: любой конкретный регулярный
выражение — это правило, которое принимает строки букв. Я даю вам правила
которые принимают регулярные выражения — правила о правилах. В качестве грубой аналогии
«размер одного игрока X , а другого O » — это правило
специфическая игра Tic Tac Toe; «у каждого игрока должен быть шанс на победу»
это правило о том, какие правила игры приемлемы.
Алфавитная линейка. Любой символ в машинном
алфавит — это регулярное выражение. Представляем символ однобуквенным
Слово логотипа. В нашей игре в угадайку алфавит состоит из трех символов: A , B и C . Так
B
— регулярное выражение.
Правило конкатенации. Список, члены которого являются регулярными выражениями.
представляет эти выражения одно за другим. Например, начиная с A — регулярное выражение, а B — регулярное выражение,
[A B]
— это регулярное выражение, представляющее строку AB .(Уведомление
что слово логотипа AB не , а представляет эту строку; то
правило алфавита требует, чтобы каждая буква была представлена как отдельное слово.)
Правило альтернатив. Список, первым членом которого является слово или и
остальные члены которой являются регулярными выражениями, представляют любую строку,
соответствует любым из этих выражений. Например,
[ИЛИ [A A] B]
соответствует либо последовательности AA , либо одиночному символу B .Для удобства слово логотипа, содержащее более одной буквы (другие
чем слово или ) рассматривается как сокращение для или ing
отдельных букв. Например, ABC эквивалентно [OR A B C] .
Правило повторения. Список, содержащий ровно два элемента, в которых
первый — символ звездочки ( * ), второй — обычный
выражение, представляет собой строку, содержащую любое количество (включая ноль)
подстроки, соответствующие регулярному выражению.Так
[* [ИЛИ [A A] B]]
соответствует любому из этих:
B |
BB |
BAAB |
AAAAAA |
AABAA |
| (пустая строка) |
AABBBBBAA |
Число последовательных A s должно быть четным для строки A s и B s, чтобы соответствовать этому выражению.
Эти четыре правила составляют определение регулярного выражения. Это рекурсивное определение . Так же, как эффект рекурсивного Процедура создания логотипа определяется в терминах более простого случая той же процедуры, сложное регулярное выражение определяется в терминах более простых.
Вот десять правил игры из начала этой главы в форма регулярных выражений:
| 1. | [* AB] |
|---|---|
| 2. | [* [ABC ABC]] |
| 3. | [A B [* ABC]] |
| 4. | [* [ИЛИ [A A] [B B] [C C]]] |
| 5. | [* [ABC B]] |
| 6. | [A [* ABC] C] |
| 7. | [* [OR A B [C C]]] |
| 8. | [[* BC] [* [A [* BC] A [* BC]]]] |
| 9. | [[* AB] [* [C [OR B [A A]]] [* AB]]] |
| 10. | [[* ABC] A B C B A [* ABC]] |
Вам следует внимательно просмотреть эти примеры, убедившись, что вы понимаете, как регулярное выражение представляет ту же идею как в описании на английском языке или на схеме машины, которую вы видели ранее.
Необычные правила
Вы можете подумать, что любое правило для принятия или отклонения строки символов могут быть представлены как регулярное выражение.Но это не так. Например, рассмотрим правила распознавания обычных арифметические выражения:
| принято | отклонено |
|---|---|
2 + 3 | 23+ |
2 * (3 + 4) | 2 *) 3 + 4 ( |
-5 | /6 |
Задумайтесь на мгновение о том, балансирующие скобки.Иногда круглые скобки заключаются в круглые скобки, как в
((3 + 4) / (5 + 6))
Как бы вы изобразили эту часть арифметического выражения? правило в виде регулярного выражения? Вы не можете просто сказать что-то вроде
[[* (] что-то или другое [*)]]
означает «любое количество открытых скобок, что-нибудь, тогда любое количество закрывающих скобок ». Это позволит строкам вроде
(((7)))))
Но эту строку следует отклонить, потому что в ней слишком много близких скобки.Вам не разрешается использовать закрывающую скобку, если вы не уже использовал подходящую открывающую скобку. Вы можете иметь любое количество вложенных круглые скобки, если они сбалансированы.
Можно изобрести другие виды формальных обозначений, более мощные, чем
регулярные выражения, которые позволят нам дать правила для правильно сформированных
арифметические выражения. В этом разделе я кратко представлю формальную
обозначение под названием производственные правила , достаточно мощное, чтобы описать
арифметические выражения.Сейчас в этой главе я не хочу обсуждать
детально проработанные правила производства; моя единственная причина представить их на
этот момент должен дать вам представление о том, как регулярные выражения вписываются в
большая вселенная возможных формальных систем. В следующих разделах я
есть что сказать о регулярных выражениях и конечных автоматах. Но
мы вернемся к правилам производства в главах 5 и 6, в которых нам понадобится
формальные обозначения, с помощью которых можно обсуждать более интересные языки, чем A — B — C язык данной главы.(В главе 5 мы будем
говорить о Паскале; в главе 6 мы займемся английским языком.)
Ключевой компонент, отсутствующий в нотации регулярных выражений, — это способ до имя своего рода подвыражение, чтобы имя можно было использовать в определение более сложных выражений. В частности, имя подвыражения может использоваться в собственном определении, чтобы разрешить рекурсивное определение правило.
Производственное правило имеет вид
название: расширение
Каждое правило представляет собой определение имени слева в терминах меньшие единицы, аналогично определению процедуры логотипа в терминах подпроцедур.Раскрывающая часть правила представляет собой строку символов. включая оба члена «алфавита» системы (например, алфавит который лежит в основе языка регулярных выражений) и имен, определенных правила производства.
В качестве примера приведем набор производственных правил, определяющих язык арифметические выражения. Эти правила учитывают «порядок операции «для арифметики, которую вы изучали в начальной школе: умножение перед сложением. Выражение вроде
2/3 + 1/6
обычно интерпретируется как сумма двух членов , а именно две трети и одна шестая.Выражение может быть одним членом, суммой термины или разница в сроках. Вот как эта идея выражается в наборе правил производства; Я расскажу об обозначениях более подробно чуть позже.
Вертикальные полосы разделяют альтернативы. Первое правило, единственное
который определяет expr , содержит три альтернативы. Во-первых, выражение
может быть всего лишь одним термином. Во-вторых, выражение может быть меньшим
выражение плюс термин. В-третьих, выражение может быть выражением меньшего размера
минус срок.Символы внутри прямоугольников являются членами алфавита
язык арифметических выражений. (Я положил их в коробки, чтобы
их проще не путать с знаками препинания — двоеточиями и
вертикальные полосы — это часть самой нотации производственного правила.)
Вы видите, как подходят круглые скобки? Если строка типа 4 + 5 является
выражение, то (4 + 5) — коэффициент, поэтому 3 * (4 + 5) — член,
и так далее. Поскольку фактор — это разновидность термина, а термин — разновидность
выражение, множитель (4 + 5) можно рассматривать как выражение, и
поэтому его тоже можно заключить в круглые скобки.Таким образом, ((4 + 5)) также
приемлемый как фактор.
Регулярные выражения и конечные автоматы
Я намекнул на то, что на самом деле не сказал явно: Обычный выражения эквивалентны конечным автоматам. Другими словами, если вы можете выразить правило в виде регулярного выражения, вы можете создать конечный автомат, который выполняет это правило. Если ты не можешь писать регулярное выражение для правила, вы не можете создать конечное состояние машины тоже нет.
Вы можете подумать «ну и что?» Я представил два разных формальных нотации, конечные автоматы и регулярные выражения, и теперь я говоря вам, что эти два эквивалента.Так почему я просто не выбрал один первое место и забыть о другом? У меня есть общий ответ и конкретный ответ на эти вопросы.
Общий ответ таков: сравнение различных формальных систем — вот что теория автоматов — это все. К концу этой книги вы будете познакомился с полдюжиной различных формальных систем. Некоторые больше сильнее других. Простое утверждение, что одна формальная система эквивалентен другому или более мощный, чем другой, не очень интересен; но если мы сможем понять причин , стоящих за этими утверждениями, тогда возможно, мы сможем применить знания на практике.На в самом конце этой книги, в главе 6, мы поговорим об особом формальном система, которая часто используется в программах искусственного интеллекта для распознавания Английские предложения. К тому времени вы должны знать достаточно о формальных системах, чтобы уметь понять, почему именно этот вариант — хороший выбор.
Конкретный ответ заключается в том, что конечные автоматы и регулярные выражения отличаются друг от друга интересным образом. Конечное состояние машина — это алгоритм , — последовательность шагов или процедура, которая может следовать, чтобы проверить, соответствует ли некоторая строка заданному правилу.Он говорит: «начни здесь, затем, если это произойдет, сделай это, тогда …» как процедура в Logo или большинстве других языков программирования. (Но мы видели, что конечный автомат похож на процедуру, написанную в ограниченном программировании язык, который не так гибок, как Logo.) Однако регулярное выражение , а не , последовательность шагов. Это больше похоже на описание результат , который мы хотим, оставив открытым точный рецепт, как этого добиться. Люди часто создают проблемы подобным образом.Они вызывают сантехника и говорят: «сток в моей ванне идет обратно». Часть опыта водопроводчика чтобы иметь возможность перевести декларативную формулировку проблемы в процедурная форма , последовательность шагов, необходимых для устранения проблемы. Первым камнем преткновения в исследованиях искусственного интеллекта было кажущееся пропасть между процедурными знаниями, воплощенными в компьютерной программе, и декларативные знания, необходимые для человеческого поведения. В последнее время у людей есть изобрел декларативных языков программирования (самый известный это Prolog, но любая коммерческая программа для работы с электронными таблицами также в этой категории), что позволяют пользователю заявить о проблеме в декларативной форме.Программирование языковой интерпретатор автоматически переводит эту постановку задачи в последовательность шагов, которые должен выполнить компьютер.
Написание интерпретатора Пролога поднимает много вопросов, выходящих за рамки данной статьи.
книга. Но мы можем сделать меньший шаг в области перевода с
декларативное обозначение к процессуальному. Я написал программу с логотипом,
перечислены в конце главы, что переводится с обычного
выражение в эквивалентный конечный автомат. Его процедура верхнего уровня, машина , принимает регулярное выражение в качестве входных данных и выводит машину
список в формате, который я показал ранее.
Как перевести
Общее утверждение, что регулярные выражения эквивалентны по мощности для конечных автоматов называется теоремой Клини, названной в честь математик Стивен К. Клини, его первооткрыватель. Вы можете найти доказательство этой теоремы в любом учебнике по теории автоматов. я не собираюсь чтобы дать здесь доказательство, но я укажу, как делается перевод в моей программе. В доказательстве используются те же идеи.
Помните, что определение регулярного выражения состоит из четырех частей.Правило алфавита обеспечивает фундаментальные строительные блоки; то
конкатенация, альтернативы и правила повторения создают большие регулярные
выражения рекурсивно из более мелких. Процесс перевода
следует тому же шаблону: мы начинаем с процедуры построения тривиального
машина с двумя состояниями, которая принимает только одну букву, затем мы добавляем три
правила объединения машин меньшего размера в большую машину. В следующих
абзацев, я покажу, как каждое правило отражается в машина программа.
Этот процесс строительства часто производит машины с большим количеством состояний, чем
необходимо. Программа машины устраняет избыточные состояния как ее
Заключительный этап.
Правило алфавита гласит, что любой член алфавита машины
регулярное выражение. В программе символом может быть любое однобуквенное слово другое
чем * . Обозначение X переведено на автомат.
[1 [[1 X 2]] [2]]
(Вы увидите, что программа работает, комбинируя маленькие машины
в более крупные.Каждый раз программе приходится изобретать новую машину
указать, что он использует следующий свободный номер. Значит, государственные номера могут не
быть 1 и 2 в реальном примере.) Процедура ndletter справляется с этим
правило.
Затем следует правило конкатенации . Регулярное выражение
[A B]
соответствует строке из двух частей; то
первая подстрока соответствует A , а вторая соответствует В . В этом простом примере каждая «подстрока» соответствует только одному
письмо.В более сложной конкатенации, например
[[OR A C] [* B]]
есть разные варианты выбора для каждой подстроки. Например, что регулярное выражение соответствует строке
CBBB
, в котором буква C соответствует первой части
выражение и подстрока BBB соответствует второй части.
Чтобы преобразовать регулярное выражение такого типа (конкатенацию) в
конечного автомата, мы начинаем с рекурсивного перевода подвыражений
на более мелкие машины.Затем мы должны «соединить» две машины вместе.
Процедура ndconcat выполняет это соединение.
Начнем с самого простого примера. Предположим, мы хотим переведите регулярное выражение
[A B]
Мы уже перевели два символа A и B в
машины:
Комбинированная машина должна запускаться в состоянии запуска первого составная машина, состояние 1. Комбинированная машина должна находиться в приемном состояние, когда оба компонентов машины удовлетворены; в другом словами, принимающие состояния комбинированной машины должны быть вторая машина компонентов.В данном случае это означает только состояние 4.
Чтобы соединить компоненты машин вместе, мы должны добавить переходы (стрелки)
между ними. В частности, всякий раз, когда первая компонентная машина попадает в
состояние приема, комбинированная машина должна следовать тем же переходам
которые применяются к начальному состоянию второй компонентной машины. В этом
случай, когда комбинированная машина переходит в состояние 2 (принимающее состояние
первый компонент машины) он должен следовать тем же переходам, что и
применяются к состоянию 3 (начальное состояние второй машины).Здесь только один
такой переход, стрелка B в состояние 4. Это означает, что мы должны добавить
стрелка
[2 B 4]
к комбинированной машине.
Состояние 3, хотя оно все еще находится в машине, сейчас бесполезно. Машина не может перейти в состояние 3. Позже в процессе перевода другая процедура удаляет такие «осиротевшие» состояния от машины.
В качестве немного более сложного примера рассмотрим перевод регулярное выражение
[[OR A C] [* B]]
Начнем с предположения, что мы уже перевели два подвыражения отдельно:
(Мы еще не обсуждали правило альтернатив или повторение правило, поэтому я еще не объяснил, как переводятся эти подвыражения.А пока поверьте, что это изображение правильное. Мы получим к этим другим правилам в ближайшее время.)
Начальное состояние комбинированной машины — это начальное состояние первого компонент, состояние 1. В каждом состоянии принятия первой машины мы должны продублируйте переходы из начального состояния второй машины. В в этом примере начальное состояние второй машины имеет только переход
[4 B 5]
, но на первой машине есть два состояния приема, поэтому мы необходимо добавить две новые стрелки:
[2 B 5] [3 B 5]
Последняя деталь заключается в том, что в этом примере начальное состояние второй компонентный автомат, состояние 4, является состоянием приема.Это означает, что вторая подстрока может быть пустой. Поэтому принимающие состояния машина первого компонента также должна принимать состояния комбинированного машина. Вот результат:
Опять же, состояние 4 теперь «сирота» и будет устранено. позже в программе.
Правило альтернатив объединяет две машины параллельно, так сказать,
а не сериями. Он работает, изобретая новое состояние
это становится начальным состоянием комбинированной машины. Стрелки уходят
из нового состояния продублируйте стрелки из начальных состояний
комплектующие машины.Процедура ndor обрабатывает это правило.
В качестве примера приведем процесс перевода для
[OR A B]
(или его аббревиатура AB ). Начнем с двух отдельных машин:
Мы объединяем их, изобретая новое состояние 5:
Я не объяснил все детали процесса строительства. Например, должно ли новое состояние, состояние 5, быть принимающим? В этом пример быть не должно. Посмотрите, сможете ли вы придумать случай, в котором это могло бы быть; затем прочтите листинг программы, чтобы увидеть точный алгоритм, который делает это решение.Опять же, этот процесс построения может оставить неиспользуемые состояния на позже уборка.
Гораздо более серьезная проблема заключается в том, что конструкция или может
произвести недетерминированную машину. Например, вот машина
за
[ИЛИ [A B] [A C]]
Подобно неиспользованным состояниям, проблема недетерминизма
осталось до конца программы, когда процедура определяет, что переводит
недетерминированную машину в детерминированную.
(Правило конкатенации также может создавать недетерминированные машины, хотя
это не так вероятно.)
Последний случай, который необходимо рассмотреть, — это правило повторения . Это правило
действует только на одну машину меньшего размера, а не на две машины, как в предыдущем
два случая. Правило не требует никаких новых состояний. Он имеет два эффекта.
Один из них — добавить начальное состояние в список принимающих состояний. В
во-вторых, добавить стрелки из (старых) принимающих состояний, которые имитируют
стрелки из начального состояния. (Это в точности похоже на сращивание
двух машин в правиле конкатенации, но в этом случае мы конкатенируем
одна машина сама с собой!) Порядок действий ндманы делает это преобразование.Это тоже может привести к недетерминированной машине.
Вот пример правила:
Эти четыре правила объединены nondet ,
процедура, вход которой
регулярное выражение, вывод которого — машина (возможно, недетерминированная).
для nondet: regexp if и (wordp: regexp) (equalp count: regexp 1) [output ndletter: regexp] если wordp: regexp [вывод ndor сокращение "предложение: regexp] если сначала равно: regexp "или [output ndor butfirst: regexp] если равняется сначала: regexp "* [вывод ndmany last: regexp] вывод ndconcat: regexp конец
Процедура верхнего уровня машина делает небольшую инициализацию
а затем выполняет свою работу по инструкции
оптимизировать вывод определить nondet: regexp
То есть сначала он создает то, что может быть недетерминированная машина затем, если необходимо, он переводит это в детерминированный (исключая сиротские состояния в процессе), то он получает Избавьтесь от любых избыточных состояний, которые могли быть созданы.
Делаем машину детерминированной
В первом томе этой серии мы исследовали технику поиска в глубину. и обход дерева в ширину. Учитывая древовидную структуру, эти алгоритмы позволяют нам «посетить» каждый узел дерева один раз.
Конечный автомат можно рассматривать как структуру почти как дерево. Начальное состояние машины соответствует корневому узлу; заявляет, что могут быть достигнуты стрелкой из данного состояния, являются дочерними элементами этого состояния.Но есть одно важное различие между деревьями и машинами: на дереве у каждого узла (кроме корневого) есть ровно один родитель. Дерево алгоритмы поиска зависят от этого факта, чтобы гарантировать, что каждый узел посещен только однажды. В машине стрелки из нескольких разных состояний могут привести к одно и то же государство, поэтому у государства может быть несколько «родителей». Техническое название для произвольного набора узлов со связями между ними является график. Если соединения односторонние, как в конечном диаграммы состояний, это называется ориентированным графом .
Поиск в графе похож на поиск в дереве, за исключением того, что мы должны
отслеживать, какие узлы мы уже посетили, чтобы не проверять
один и тот же узел дважды. Процедура определения создает список с именем состояний , первоначально
пустой, в который каждый номер состояния добавляется как
программа исследует это состояние. Глубина первого обхода станка
осуществляется по процедуре nd.traverse ;
хотя эта процедура выглядит иначе, чем глубина.первый процедуры в томе 1, это
использует тот же базовый алгоритм. Учитывая состояние в качестве входных данных, он обрабатывает
это состояние и рекурсивно вызывает себя для всех дочерних элементов
это состояние — состояния, достижимые стрелками из состояния ввода. В отличие от depth.first , а nd.traverse — это операция. Это
выводит новый список ходов (стрелки) для детерминированной версии
машина.
Что означает обработка состояния? Nd.traverse первые проверки
было ли это состояние уже обработано; если это так, он выводит пустой
list, потому что это состояние не будет вносить никаких новых ходов в машину.В противном случае он запоминает этот номер состояния как обработанный, находит
все ходы, начиная с этого состояния, и называет check.nd искать
недетерминизм. Check.nd берет первую доступную стрелу, хвост которой
находится в состоянии, которое мы обрабатываем, и ищет все стрелки с одинаковыми
хвост и с той же буквой. * Локальная переменная Heads будет содержать список всех номеров состояний.
достижимые этими стрелками. (Номера состояний отсортированы по возрастанию
порядок, а дубликаты устранены.Если в машине два полностью
одинаковые стрелки, что не приводит к недетерминизму.)
* Кстати
nondet всегда
создает стрелки только из одной буквы; если две или более буквы идут от
одно и то же состояние в одно и то же состояние, отдельная стрелка создается для каждого из
их. Это делает список машин более длинным, но делает такие шаги
один — искать две стрелки с одной и той же буквой — проще. Однажды
Создана детерминированная машина, процедура optimize объединит
такие стрелки в сокращенную форму с
более одной буквы на стрелку.
Есть
три случая, которые должны сделать check.and . Во-первых, если есть
только один государственный номер в : головы , то недетерминизма для
это письмо, а чек. и включает стрелку из оригинала
машина как часть детерминированной машины. Во-вторых, если есть еще
чем один номер штата, проверка и проверяет, видели ли мы уже
та же комбинация состояний результата. Если да, то мы уже создали
новое состояние, эквивалентное этой комбинации старых состояний, и проверка .nd создает новую стрелку, указывающую на это существующее новое состояние. Наконец, третий
Дело в том, что мы не видели такой комбинации состояний раньше. В
В этом случае check.nd должен создать новое состояние со стрелками, дублирующими
те из всех исходных государств.
Другими словами, если есть стрелки
[[3 B 4] [3 B 7]]
, затем check.nd создаст новое состояние, которое является «псевдонимом».
для «четыре и семь». Если на той же машине есть стрелки
[[8 C 4] [8 C 7]]
, затем чек.nd будет использовать то же состояние псевдонима для этого
пара, не изобретая нового. Новый
состояние помечено стрелками, соответствующими стрелкам всех его компонентных состояний (4
и 7 в этом примере). Новое состояние может само содержать недетерминированный
ветвь, но это нормально, потому что новое состояние в конечном итоге будет обработано
по мере продолжения обхода машинного графа.
Вы могли подумать, что этот процесс может продолжаться вечно: каждый новый
состояние чек. и изобретений окажутся недетерминированными, что
потребуется еще одно новое состояние для разрешения.К счастью, это
не бывает; процесс всегда рано или поздно заканчивается. (В следующий
в главе мы увидим, какой лимит на количество необходимых состояний
для детерминированной машины.)
Поскольку определяет, что использует алгоритм обхода графа для проверки
исходные состояния машины, он никогда не найдет «сиротские» состояния
которые не могут быть достигнуты стрелками из другого состояния. Поэтому
процесс создания детерминированной машины также устраняет сирот
состояния, без дополнительных усилий.
Устранение избыточных состояний
Машины, производимые компанией , определяют, что работоспособны, но часто уродливы;
они содержат намного больше состояний, чем необходимо. Процедура оптимизировать устраняет множество избыточностей, а также объединяет стрелки с одинаковыми
голова и хвост, но с разными буквами.
Сначала он просматривает список стрелок машины,
создание списка для каждого состояния, представляющего выходы из этого состояния:
[[* [A B]] C] Состояние 1: [[A 2] [C 4]] Состояние 2: [[B 3]] Состояние 3: [[A 2] [C 4]] Состояние 4: []
В этом аппарате состояния 1 и 3 имеют одинаковый список выхода.(В этих списках каждая стрелка представлена только двумя элементами; хвост стрелы в комплект не входит. Это потому, что состояния 1 и 3 будут не имеют идентичные списки, если были включены хвосты. Список государства 1 было бы
[[1 A 2] [1 C 4]]
и список состояния 3 будут иметь стрелки, начинающиеся с 3. В В программе двухчленная форма стрелки называется заглушкой . )
Программа должна внимательно следить за порядком, в котором она ставит заглушки в списке каждого штата, поэтому он не заканчивается
[[C 4] [A 2]]
для одного из штатов.Вот почему stub.add испытывает проблемы
вставлять каждую заглушку в четко определенную позицию, а не просто добавлять
каждая новая заглушка в начале или в конце списка. Это также в stub.add что стрелки, соединяющие одинаковые два состояния, но с разными
буквы объединены в единую стрелку.
Поскольку состояния 1 и 3 также согласны в своей приемлемости (а именно, они не
принимающие состояния), их можно объединить в одно состояние. Optimize.state может заменить каждую ссылку на состояние 3 ссылкой на
состояние 1.
Сумматор с конечным числом состояний
Я обещал ранее показать вам использование конечных автоматов и других чем принятие или отклонение строк. В этом разделе я выполню это обещание, создавая машину для сложения двух чисел. Мы представим числа в двоичной системе счисления, в которых каждая цифра представляет собой степень вместо 2 вместо 10.
Если вы раньше сталкивались с двоичными числами, можете пропустить этот абзац. Так же, как обычное обозначение чисел основано на десяти цифрах от 0 до 9, двоичная запись основана на двух цифрах , 0 и 1.В обычном («десятичное») обозначение, сумма, которую каждая цифра вносит в общую зависит от того, где он находится в номере. Например, в числе 247 знак цифра 2 дает двести, а не просто две, потому что она находится в третьем отсчет позиции справа. Вклад каждой цифры — это значение сама цифра, умноженная на десять:
2 × 10 2 + 4 × 10 1 + 7 × 10 0(10 2 равно 100; 10 1 равно 10; 10 0 равно 1.) В двоичном формате вклад каждой цифры умножается на степень два, , так что двоичное число 10101 представляет
1 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0что равно 16 + 4 + 1 (2 4 +2 2 +2 0 ) или 21. Компьютеры используют двоичную запись потому что легко построить электрические цепи, в которых каждый провод либо включен или выключен.В главе 2 мы поговорим о примере. Прямо сейчас я хочу показать что-то другое — не настоящую электронную машину, а абстрактную machine на основе идей, которые мы использовали в этой главе.
Машина будет складывать два двоичных числа, по одной позиции за раз, просто как вы сами складываете многозначные числа. Когда вы видите такую проблему, как
вы начинаете справа и говорите: «6 плюс 2 равно 8; 7 плюс 7 равно 14, что 4 переноски 1; 1 плюс 3 плюс 5 равно 9. «Конечный сумматор работает так же. способ, за исключением того, что цифры всегда 0 или 1.
Машина будет складывать любые числа, но чтобы объяснить, как это работает, я хочу рассмотрим конкретный пример. Допустим, мы хотим сложить 52 и 21. (Судя по Кстати, я выбрал эти числа не потому, что они называют карточные игры, а потому, что образец цифр в их двоичной форме удобен для объяснение, которое я хочу дать.) 52 в двоичном формате — это 110100 (32 + 16 + 4), а 21 — это 10101 (16 + 4 + 1). Я напишу это одно над другим, с парой дополнительных нулей слева, чтобы оставить место для возможного переноса:
0 0 1 1 0 1 0 0
0 0 0 1 0 1 0 1
Вспомните, как работает конечный автомат: в данный момент он
в каком-то состоянии , затем он считывает некоторый входной символ и переходит к
другое состояние.В этой задаче, поскольку нам нужно сложить два числа, наиболее
естественный способ подумать об этом — дать машине два входа вовремя. Эта идея не совсем соответствует формальному определению
конечный автомат, но мы можем позволить автомату состоять из пар цифр, поэтому что-то вроде 01 будет одним вводом.
(Кстати, слово бит обычно используется как сокращение для
«двоичная цифра»). Так же, как вы добавили вертикальные пары цифр (первые 6 и 2,
затем 7 и 7 и т. д.) в предыдущем примере мы будем использовать вертикальные пары
биты в качестве входных данных для сумматора с конечным числом состояний, начиная с правого конца.Таким образом, первый ввод будет 01, затем 00, затем 11, затем 00, затем снова 11,
затем 10, а затем дважды 00. С этого момента в этом разделе, когда вы видите
что-то вроде 10, вы должны помнить, что это единственный вход для
конечный автомат, один символ, а не два подряд.
(На схеме ниже стрелка с надписью 01/10 представляет два
стрелки, одна для входа 01 и одна для входа 10 . Эти
две стрелки всегда будут переходить в одно и то же состояние, потому что 0 + 1 = 1 + 0.)
Нам нужно внести одно изменение в обозначения, используемые на схемах машин. Мы больше не хотим отмечать каждое состояние как принимающее (двойной кружок) или отклонение (одиночный кружок). Вместо этого каждое состояние производит выведите , который может быть любым произвольным символом. В этой машине выходы будет 0 или 1, представляя двоичные цифры суммы. Внутри каждый круг штата, вместо номера штата вы увидите что-то как «3/1»; это означает, что это состояние номер 3 и что выход из этого состояния — 1.
Вот машина:
Состояние 1, начальное состояние, не имеет выхода. Когда машина запускается заявить, что он еще не видел никаких цифр в слагаемых, поэтому он не может вычислить цифра суммы. Состояния 2 и 4 выводят нулевую цифру, а состояния 3 и 5 выводят единицу. (Как и входные данные, число, которое машина выходы представлены первым своим крайним правым битом. Машина работает таким образом по той же причине, что и , вы, , складываете числа справа слева: это направление, в котором перемещается цифра «переноса». один столбец в другой.)
Почему два состояния с нулевым выходом и два с одним выходом состояния? Причина в том, что машина находится в состоянии 4 или 5, когда перевод в следующую цифру суммы.
Давайте рассмотрим мой пример. Мы начинаем в состоянии 1. Первый вход символ 01, представляющий 0 в крайнем правом (двоичном) разряде 52 и 1 в крайней правой цифре 21. Машина переходит в состояние 3. и выводит 1.
Следующий ввод — 00, потому что оба числа имеют ноль в качестве второго цифра.Машина переходит в состояние 2 и выводит 0.
Следующий вход — 11. Машина входит в состояние 4 и выдает 0. Находясь в состояние 4 означает, что есть перенос из этой позиции в следующую.
Вы можете закончить пример самостоятельно. Сумма должна быть 01001001, или 73.
Счетные и конечные машины
Ранее мы видели, что вы не можете написать регулярное выражение для правила. это требует сбалансированных скобок. Поскольку регулярные выражения эквивалентно конечным автоматам, вы не удивитесь, узнав что конечные автоматы не умеют считать.
Фактически, они могут считать до определенного момента; просто каждое конечное состояние машина может считать только до фиксированного лимита. Например, вот конечный автомат, который принимает строки сбалансированных круглых скобок до четырех глубин:
Этот аппарат принимает такие строки:
() (()) () ()
(() ()) (((()))) ((((()))) (())
Нет ограничений на длину строки this машина может справиться. Например, он примет это:
() () () () () () () () () () () () () ()
Но открывать может не более четырех круглых скобок сразу ; машина отклонит
((((()))))
Даже эта ограниченная счетная способность конечных автоматов имеет большое значение. практическая ценность.В конце концов, настоящие компьютеры имеют конечное состояние. машины. Любой реальный компьютер имеет ограниченный объем памяти, и это память может находиться в конечном числе состояний. Но число вполне огромный. Если на реальном компьютере есть программа для подсчета скобок это ограничено, скажем, 20 000 уровней скобок, никто не будет когда-нибудь замечаете, что предел не бесконечен.
(количество состояний на реальном компьютере может быть даже больше, чем у вас мышление. Каждый бит компьютерной памяти — это не состояние. Вместо этого, если компьютер имеет n бит памяти, он имеет 2 n состояний! За Например, компьютер с тремя битами памяти может использовать эти биты для представляют восемь состояний:
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
Количество возможных состояний в типичном большом компьютере больше, чем количество атомов в галактике.)
Сейчас я расскажу о теоретической модели машины. с бесконечной памятью. Вы можете задаться вопросом, почему стоит изучать такие машины, так как любая реальная машина должна быть ограничена в памяти. В Ответ связан с моим примером о 20 000 уровней скобок. Теоретически можно написать регулярное выражение для таких струны. Чтобы показать вам, как это делается, вот регулярное выражение до трех уровней:
(Я нарисовал рамки вокруг реальных символов правил алфавита, чтобы чтобы вам было легче различать круглые скобки, которые являются символами во входных строках, и скобки, которые являются частью клей, который скрепляет регулярное выражение.)
Нет теоретической проблемы с расширением этого регулярного выражения. чтобы разрешить до 20 000 скобок. Но машина на основе этой техники будет очень большим и сложным. Вместо этого имеет смысл притвориться , что у компьютера бесконечный объем доступной памяти и используйте формальную систему (например, производственные правила, которые я вкратце упомянул) это зависит от бесконечной памяти. Такая формальная система приводит к более короткое и элегантное выражение правила сбалансированных круглых скобок.На практике мы можем предоставить достаточно памяти для любой из строк нашего программа действительно встретится.
Машины Тьюринга
Один из способов исследования бесконечных машин — это представить, что они представленные диаграммами состояний, как у конечных автоматов, но с бесконечным количеством состояний. Например, вот картинка счетчика круглых скобок бесконечной емкости:
Проблема с этой идеей в том, что трудно точно смоделировать то, что имеется в виду этот ряд точек справа.Мы не можем иметь полное формальное описание бесконечно сложной машины.
Вместо этого подумайте, что вы, , делаете, когда вам нужно решить проблему. слишком сложен, чтобы поместиться в вашей собственной памяти. Вы не строите себе больший мозг; вы получаете карандаш и бумагу. То есть вы используете внешнее хранилище . Вы можете представить, что ваш мозг — это конечное состояние. машина, но у нее есть доступ к бесконечному запасу бумаги.
Конечно, это разделение необходимой информации о проблеме на конечное внутреннее состояние и бесконечная внешняя память также очевидным образом моделирует реальные компьютеры.Внутреннее состояние в модели представляет собой внутреннюю память компьютера, а внешняя память в модели представляет собой такие запоминающие устройства, как диски и ленты. Чтобы решить большую проблему, вам не нужно покупать компьютер побольше; вам просто нужно время от времени переключать дискеты.
Вы могли подумать, что математическая модель, о которой я говорю, была основанный на аналогии с реальными компьютерами, и что мой рассказ о конечных состояниях мозг это просто совпадение. Но на самом деле эта модель была изобретена Алан М.Тьюринг в 1936 году, еще до того, как появились компьютеры! Это было человек Решение проблем, которое Тьюринг хотел смоделировать с помощью машины.
Что такое машина Тьюринга? Начните с представления конечного автомата с разными возможными выходами, как у сумматора, который мы видели ранее. Прикрепил к этой машине идет лента безграничной длины. Символы из некоторых алфавит, как и символы ввода и вывода машины, можно записать на ленте. Есть механизм чтения и записи, как у головок магнитофона, который может перемещаться по ленте.
Так же, как каждое состояние машины может иметь вывод, связанный с это, каждое состояние может также действовать, чтобы повлиять на ленту: она может перемещаться голову на один символ в любом направлении, и это может изменить символ в текущей позиции головы.
Фактически, мы упрощаем формальное описание машины на использование ленты в качестве устройства ввода / вывода, а также устройства хранения. То есть мы можем начать с некоторой последовательности уже написанных символов на ленте. Эта последовательность служит входными данными для машины; государственный переходы основаны на символе под головкой ленты, а не на символе из другого источника.Аналогично, выход из состояния (если есть) написано на ленте.
В чем-то аналогично концепции принимающего состояния, описанной нами ранее. Например, машина Тьюринга может иметь остановок и состояний. Когда машина переходит в состояние остановки, она останавливает свою работу. Есть больше никаких переходов между состояниями. Выход из машины — это то, что последовательность символов, которые он оставляет записанными на ленте.
Тезис Тьюринга
Тьюринг изобрел свою абстрактную машину, потому что пытался формализовать идея эффективной процедуры : что значит указать техника для решения некоторой проблемы достаточно хорошо, чтобы мы могли быть уверены это действительно будет работать? В качестве аналогии подумайте о направлениях движения. отсюда куда-нибудь.Кто-то может передать вам листок бумаги с список инструкций типа «Когда вы доберетесь до АЗС налево, поверните направо «. Но иногда вы получаете указания, были недостаточно осторожны. Возможен резкий поворот направо и небольшой Правый поворот доступен возле АЗС. Там может быть развилка дорога еще до того, как вы доберетесь до заправочной станции.
Идея Тьюринга состоит в том, что любая проблема, для которой существует любой эффективный Процедуру можно смоделировать с помощью машины Тьюринга. Фраза «любой эффективный процедура «включает в себя работу человеческого разума.Если Тьюринг прав, любую проблему, которую может решить человек, можно запрограммировать. для компьютера.
Это утверждение не может быть доказано или опровергнуто математически. потому что не существует предварительного формального определения «эффективной процедуры» с которыми можно сравнить машины Тьюринга. Кроме того, возможно, что представление о процедуре как-то не охватывает все виды думать, что люди делают. Может быть, это правда, например, что компьютеры потенциально так же могущественны, как и люди, в решении проблем, но «решают проблемы «может оказаться неподходящим описанием что происходит, когда мы чувствуем эмоции.Если это повернулось если быть правдой, мы, , должны ожидать, что компьютер станет мировым когда-нибудь чемпионом по шахматам, но мы, , не должны ожидать, что станет поэт-чемпион мира.
Но этот возможный вывод подвергался критике с обеих сторон. Немного люди думают, что эмоции на самом деле — это , которые можно вычислить. процедуры. Программа Кеннета Колби под названием Parry пытается моделировать поведение параноидального человека путем манипулирования переменными для таких эмоций, как гнев и страх.С другой стороны, некоторые люди думаю, что даже шахматы не относятся к сфере того, что люди делают это, выполняя эффективные процедуры в смысле Тьюринга. Эти люди говорят, что шахматный мастер не анализирует шахматную доску. шаг за шагом, как компьютер. Он смотрит на доску как единое целое, а важные функции просто возникают в уме каким-то процессом, который все еще остается довольно загадочным.
известен как , так это то, что несколько других математических моделей эффективных было показано, что процедуры эквивалентны машинам Тьюринга, в в том же смысле, в котором регулярные выражения эквивалентны конечному состоянию машины.Например, все популярные языки программирования Эквивалент Тьюринга. Нет такой вещи, как вычисления, которые могут должно выполняться в Logo, но не в Pascal, или наоборот. (Конечно, один язык может быть более удобным , чем другой для данной проблемы.)
Теорема об остановке
Я не буду вдаваться в конкретные примеры программирования машины Тьюринга здесь. Это заняло бы слишком много места для одной главы; если вы Заинтересованные вы должны продолжить тему в книге по теории автоматов.Но я хочу привести один пример теоретической ценности машин Тьюринга.
У вас, несомненно, был опыт написания программы Logo с ошибкой
что вызывает «бесконечный цикл» — вы запускаете программу, и она просто сидит там
навсегда, когда вместо этого предполагается вычислить и распечатать некоторые результаты.
Это неприятная ошибка, потому что вы никогда не уверены, что
программа действительно не работает или работает очень медленно. Может, если бы ты подождал
через минуту он придет к ответу.Было бы здорово, если бы
когда вы запускали программу, Logo может выводить сообщение об ошибке, например Эта программа имеет бесконечный цикл , как и для других ошибок?
Оказывается, бесконечные циклы, как правило, не могут быть обнаружены автоматически. Конечно, некоторые бесконечные петли очень легко обнаружить, и мы можем писать программы, которые ловят определенные категории бесконечного цикла. Но мы не можем написать программу, которая гарантировала бы, что поймает бесконечное число циклы в программах на языке Logo или любом другом языке, эквивалентном Тьюрингу.В Тот факт, что это невозможно, называется теоремой об остановке.
Сложно понять, что говорит теорема об остановке, потому что он включает машины Тьюринга, которые манипулируют машинами Тьюринга как данными, которые это своего рода ссылка на себя, похожая на рекурсию. Самостоятельная ссылка всегда трудна о чем можно говорить и может привести к парадоксам наподобие классического «Это утверждение ложно «. (Предложение в кавычках истинно или ложно? Если оно истинно, то оно должно быть ложным, потому что так сказано.Но если это ложь, и это говорит это ложь, это действительно должно быть правдой!) Так что давайте действовать осторожно.
Данные, записанные на ленту машины Тьюринга, представляют собой строку символов. Обычно мы выбираем символы для обозначения чего-то значимого; за Например, строка цифр может представлять число. Ранее в этой главе мы использовали строки символов вроде
[1 [[1 A 2] [2 B 3] [3 A 2]] [1 3]]
для представления конечного автомата. Нет причин, по которым мы
не мог поместить , эту строку символов на ленту машины Тьюринга
как его вход.Например, мы могли бы построить машину Тьюринга, которая бы работала
как моя программа fsm , имитирующая конечный автомат, который она нашла
написано на его ленте при запуске.
Разрешение машине Тьюринга моделировать конечный автомат не вызывает вопросы саморекламы. Но машина Тьюринга тоже формальная структура; его тоже можно представить в виде строки символов.
Поскольку представление машины Тьюринга может быть входом для другого
Машина Тьюринга, мы можем разработать машины Тьюринга, которые отвечают на вопросы о
Машины Тьюринга.Например, мы можем написать универсальный Тьюринг
машина, которая имитирует любую машину Тьюринга так же, как fsm любой конечный автомат.
Универсальная машина Тьюринга (симулятор машины Тьюринга) вроде полурешает проблема остановки. Предположим, мы хотим знать, будет ли данная машина остановка после запуска с заданным вводом. (Это все равно, что спросить, не определенная процедура логотипа будет завершена, если она будет вызвана с определенным входных данных.) Мы можем использовать универсальную машину Тьюринга, чтобы смоделировать ту, которую мы увлекающийся.Если машина сделает остановку , мы узнаем об этом. Но если рассматриваемая машина не останавливается , то симулятор тоже не остановится. У нас все еще будет проблема, которая была в первом место — как мы можем быть уверены, что оно не остановится, если мы дадим ему еще один минута?
Чтобы решить проблему остановки, нам нужна машина Тьюринга, которая принимает представление любой машины Тьюринга в качестве входных данных, точно так же, как универсальный Машина Тьюринга. Но этот должен быть гарантированно остановлен, даже если машина ввода не останавливалась.Вот что говорит теорема об остановке: мы не можем делать.
Доказательство теоремы о остановке в логотипе
Что позволяет поставить вопрос о том, может ли машина Тьюринга
решить, остановится ли другая машина Тьюринга для данной входной ленты,
тот факт, что «программа» одной машины Тьюринга может быть представлена как данные
для другой машины Тьюринга. Это также относится к процедурам с логотипом. В
в частности, процедуры более высокого порядка, такие как map и filter манипулировать другими процедурами, принимая их имена в качестве входных данных.Поэтому мы можем использовать Logo
процедуры, иллюстрирующие доказательство теоремы об остановке.
Рассмотрим процедуру Logo с входом, аналогичную процедуре Тьюринга. машина со своей входной лентой. Мы хотим доказать, что логотипа не может быть процедура, которая могла бы сказать, останавливается ли такая процедура для данного ввода. Используемая нами техника называется доказательством от противоречия. В этом Мы предполагаем, что — это такая процедура, а затем покажем, что это предположение приводит к парадоксу.
Итак, давайте представим, что кто-то написал предикат логотипа haltp , который
принимает два входа: имя процедуры и входное значение для этого
процедура. Haltp выведет true , если процедура, которую он тестирует
в конечном итоге остановится при заданном вводе; haltp выходы false , если тестируемая процедура войдет в бесконечный цикл, например
рекурсивная процедура без правила остановки. (На практике, если подумать о
ваш собственный опыт отладки программ, легко определить,
вообще не имеет правила остановки, но не так-то просто убедиться, что остановка
правило всегда в конце концов будет удовлетворено.Подумайте о программе Pig Latin
дано слово из всех согласных в качестве входных. Мы хотим
по пиглатин: слово если сначала memberp: слово [a e i o u] [выходное слово: слово «ay] вывести пиглатинское слово bf: сначала слово: слово конец ? принт халтп "пиглатин" салями истинный ? печать халтп "пиглатин" mxyzptlk ложный
Помните, что haltp сам должен всегда останавливаться , даже
в случае, когда пиглатин не остановится.)
Теперь рассмотрим эту процедуру с логотипом:
попробовать: proc если haltp: proc: proc [цикл] конец зацикливать петля конец
Так как haltp работает, мы предполагаем, на любой логотип процедура с одним входом, она должна работать на , в частности, попробуйте .Что произойдет, если мы скажем
? попробуйте "попробуйте "
Это останавливается или зацикливается? Предположим, это прекратится. try начинает свое
работать, оценивая выражение
haltp "попробовать" попробовать
Поскольку мы сказали, что попытка остановится, если попробуйте в качестве входных данных, haltp выведет true . Из определения следует
попробуйте , этот try вызовет цикл и остановит , а не .Точно так же, если мы начнем с предположения, что try будет зацикливаться, тогда haltp должен выводить false и, следовательно, из определения попробуйте , вы увидите, что попробуйте остановится. Какое бы значение ни было выходы haltp оказываются некорректными.
Это было предположение, что мы можем написать безошибочную haltp , что привело
мы попали в это противоречие, так что это предположение должно быть неверным. Мы не можем писать
процедура Logo, которая автоматически обнаруживает бесконечные циклы в нашем
программы.Подобное доказательство может быть сделано на любом языке, на котором одна программа
может манипулировать другой программой как данными — то есть в любом эквиваленте Тьюринга
язык.
Листинг программы
;;; Интерпретатор конечных автоматов (FSM)
в игру: который
fsm thing word "mach: который
конец
в fsm: machine
открытый текст
setcursor [0 3]
localmake "start startpart: машина
localmake "перемещает movepart: machine
localmake "accept acceptpart: machine
fsm1: start
конец
to fsm1: здесь
ifelse memberp: здесь: принять [принять] [отклонить]
fsm1 (fsmnext: здесь readchar)
конец
в fsmnext: здесь: ввод
пустой
если memberp: input (список char 13 char 10) ~
[print ifelse memberp: here: accept ["| ПРИНЯТЬ |] [" | ОТКАЗАТЬ |]
вывод: начало]
тип: ввод
catch "ошибка [вывод последней находки [fsmtest: здесь: ввод?]: перемещается]
выход -1
конец
в fsmtest: здесь: input: move
output and (equalp: здесь arrowtail: move) ~
(memberp: ввод со стрелкой, текст: перемещение)
конец
;; Отображение состояния машины
принять
дисплей "принять
конец
отказаться
отображать "отклонить
конец
заглушить
дисплей "|
конец
для отображения: текст
localmake "oldpos курсор
setcursor [15 1]
тип: текст
setcursor: oldpos
конец
;; Абстракция данных для машин
в началочасть: машина
сначала вывод: машина
конец
to movepart: machine
вывод первый бф: машина
конец
принять часть: машина
вывод последний: машина
конец
сделать.машина: начало: движется: принять
вывод (список: начало: ходы: принять)
конец
;; Абстракция данных для стрелок
в arrowtail: arrow
вывод сначала: стрелка
конец
в arrowtext: arrow
сначала вывод, но сначала: стрелка
конец
к стрелке: стрелка
последний вывод: стрелка
конец
сделать.arrow: tail: text: head
вывод (список: хвост: текст: голова)
конец
;; Описание машин для игры в угадайку
make "mach2 [1 [[1 AB 1]] [1]]"
make "mach3 [1 [[1 ABC 2] [2 ABC 1]] [1]]"
make "mach4 [1 [[1 A 2] [2 B 3] [3 ABC 3]] [3]]"
make "mach5 [1 [[1 A 2] [1 B 3] [1 C 4] [2 A 1] [3 B 1] [4 C 1]] [1]]"
make "mach5 [1 [[1 ABC 2] [2 B 1]] [1]]"
make "mach6 [1 [[1 A 2] [2 AB 2] [2 C 3] [3 AB 2] [3 C 3]] [3]]"
make "mach7 [1 [[1 AB 1] [1 C 2] [2 C 1]] [1]]"
make "mach8 [1 [[1 A 2] [1 BC 1] [2 A 1] [2 BC 2]] [1]]"
make "mach9 [1 [[1 AB 1] [1 C 2] [2 A 3] [2 B 1] [3 A 1]] [1]]"
make "mach20 [1 [[1 A 2] [1 BC 1] [2 A 2] [2 B 3] [2 C 1]]"
[3 A 2] [3 B 1] [3 C 4] [4 A 2] [4 B 5] [4 C 1]
[5 A 6] [5 BC 1] [6 ABC 6]]
[6]]
;;; Преобразование регулярных выражений в автоматические автоматы (МАШИНА)
на машину: regexp
localmake "nextstate 0"
output optimize определить nondet: regexp
конец
;; Первый шаг: создать возможно недетерминированную машину
в nondet: regexp
если и (wordp: regexp) (equalp count: regexp 1) ~
[выходной ndletter: regexp]
если wordp: regexp [вывод ndor сокращение "предложение: regexp]
если сначала равно: regexp "или [output ndor butfirst: regexp]
если равняется сначала: regexp "* [вывод ndmany last: regexp]
вывод ndconcat: regexp
конец
;; Правило алфавита
на ndletter: письмо
localmake "от NewState
localmake "в NewState
вывод (make.машина: от
(список (make.arrow: from: letter: to))
(список: в))
конец
;; Правило конкатенации
кому: ndconcat: exprs
вывод reduce "строка (карта" nondet: exprs)
конец
в строку: machine1: machine2
вывод (make.machine (startpart: machine1)
(предложение (movepart: machine1)
(splice acceptpart: machine1: machine2)
(movepart: machine2))
(строка (acceptpart: machine1)
(начальная часть: машина2)
(acceptpart: machine2)))
конец
в строкуa: accept1: start2: accept2
если memberp: start2: accept2 [выходное предложение: accept1: accept2]
вывод: accept2
конец
;; Правило альтернатив
к ndor: exprs
localmake "newstart newstate"
localmake "машины (карта" nondet: exprs)
localmake "принимает карту.se "acceptpart: машины
вывод (make.machine: newstart
(предложение map.se "movepart: machines
map.se "or.splice: машины)
ifelse not emptyp find [memberp (startpart?)
(acceptpart?)]
: машины
[fput: newstart: принимает]
[: принимает])
конец
к or.splice: машина
карта вывода [newtail? : newstart] (стрелки.from.start: машина)
конец
;; Правило повторения
кому: ndmany: regexp
localmake "машина nondet: regexp
вывод (make.machine (startpart: machine)
предложение (movepart: machine)
(splice (acceptpart: machine): машина)
fput (startpart: машина) (acceptpart: машина))
конец
;; Генерировать ходы из набора заданных состояний (: принимает), дублируя
;; переходит из начального состояния некоторой машины (: machine).
;; Используется для правила конкатенации для соединения двух ранее разделенных машин;
;; используется для правила повторения, чтобы «соединить» машину с собой.соединять: принимает: машина
вывод map.se [copy.to.accepts?] (arrows.from.start: machine)
конец
до arrows.from.start: machine
выходной фильтр [equalp startpart: machine arrowtail?] movepart: machine
конец
to copy.to.accepts: move
карта вывода [newtail: move?]: принимает
конец
в newtail: arrow: tail
вывод make.arrow: tail (arrowtext: arrow) (arrowhead: стрелка)
конец
;; Сделайте новый государственный номер
Newstate
сделать "nextstate: nextstate + 1"
вывод: nextstate
конец
;; Второй шаг: превратить недетерминированный автомат в детерминированный
;; Также исключает «сиротские» (недоступные) состояния.определить: машина
localmake "перемещает movepart: machine
localmake "принимает acceptpart: machine
localmake "состояния []
localmake "join.state.list []
localmake "newmoves nd.traverse (начальная часть: машина)
вывод make.machine (startpart: machine) ~
: newmoves ~
фильтр [memberp? : состояния]: принимает
конец
к nd.traverse: состояние
если memberp: state: состояния [output []]
make "состояния fput: state: состояния
localmake "newmoves (check.nd filter [equalp arrowtail?: state]: move)
Выходное предложение: newmoves map.se "nd.traverse (карта" стрелка: newmoves)
конец
to check.nd: movelist
если emptyp: movelist [вывод []]
localmake "буква arrowtext first: movelist
localmake "карта сортировки голов" стрелка ~
filter [equalp: letter arrowtext?]: movelist
если пустоp, но сначала: головы ~
[сначала вывод fput: movelist
check.nd фильтр [not equalp: letter arrowtext?]
: movelist]
localmake "участник check.heads: Heads: join.state.list
если не пустоp: check.heads ~
[вывод fput make.стрелка: состояние: сначала буква, но сначала: check.heads ~
check.nd фильтр [not equalp: letter arrowtext?]
: movelist]
localmake "join.state newstate
сделать "join.state.list fput: Heads fput: join.state: join.state.list
сделать "ходы предложения: ходы ~
карта [make.arrow: join.state
arrowtext?
стрелка?] ~
фильтр [memberp arrowtail? : Heads]: движется
если не emptyp, найдите [memberp? : принимает]: головы ~
[make »принимает предложение: принимает: присоединяется.государственный]
вывод fput make.arrow: state: letter: join.state ~
check.nd фильтр [not equalp: letter arrowtext?]: movelist
конец
сортировать: список
если пустоp: список [вывод []]
вывод вставить сначала: сортировка списка, но сначала: список
конец
для вставки: значение: отсортировано
если пустоp: отсортировано [вывод (список: значение)]
если: значение = первое: отсортировано [вывод: отсортировано]
if: value Объединить избыточные состояния.
;; Также комбинирует стрелы с одинаковой головой и хвостом:
;; [1 A 2] [1 B 2] -> [1 AB 2].
оптимизировать: машина
localmake "массив stubarray: nextstate
foreach (movepart: machine) "массив.спасти
localmake "указывает sort fput (startpart: machine) ~
карта "стрелка movepart: машина
localmake "start startpart: машина
foreach reverse: состояния [optimize.state? ?отдых]
вывод (make.machine: start
map.se [fix.arrows? элемент ? : stubarray]: состояния
фильтр [memberp? : состояния] acceptpart: machine)
конец
в array.save: move
setitem (стрелка: перемещение): stubarray ~
stub.add (arrow.stub: move) (элемент (arrowtail: move): stubarray)
конец
заглушить.добавить: заглушка: список заглушек
если пустойp: список-заглушка [вывод (список: заглушка)]
if (stub.head: stub) (назад к содержанию)
НАЗАД
резьба главы СЛЕДУЮЩАЯ
Брайан Харви,
[email protected]
Анализ характеристик смешанного транспортного потока обычных и автономных транспортных средств с использованием сотовых автоматов
Ожидается, что технология автономных транспортных средств произведет революцию в работе систем автомобильного транспорта.Уровень проникновения автономных транспортных средств будет низким на ранней стадии их развертывания. Это сложная задача — изучить влияние автономных транспортных средств и их проникновение на динамику неоднородного транспортного потока. Настоящая статья направлена на исследование этого вопроса. Усовершенствованный клеточный автомат был использован в качестве платформы моделирования для нашего исследования. В частности, два набора правил смены полосы движения были разработаны для решения проблемы мягкого и агрессивного поведения при смене полосы движения. Благодаря обширным исследованиям моделирования мы получили несколько многообещающих результатов.Во-первых, внедрение автономных транспортных средств в дорожное движение могло бы значительно улучшить транспортный поток, особенно пропускную способность дороги и скорость свободного движения. И уровень улучшения увеличивается с увеличением скорости проникновения. Во-вторых, частота смены полосы движения между соседними полосами движения изменяется вместе с плотностью движения по кривой, похожей на фундаментальную диаграмму. В-третьих, влияние автономных транспортных средств на характеристики коллективного транспортного потока в основном связано с их умными маневрами при смене полосы движения и следовании за автомобилем, и кажется, что влияние следования за автомобилем более выражено.
1. Введение
В течение последнего десятилетия предпринимались интенсивные усилия по разработке различных систем автоматизации транспортных средств. Помимо своих замечательных способностей в выполнении различных задач вождения, автоматизированные / автономные транспортные средства могут иметь потенциал влиять на работу транспортных систем с точки зрения эффективности, безопасности и экологичности [1–5]. В частности, автономные транспортные средства (AV) имеют незначительную задержку времени реакции по сравнению с обычными транспортными средствами (RV) и могут двигаться с гораздо меньшим интервалом или шагом, возможно, с широким спектром скоростей.Поэтому ожидается, что пропускная способность дорог с АВТ будет увеличена [6–9]. AV также могут получать доступ к текущему состоянию соседних транспортных средств, чтобы принимать более информированные и разумные решения при маневрах по смене полосы движения. Это также может положительно сказаться на пропускной способности дорог. Кроме того, AV могут помочь снизить расход топлива и выбросы [10]. Тем не менее, современные технологии автоматизации транспортных средств обычно разрабатываются в интересах отдельных транспортных средств, без четкого представления о возможных преимуществах и недостатках, которые они могут внести в характеристики транспортного потока.
Уровень проникновения автономных транспортных средств будет низким на ранней стадии их развертывания, и ожидается, что жилые дома и автофургоны будут вместе путешествовать по дорогам в течение длительного периода времени. Сочетание AV и RV может показать некоторые сложные характеристики транспортного потока, в отличие от только RV [11, 12]. До сих пор исследования такого смешанного транспортного потока все еще весьма ограничены [13, 14]. Необходимы соответствующие модели и подходы к моделированию на всех уровнях (микроскопическом, мезоскопическом и макроскопическом), которые могли бы позволить должным образом отразить развивающуюся динамику и возможности смешанного транспортного потока.
Этот документ предназначен для изучения характеристик смешанного транспортного потока RV и AV, включая пропускную способность, фундаментальную диаграмму и частоту смены полосы движения. Поскольку AV-системы еще не поступили на рынок, текущие исследования в отношении AV-систем проводятся либо с помощью полевых экспериментов, которые в основном решают проблемы на уровне отдельного транспортного средства, либо с помощью имитационных исследований, которые также могут иметь последствия на уровне транспортного потока. Доступных имитационных исследований пока недостаточно. И () эффекты АВ не были ни полностью проанализированы, ни всесторонне интерпретированы; () выявленные эффекты не всегда согласовывались; () нет единого подхода к моделированию.Эта статья следует моделированию. Поскольку нас больше всего беспокоит поведение отдельных транспортных средств в общей динамике транспортного потока, мы бы выбрали для этой работы либо мезоскопические имитационные модели, такие как клеточные автоматы (CA), либо микроскопические имитационные модели, такие как VISSIM и AIMSUN. Как обсуждается в литературе, важным вопросом является баланс между производительностью модели и ее сложностью. Учитывая способность CA моделировать сложную нелинейную динамику потока трафика, несмотря на его существенную простоту, мы решили использовать CA для этого исследования.В частности, в этой работе используется улучшенная модель клеточного автомата (КА). Краткий обзор литературы по СА представлен ниже.
Первой моделью клеточного автомата, которая была представлена для моделирования дорожного движения, является модель NaSch, предложенная Нагелем и Шрекенбергом [15]. СА — это, по сути, дискретная пространственно-временная динамическая система, основанная на локальных правилах [16]. Используя CA, сложность и возникновение транспортных систем можно смоделировать и смоделировать с помощью кратких условий и правил [17]. Благодаря своей простоте, эффективности и действенности, большое количество расширенных моделей CA было разработано после модели NaSch [18].Например, Чоудхури и др. [19] разработали модель симметричных двухполосных клеточных автоматов (STCA), которая позже была расширена Педерсоном и Рухоффом [20] на многополосный случай. Модели CA также использовались для имитации гетерогенного транспортного потока [21–24].
Эта работа моделирует и моделирует поток гетерогенного трафика RV и AV с использованием улучшенной модели STCA в попытке определить влияние AV на динамику смешанного потока трафика. Считается, что разные уровни проникновения AV отражают постепенный рост AV в потоке трафика.В основе нашей модели мезоскопического трафика на основе CA лежат два конкретных набора правил смены полосы движения для AV и RV. Одна из основных целей этого исследования — определить влияние AV на частоту смены полосы движения всех задействованных транспортных средств. По этой причине ниже представлен краткий обзор литературы по изучению смены полосы движения.
Частая смена полосы движения определенно влияет на транспортный поток [25], а неправильная смена полосы движения считается основным источником заторов и аварий [26, 27].Гиппс представил, вероятно, первую хорошо известную модель смены полосы движения для городского движения [28], в то время как несколько других моделей были разработаны на основе модели Гиппса и распространены на случай автострад [15, 29]. Ахмед и др. [30] применили теорию случайной полезности для моделирования поведения при смене полосы движения и определили процесс принятия решения об изменении полосы движения. Толедо [31] разработал схему дискретного выбора для моделирования интегрированных смен полос движения и оценил соответствующие параметры. В условиях плотного или перегруженного движения транспортному средству, пытающемуся сменить полосу движения, требуется взаимодействие по крайней мере с одним следующим транспортным средством на целевой полосе.Хидас [25] разработал модель совместной смены полосы движения, основанную на концепции «любезности водителя». Транспортное средство, которое хочет сменить полосу движения, отправляет запрос вежливости последующим транспортным средствам на целевых полосах движения; запрос оценивается каждым последующим автомобилем. Если транспортное средство проявляет любезность к запрашивающему транспортному средству, оно снижает его ускорение, чтобы обеспечить свободный зазор достаточной длины.
Всесторонне проанализировав предыдущие работы по смене полос движения, Kesting et al. [32] предложили модель MOBIL (Минимизация общего торможения, вызванного сменой полосы движения) для решения проблемы совместной смены полосы движения интеллектуальных транспортных средств.MOBIL эмулирует решение о смене полосы движения как компромисс между стимулом, который транспортное средство намеревается осуществить смену полосы движения, чтобы набрать более высокую скорость, и вежливостью, которую это транспортное средство проявляет, чтобы как можно меньше беспокоить соседние транспортные средства. в целевой полосе. На основе MOBIL другие исследователи продолжили изучение интеллектуальных моделей смены полосы движения [33]. С эмпирической точки зрения, исследования поведения при смене полосы движения были гораздо менее полными, чем исследования поведения при продольном вождении (например, следование за автомобилем) из-за отсутствия обширных данных о траектории транспортного средства [34].Появление технологий автономных и подключенных транспортных средств открывает большие возможности в будущем.
Работа организована следующим образом. В разделе 2 представлена структура моделирования и симуляции, основанная на улучшенных клеточных автоматах, и, в частности, представлены два конкретных набора правил для смены полосы движения. В разделе 3 проводятся обширные имитационные исследования с представлением многообещающих результатов. Раздел 4 завершает статью.
2. Моделирование
2.1. Настройка моделирования
Типичная модель CA трафика учитывает три ключевых компонента: дорожную среду, состояния ячеек и местные правила перехода.Мы рассматриваем трехполосный участок автострады, который представлен решеткой из числа ячеек на полосу. Длина камеры составляет 5 метров, что примерно соответствует средней длине транспортного средства. Временной шаг симуляции установлен равным 1 секунде, а временной горизонт симуляции составляет 10 000 временных шагов. Скорость любого обычного транспортного средства находится на одном из шести дискретных уровней, которые составляют 0–5 ячеек за временной шаг. «0» означает, что транспортное средство стоит на месте, а «5» означает, что транспортное средство может проехать через 5 ячеек за один временной шаг, а соответствующая скорость составляет 90 км / ч.С другой стороны, максимальная скорость любого автономного транспортного средства составляет 7 ячеек за временной шаг (т. Е. 126 км / ч). Ячейка в любой момент времени находится в одном из двух состояний: свободна или занята транспортным средством. Принимая во внимание информацию о скорости транспортного средства, мы можем рассматривать состояние каждой ячейки как изменяющееся от -1 до 7, где «-1» относится к свободному состоянию, а «0–7» — к статусу занятости с соответствующей скоростью транспортного средства на уровне 0–7.
2.2. Основные правила обновления состояния системы
Некоторые правила основаны на обновлении состояний всех транспортных средств за один временной шаг от до.Каждое правило касается определенного маневра транспортных средств. В последовательности обновления системы на каждом временном шаге эти правила представлены следующим образом: (i) смена полосы движения, (ii) ускорение:, (iii) детерминированное замедление:, (iv) рандомизация:, (v) положение обновления:, где обозначает скорость определенного транспортного средства в момент времени, обозначает максимальный предел скорости, который равен 5 или 7 в этой работе, представляет собой расстояние между транспортными средствами на той же полосе движения и обозначает текущее положение автомобиля.
Для каждого временного шага эти правила последовательно рассматриваются для каждого транспортного средства, чтобы обновить свое состояние, и маневр с изменением полосы движения всегда выполняется первым, правила которого подробно описаны в разделе 2.3. Правило ускорения гласит, что любое транспортное средство не может увеличивать свою скорость за один временной шаг более чем на один уровень. Правило замедления означает, что транспортное средство сохраняет свою текущую скорость, если только ему не нужно замедляться, чтобы адаптироваться к текущему расстоянию между передними колесами. Правило рандомизации применяется только к RV с вероятностью.Это означает, что часть водителей не может постоянно поддерживать текущую скорость и может случайным образом замедлять свои автомобили. Правило обновления местоположения гласит, что транспортные средства обновляют свое местоположение в соответствии со своей текущей скоростью. Это правило взято из однополосной модели NaSch.
2.3. Правила смены полосы движения
Предполагается, что любое транспортное средство, будь то AV или RV, подчиняется основному правилу, согласно которому смена полосы движения может производиться только с наименьшими затратами на снижение скорости соседних транспортных средств; то есть транспортное средство сменило бы полосу движения только в том случае, если бы соседним транспортным средствам на целевой полосе не пришлось бы соответственно слишком сильно замедляться.Кроме того, предполагается, что смена левой полосы движения имеет первый приоритет, если смена полосы движения в любом направлении приемлема.
Основное различие между RV и AV с точки зрения смены полосы движения состоит в том, что AV может связываться с соседними AV в целевых полосах движения для возможности более гибкой смены полосы движения. В частности, рассматриваются два набора правил смены полосы движения, а именно правила вежливой смены полосы движения (PLC) и правила агрессивной смены полосы движения (ALC). В зависимости от ситуации AV может следовать либо PLC, либо ALC, в то время как RV может следовать только правилу ALC.
(1) Вежливая смена полосы движения (ПЛК). Фундаментальная гипотеза, касающаяся ПЛК, состоит в том, что водители осторожны, когда пытаются сменить полосу движения; то есть их маневры по смене полосы движения не должны мешать движению соседних транспортных средств по соседним полосам движения. Это в основном согласуется с моделью MOBIL с ее параметром вежливости, равным 1. Вместо того, чтобы предполагать эгоцентричное поведение в большинстве моделей смены полосы движения, правила PLC поддерживают более альтруистическое поведение.
Вообще говоря, при изучении смены полосы движения необходимо учитывать два аспекта: стимулы и безопасность. Только при соблюдении некоторых критериев, касающихся обоих аспектов, автомобили меняют полосу движения. Мы ссылаемся на модель STCA [19], чтобы установить критерии стимулирования и безопасности для PLC. Правила PLC проиллюстрированы на рисунке 1, где транспортные средства, выделенные красным цветом, представляют собой AV, готовящиеся к смене полосы движения.
Как показано на рисунке 1 (a), транспортное средство выбирает левую полосу движения в качестве целевой полосы и может выполнять смену полосы движения, если выполняются следующие условия: где обозначает скорость th транспортного средства в момент времени , обозначает максимальную скорость предел th транспортного средства, и,, и представляют собой расстояние впереди транспортного средства на той же полосе движения, расстояние впереди транспортного средства на левой полосе и расстояние сзади транспортного средства на левой полосе.Аналогичная номенклатура применяется к случаю смены правой полосы движения.
Уравнение (1) формулирует критерий стимулирования, в то время как (2) и (3) обращаются к критерию безопасности. Точнее, (1) означает, что текущее расстояние между фронтами недостаточно, если текущая скорость увеличивается на один уровень; (2) и (3) означают, что левое (целевое) переднее расстояние достаточно для смены полосы движения, а левое заднее расстояние абсолютно безопасно. Если (1) — (3) не соблюдены, автомобиль проверяет возможность смены полосы движения с правой стороны:
Если (1), (4) и (5) не выполняются, автомобиль остается на текущей полосе.Когда выполняются (1) — (3) или (1), (4) и (5), транспортное средство может сменить полосу движения с вероятностью. Этот параметр введен, чтобы отразить индивидуальность транспортных средств при смене полосы движения (т.е. даже при тех же условиях, которые благоприятствуют смене полосы движения, некоторые транспортные средства могут не делать этого).
Как показано на рисунках 1 (b) и 1 (c), рассматриваются еще два набора правил для решения проблемы совместной смены полосы движения двух AV: где обозначает длину транспортного средства. Уравнения (6) и (7) соответствуют рисунку 1 (b), где два AV взаимодействуют посредством взаимодействия, чтобы выполнять смену полосы движения в противоположных направлениях.Уравнения (8) и (9) относятся к случаю, показанному на Рисунке 1 (c), где два AV взаимодействуют для смены полосы движения в одном направлении. Применяется параметр вероятности.
Предполагается, что в этой работе правила PLC соблюдаются только AV, в то время как правила ALC, которые будут представлены ниже, могут соблюдаться как AV, так и RV.
(2) Агрессивная смена полосы движения (ALC). ALC представляет собой набор более реалистичных правил смены полосы движения, чем PLC, особенно для RV. Исследования поведения внедорожников при смене полосы движения [35, 36] показывают, что более медленные движущиеся впереди машины во многих ситуациях побуждают следующих водителей задуматься об обгоне.Кроме того, 95% водителей предпочли бы менять полосу движения только в том случае, если расстояние сзади на целевой полосе превышает длину 3-х секций (15 метров), а их скорость выше, чем у следующих транспортных средств на целевой полосе [37, 38]. Вдохновленные этими выводами, мы разработали правила ALC, чтобы дополнить правила PLC: если транспортное средство является RV, устанавливается равной длине 3 ячеек; в противном случае устанавливается равным длине 2 ячеек для представления различной точности поведения AV и RV.
(3) ПЛК или ALC для AV. При наличии AV в определенный момент времени, если выполняются условия для его выполнения PLC, он выбирает PLC; в противном случае, если условия для ALC выполнены, он выбирает ALC с агрессией с определенной вероятностью, что указывает на то, что этот маневр повлияет на скорости соседних транспортных средств. Однако, если ни один из маневров по смене полосы движения невозможен, он остается в текущей полосе движения (см. Также рисунок 3).
3. Численное моделирование и анализ результатов
3.1. Схема моделирования
Как показано на Рисунке 1, при исследовании моделирования рассматривался участок автострады с 3 полосами движения без съездов и съездов.Участок состоит из 50 ячеек (т.е. длина участка 250 м). Максимальная скорость обычного или автономного транспортного средства составляет 5 или 7 ячеек за временной шаг. Пусть , и обозначают общее количество транспортных средств, AV и RV на моделируемом участке. Периодическое граничное условие рассматривается как обычная практика при моделировании на основе клеточных автоматов. В начале каждой симуляции только некоторые ячейки заняты транспортными средствами, и эти начальные местоположения выбираются случайным образом.
Обозначьте , , , и средний поток, среднюю скорость, среднюю плотность участка и плотность полосы движения ().Более конкретно, и поток может быть определен как
Моделирование запускалось 20 раз для каждого сценария. Временной горизонт моделирования составляет 20000 временных шагов, и для каждого запуска моделирования результат первых 10 4 временных шагов моделирования отбрасывался, чтобы удалить переходные эффекты, а результаты следующих 10 4 временных шагов были записаны. .
3.2. Влияние AV на характеристики потока трафика
На рисунке 2 показаны характеристики смешанного потока трафика, где легенда касается различных пропорций AV (т.е.e., уровень проникновения AV на рынок), а сплошная / пунктирная линия для каждой пропорции AV относится к правилам PLC / ALC. Во-первых, на рис. 2 (а) представлена зависимость скорости от плотности, полученная с помощью данных моделирования. С увеличением доли AV кривая скорость-плотность сдвигается вправо. Это указывает на то, что, во-первых, увеличение соотношения AV увеличивает среднюю скорость при той же плотности, а во-вторых, при использовании большего количества AV весь поток трафика может выдержать более высокую плотность для любой заданной скорости.Все это в основном согласуется с нашим общим пониманием возможностей AV, особенно с их незначительной задержкой времени реакции. Во-вторых, на рис. 2 (b) представлено соотношение плотности потока, извлеченное из данных моделирования. Очевидно, что включение AV значительно увеличивает проходимость дороги и скорость свободного движения. В частности, пропускная способность составляет около 2000 автомобилей в час при нулевом процентном соотношении AV () и становится 3070 автомобилей в час, когда все автомобили являются AV (). Скорость свободного хода составляет около 78,85 км / ч, когда она становится равной 115.При 20 км / ч примерно на 46% выше. Кроме того, увеличение доли AV также немного улучшает критическую плотность, указывая на то, что введение AV делает весь поток трафика более стабильным. С другой стороны, использование разных правил смены полосы движения (PLC или ALC), похоже, не имело большого значения. Для более конкретного вывода по этому вопросу необходимы дальнейшие исследования.
3.3. Влияние вероятности смены полосы движения
Как уже упоминалось, при соблюдении некоторых предустановленных условий транспортные средства могут менять полосу движения или нет, и в наших исследованиях моделирования вероятность назначается так, что только часть транспортных средств-кандидатов решает сменить полосу движения.На рисунке 4 показано влияние на фундаментальную диаграмму при различных пропорциях AV, где учитывается только правило смены полосы движения ALC. Ясно, что существует контраст между рисунками 2 и 4: участие AV действительно значительно улучшает характеристики потока трафика (рисунок 2), в то время как влияние смены полосы движения на поток кажется намного меньше, чем ожидалось. Это может указывать на то, что изменение маневров AV при следовании за автомобилем (по сравнению с RV) вносит больший вклад в улучшение характеристик транспортного потока, чем более разумная операция AV с изменением полосы движения.Чтобы подробнее изучить влияние смены полосы движения, мы рассмотрим частоту смены полосы движения.
3.4. Частота смены полосы движения
В этом разделе мы сосредоточимся на случае смены полосы движения и исследуем ее детали. Прежде всего, частота смены полосы движения между полосами движения определяется следующим образом: где числитель относится к общему количеству случаев смены полосы движения между полосой движения и полосой движения за горизонт моделирования, а знаменатель представляет общее количество транспортных средств, участвующих в всю симуляцию.
Результаты моделирования представлены на рисунке 5, где размер (высота) каждой части рисунка относится к (%), а размеры и относятся к плотности движения полос и. На рисунках 5 (a) и 5 (c) рассматривается случай, когда и, а на рисунках 5 (b) и 5 (d) рассматривается случай, когда и. Кроме того, рисунки 5 (a) и 5 (b) относятся к правилу PLC, а рисунки 5 (c) и 5 (d) — к правилу ALC. Для простоты значения плотности взяты по пунктирной диагональной линии на нижней плоскости на каждом подфигуре.
Обращаясь к рисунку 5 (a), мы видим, что с каждым коэффициентом AV альфа, эволюционирует по кривой, подобной фундаментальной диаграмме, по плотности полос и, и это фактически согласуется с нашим интуитивным пониманием; то есть, когда плотность обеих полос низка, транспортные средства имеют больше свободы при смене полосы движения и увеличивается с количеством транспортных средств на дорогах до достижения критической / поворотной точки, а затем начинает уменьшаться. Кроме того, чем больше задействовано AV, тем меньше ценность.Это связано с тем, что AV могут управлять процессом следования за автомобилем более эффективно даже с гораздо меньшим интервалом между автомобилями, чем RV, и, следовательно, имеют меньше стимулов к смене полосы движения. А в крайнем случае, когда все автомобили являются AV, нет необходимости вообще менять полосу движения, как показано черной кривой на рисунке 5 (a). Сравнение рисунков 5 (a) и 5 (c) с рисунками 5 (b) и 5 (d) показывает, что использование ALC вместо PLC может существенно увеличиться, хотя влияние на общие характеристики потока трафика не так очевидно (см. и пунктирные линии на рисунке 2).
Интересно отметить, что поворотные точки на Рисунке 5 в большинстве случаев довольно близки к тем, которые показаны на Рисунке 2, с точки зрения плотности движения (около 40 автомобилей / км) (подробности см. В Таблице 1). Это указывает на то, что при низкой плотности основного трафика приветствуется больше изменений полос движения, а также это полезно для лучшего использования пропускной способности дороги. А около критической точки как стимул, так и возможность смены полосы движения максимизируются, в то время как поток также достигает своего пика. После этого смена полосы движения становится все менее практичной.Результаты моделирования также показывают, что критические / поворотные точки не очень чувствительны к значениям отношения AV.
| |||||||||||||||||||||||||||||||||||||||||||||||||
3.5. Степень затора
Когда скорость транспортного средства составляет 0 или 1 ячейку за временной шаг, мы говорим, что транспортное средство испытывает затор, и, таким образом, степень затора (CD) рассчитывается следующим образом: где обозначает количество загруженных транспортных средств на всем горизонте моделирования T и обозначает общее количество транспортных средств, задействованных на всем горизонте моделирования.Естественно, что CD увеличивается с плотностью (см. Рисунок 6). Присутствие АВ снижает КД при тех же условиях плотности. В частности, до того, как плотность достигнет критической плотности 40 автомобилей / км, что соответствует потоку пропускной способности, участие AV определенно помогает удерживать CD на более низком уровне. По всему спектру плотности кажется, что смешанный поток трафика с долей AV, равной 50%, лучше всего работает для поддержания постоянно более низкого CD. Авторы продолжают работать над изучением механизма, лежащего в основе этого наблюдения.
4. Выводы
В данной статье изучалось влияние автономных транспортных средств на характеристики смешанного транспортного потока. Поскольку на дорогах действительно нет автономных транспортных средств, текущие исследования в основном проводятся с помощью моделирования. На основе улучшенной модели клеточного автомата для этой работы была разработана платформа моделирования.
Следующие выводы были получены путем интенсивных исследований с помощью моделирования: (1) Пропускная способность и скорость свободного потока положительно увеличиваются с увеличением скорости проникновения автономных транспортных средств.(2) Частота смены полосы движения между соседними полосами движения изменяется вместе с плотностью движения вдоль кривой, подобной фундаментальной диаграмме. (3) Влияние интеллектуальной смены полосы движения автономными транспортными средствами на общие характеристики транспортного потока кажется гораздо менее выраженным, чем это умных автомобилей следующих.
Дальнейшая работа проводится для решения расширенных и более практичных сценариев движения.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Вклад авторов
Янцзэси Лю и Цзинцю Го внесли равный вклад в это исследование.
Выражение признательности
Эта работа была частично поддержана Китайской программой Чжэцзян Цяньрен на 2013–2018 гг., Шанхайской программой Пуцзян и Национальным фондом естественных наук Китая в рамках грантов 51478428 и 71671126.
Изучение машин Мура на основе входных-выходных трасс
Митчелл, TM: Машинное обучение. Макгроу-Хилл, Нью-Йорк (1997)
Google ученый
Вандрагер, Ф .: Модельное обучение. Commun. ACM 60 (2), 86–95 (2017)
Статья Google ученый
Трипакис, С .: Дизайн на основе данных и на основе моделей. В: 1-я Международная конференция IEEE по промышленным киберфизическим системам (ICPS) (2018)
Ljung, L .: System Identification: Theory for the User, 2nd edn. Прентис-Холл, Верхняя Седл-Ривер (1999)
Google ученый
Солар-Лезама, А .: Программный скетч. СТТТ 15 (5–6), 475–495 (2013)
Статья Google ученый
Гулвани, С .: Автоматизация обработки строк в электронных таблицах с использованием примеров ввода-вывода. In: 38th POPL, pp. 317–330 (2011)
Seshia, S.A .: Sciduction: объединение индукции, дедукции и структуры для проверки и синтеза. В: DAC, стр. 356–365 (2012)
Ray, B., Поснетт, Д., Фильков, В., Деванбу, П .: Масштабное исследование языков программирования и качества кода на github. В: ACM SIGSOFT, FSE’14 (2014)
Алур, Р., Мартин, М., Рагхотаман, М., Стерджиу, К., Трипакис, С., Удупа, А. государственные протоколы из сценариев и требований. В: HVC, том 8855 LNCS. Springer (2014)
Алур, Р., Трипакис, С .: Автоматический синтез распределенных протоколов. Новости SIGACT 48 (1), 55–90 (2017)
MathSciNet Статья Google ученый
Зеллер, А .: Почему программы терпят неудачу — Руководство по систематической отладке, 2-е изд. Академик Пресс, Кембридж (2009)
Google ученый
Кохави, З .: Теория переключений и конечных автоматов, 2-е изд. Макгроу-Хилл, Нью-Йорк (1978)
Google ученый
де ла Игера, С .: Грамматический вывод: обучающие автоматы и грамматики. КУБОК, Кембридж (2010)
Google ученый
Gold, E.M .: Определение языка в пределе. Инф. Контроль 10 (5), 447–474 (1967)
MathSciNet Статья Google ученый
Раффельт, Х., Штеффен, Б .: Learnlib: библиотека для обучения автоматов и экспериментов, т. 3922, pp. 377–380 (2006)
Verwer, S., Hammerschmidt, C.: flexfringe: пакет для обучения пассивных автоматов, стр. 638–642 (2017)
Ончина, Дж., Гарсия, П., Видаль, Э .: Изучение дополнительных преобразователей для задач интерпретации распознавания образов. IEEE Trans. Pattern Anal. Мах. Intell. 15 (5), 448–458 (1993)
Артикул Google ученый
Гиантамидис, Г., Трипакис, С .: Изучение машин Мура по трассировкам ввода-вывода. В: Фитцджеральд, Дж. С., Хайтмейер, С. Л., Гнеси, С., Филиппу, А. (ред.) 21-й Международный симпозиум по формальным методам (FM 2016), том 9995 LNCS, стр.291–309 (2016)
Менс, И.-Э., Малер, О.: Изучение обычных языков по крупным упорядоченным алфавитам. Бревно. Методы вычисл. Sci. 11 (3) (2015). https://doi.org/10.2168/LMCS-11(3:13)2015
Argyros, G., Stais, I., Kiayias, A., Keromytis, AD: Снова в черном: к формальному , черный ящик анализ дезинфицирующих средств и фильтров. В: Симпозиум IEEE по безопасности и конфиденциальности, SP 2016, стр. 91–109 (2016)
Drews, S., D’Antoni, L.: Изучение символических автоматов. В: Инструменты и алгоритмы для построения и анализа систем — 23-я международная конференция, TACAS 2017, том 10205 LNCS, стр. 173–189 (2017)
Ланг, К.Дж., Перлмуттер, Б.А., Прайс, РА : Результаты конкурса abbadingo one dfa по обучению и новый алгоритм слияния состояний, основанный на фактических данных. В: Хонавар В., Слуцки Г. (ред.) Грамматический вывод. Шпрингер, Берлин (1998)
Google ученый
Walkinshaw, N., Lambeau, B., Damas, C., Bogdanov, K., Dupont, P .: Stamina: соревнование по поощрению разработки и оценки методов вывода моделей программного обеспечения. Эмпир. Софтв. Англ. 18 (4), 791–824 (2013)
Артикул Google ученый
Verwer, S., Eyraud, R., Higuera, C .: Pautomac: соревнование по обучению вероятностных автоматов и скрытых марковских моделей. Мах. Учиться. 96 (1), 129–154 (2014)
MathSciNet Статья Google ученый
Джаспер, М., Муес, М., Муртови, А., Шлютер, М., Ховар, Ф., Штеффен, Б., Шордан, М., Хендрикс, Д., Шиффелерс, Р., Куппенс, Х. , Vaandrager, FW: Rers 2019: сочетание синтеза с реальными моделями. В: Бейер, Д., Хейсман, М., Кордон, Ф., Штеффен, Б. (ред.) Инструменты и алгоритмы для построения и анализа систем, стр. 101–115. Springer International Publishing, Cham (2019)
Google ученый
Мур, Э.Ф .: Геданкен-эксперименты на последовательных машинах. В: Исследования автоматов, номер 34. Princeton University Press (1956)
Гилл, А .: Эксперименты по идентификации состояний в конечных автоматах. Инф. Контроль 4 , 132–154 (1961)
MathSciNet Статья Google ученый
Angluin, D .: Изучение регулярных множеств на основе запросов и контрпримеров. Инф. Comput. 75 (2), 87–106 (1987)
MathSciNet Статья Google ученый
Шахбаз, М., Гроз, Р .: Определение мучных машин. В: FM 2009, стр. 207–222 (2009)
Йонссон, Б .: Изучение моделей автоматов, расширенных данными. В: SFM 2011, Advanced Lectures, pp. 327–349 (2011)
Кассель, С., Ховар, Ф., Йонссон, Б., Штеффен, Б.: Изучение расширенных конечных автоматов. В: SEFM 2014, Proceedings, pp. 250–264 (2014)
Аартс, Ф., Вандрагер, Ф .: Обучение автоматов ввода-вывода. В: КОНКУР. Спрингер, стр.71–85 (2010)
Ховар, Ф., Штеффен, Б., Йонссон, Б., Кассель, С .: Вывод канонических регистровых автоматов. В: VMCAI 2012, Proceedings, pp. 251–266 (2012)
Аартс, Ф., Фитерау-Бростян, П., Куппенс, Х., Ваандрагер, Ф.У .: Автоматическое обучение регистров с новой генерацией значений. В: Теоретические аспекты вычислений — ICTAC, том 9399 LNCS, стр. 165–183 (2015)
Medhat, R., Ramesh, S., Bonakdarpour, B., Fischmeister, S.: Фреймворк для добычи гибридных автоматов из входных / выходных трасс. In: Embedded Software (EMSOFT), pp. 177–186 (2015)
Gold, E.M .: Сложность идентификации автоматов по заданным данным. Инф. Контроль 37 (3), 302–320 (1978)
MathSciNet Статья Google ученый
Heule, M.J., Verwer, S .: Синтез программной модели с использованием решателей выполнимости. Эмпир. Софтв. Англ. 18 (4), 825–856 (2013)
Артикул Google ученый
Ульянцев В., Закирзянов И., Шалыто А .: Предикаты нарушения симметрии на основе BFS для идентификации DFA. В: Теория языков и автоматов и приложения (LATA), том 8977 LNCS. Springer, стр. 611–622 (2015)
Ончина, Дж., Гарсия, П .: Определение обычных языков за полиномиальное время. В: Достижения в структурном и синтаксическом распознавании образов, стр. 99–108 (1992)
Дюпон, П .: Постепенный регулярный вывод. В: ICGI-96, pp. 222–237 (1996)
Лэнг, К.Дж., Перлмуттер, Б.А., Прайс, Р.А.: Результаты обучающего конкурса abbadingo one DFA и новый алгоритм слияния состояний, основанный на доказательствах. В: ICGI-98, стр. 1–12 (1998)
Бесчастных, И., Брун, Ю., Эрнст, М.Д., Кришнамурти, А.: Вывод моделей параллельных систем из журналов их поведения с помощью csight. В: Материалы 36-й Международной конференции по разработке программного обеспечения, ICSE 2014. ACM, Нью-Йорк, Нью-Йорк, США, стр. 468–479 (2014)
Verwer, S., de Weerdt, M., Witteveen, C .: Тест отношения правдоподобия для идентификации вероятностных детерминированных автоматов реального времени на основе положительных данных. В: Семпере, Дж. М., Гарсия, П. (ред.) Грамматический вывод: теоретические результаты и приложения, стр. 203–216. Шпрингер, Берлин (2010)
Google ученый
Уолкиншоу, Н., Тейлор, Р., Деррик, Дж .: Вывод расширенных моделей конечных автоматов из выполнения программного обеспечения.Эмпир. Софтв. Англ. 21 (3), 811–853 (2016). https://doi.org/10.1007/s10664-015-9367-7
Статья Google ученый
Спичакова, М .: Подход к выводу конечных автоматов, основанный на алгоритме поиска, основанном на гравитации. Proc. Эстонская Акад. Sci. 62 (1), 39–46 (2013)
Статья Google ученый
Александров, А.В., Казаков, С.В., Сергушичев, А.А., Царев, Ф.Н., Шалыто, А.А .: Использование эволюционного программирования на основе обучающих примеров для генерации конечных автоматов для управления объектами со сложным поведением. J. Comput. Sys. Sc. Int. 52 (3), 410–425 (2013)
Артикул Google ученый
Бужинский, И.П., Ульянцев, В.И., Чивилихин, Д.С., Шалыто, А.А.: Выведение конечных автоматов из обучающих выборок с использованием оптимизации муравьиной колонии.J. Comput. Sys. Sc. Int. 53 (2), 256–266 (2014)
Статья Google ученый
Мейнке, К .: CGE: алгоритм последовательного обучения для мучнистых автоматов. В: Семпере, Дж. М., Гарсия, П. (ред.) Грамматический вывод: теоретические результаты и приложения, 10-й международный коллоквиум, ICGI 2010, Валенсия, Испания, 13–16 сентября 2010 г. Труды, том 6339 LNCS. Springer, стр. 148–162 (2010)
Veelenturf, L.P.J .: Вывод последовательных машин из выборочных вычислений. IEEE Trans. Comput. 27 (2), 167–170 (1978)
MathSciNet Статья Google ученый
Takahashi, K., Fujiyoshi, A., Kasai, T .: алгоритм полиномиального времени для вывода последовательных машин. Syst. Comput. Jpn. 34 (1), 59–67 (2003)
Статья Google ученый
Бирманн, А.В., Фельдман, Дж. А .: О синтезе конечных автоматов на основе образцов их поведения. IEEE Trans. Comput. 21 (6), 592–597 (1972)
MathSciNet Статья Google ученый
Картик, А.В., Рэй, С., Нуццо, П., Мищенко, А., Брайтон, Р., Ройчоудхури, Дж .: ABCD-NL: аппроксимация непрерывных нелинейных динамических систем с использованием чисто булевых моделей для проверки аналоговых / смешанных сигналов.В: ASP-DAC, стр. 250–255 (2014)
Гринчтейн О., Лейкер М .: Изучение конечных автоматов у неопытных учителей. В: ICGI, стр. 344–345 (2006)
Leucker, M., Neider, D .: Изучение минимальных детерминированных автоматов у неопытных учителей. В: ISoLA, стр. 524–538 (2012)
Хейтмейер, К.Л., Пикетт, М., Леонард, Э.И., Арчер, М.М., Рэй, И., Ага, Д.У., Трафтон, Дж. обеспечение систем принятия решений, ориентированных на человека.Автомат. Софтв. Англ. 22 (2), 159–197 (2015)
Статья Google ученый
Ульянцев В., Бужинский И., Шалыто А .: Точная идентификация конечного автомата по сценариям и временным свойствам. СТТТ 20 (1), 35–55 (2018)
Статья Google ученый
Гулвани, С., Шривастава, С., Венкатесан, Р .: Программный анализ как решение ограничений.В: PLDI’08. ACM, pp. 281–292 (2008)
Колон, М.А., Санкаранараянан, С., Сипма, Х.Б .: Линейная инвариантная генерация с использованием решения нелинейных ограничений. В: CAV. Springer, pp. 420–432 (2003)
Гупта А., Рыбальченко А .: Invgen: эффективный инвариантный генератор. В: Компьютерная проверка, CAV. Springer, pp. 634–640 (2009)
Ackermann, C., Cleaveland, R., Huang, S., Ray, A., Shelton, C., Latronico, E .: Автоматическое извлечение требований из тестовые случаи.В: Проверка времени выполнения, RV’10 (2010)
Джин, Х., Донц, А., Дешмук, Дж. В., Сешия, С. А.: Требования к добыче из моделей управления с обратной связью. IEEE Trans. Comput. Помощь Дес. Интегр. Circuits Syst. 34 (11), 1704–1717 (2015)
Статья Google ученый
Lemieux, C., Park, D., Beschastnikh, I .: Разработка общих технических условий LTL. В: Автоматизированная разработка программного обеспечения (ASE), стр. 81–92 (2015)
Аммонс, Г., Бодик, Р., Ларус, Дж. Р.: Характеристики горных работ. В: POPL’02. ACM, pp. 4–16 (2002)
Ли, Д., Яннакакис, М .: Принципы и методы тестирования конечных автоматов — обзор. Proc. IEEE 84 (8), 1090–1123 (1996)
Статья Google ученый

 Менее популярны автоматы с характеристиками B и D, в основном на этих трех группах и строится токовая защита бытовых сетей. Но есть автоматы и с другими характеристиками.
Менее популярны автоматы с характеристиками B и D, в основном на этих трех группах и строится токовая защита бытовых сетей. Но есть автоматы и с другими характеристиками. Посмотрите на следующую картинку, обратите внимание на разброс параметров тепловой защиты автоматических выключателей. Видите два числа сверху графика? Это очень важные числа. 1.13 — это та кратность, ниже которой никакой исправный автомат никогда не сработает. 1.45 — это та кратность, при которой любой исправный автомат гарантированно сработает. Что они означают на деле? Рассмотрим на примере. Возьмем автомат на 10А. Если мы пропустим через него ток 11.3А или меньше, он не отключится никогда. Если мы увеличим ток до 12, 13 или 14 А — наш автомат может через какое-то время отключиться, а может и не отключиться вовсе. И только когда ток превысит значение 14.5А, мы можем гарантировать, что автомат отключится. Насколько быстро — зависит от конкретного экземпляра. Например, при токе 15А время срабатывания может составлять от 40 секунд до 5 минут. Поэтому, когда кто-то жалуется, что у него 16-амперный автомат не срабатывает на 20 амперах, он это делает напрасно — автомат совершенно не обязан срабатывать при такой кратности. Более того — эти графики и цифры нормированы для температуры окружающей среды, равной 30°C, при более низкой температуре график смещается вправо, при более высокой — влево.
Посмотрите на следующую картинку, обратите внимание на разброс параметров тепловой защиты автоматических выключателей. Видите два числа сверху графика? Это очень важные числа. 1.13 — это та кратность, ниже которой никакой исправный автомат никогда не сработает. 1.45 — это та кратность, при которой любой исправный автомат гарантированно сработает. Что они означают на деле? Рассмотрим на примере. Возьмем автомат на 10А. Если мы пропустим через него ток 11.3А или меньше, он не отключится никогда. Если мы увеличим ток до 12, 13 или 14 А — наш автомат может через какое-то время отключиться, а может и не отключиться вовсе. И только когда ток превысит значение 14.5А, мы можем гарантировать, что автомат отключится. Насколько быстро — зависит от конкретного экземпляра. Например, при токе 15А время срабатывания может составлять от 40 секунд до 5 минут. Поэтому, когда кто-то жалуется, что у него 16-амперный автомат не срабатывает на 20 амперах, он это делает напрасно — автомат совершенно не обязан срабатывать при такой кратности. Более того — эти графики и цифры нормированы для температуры окружающей среды, равной 30°C, при более низкой температуре график смещается вправо, при более высокой — влево.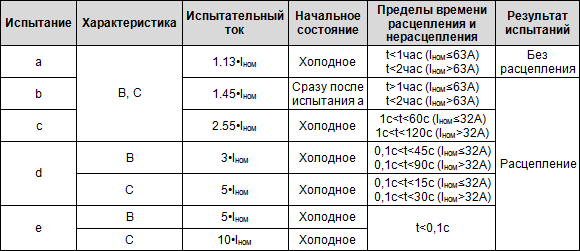 Но далеко не факт, что ток короткого замыкания в нашей цепи где-нибудь на дальней розетке будет достаточен для срабатывания отсечки. Конечно, через десяток секунд тепловой расцепитель нагреется и отключит цепь, но для проводки это окажется серьезным испытанием, да и возгорание в месте замыкания может произойти. Поэтому нужно искать компромисс. Как показала практика, для защиты розеток в жилых помещениях, офисах — там, где не предполагается использование мощного электроинструмента, промышленного оборудования, — лучше всего устанавливать автоматы группы B. Для кухни и хозблока, для гаражей и мастерских обычно ставятся автоматы с характеристикой C — там, где есть достаточно мощные трансформаторы, электродвигатели, там есть и пусковые токи. Автоматы группы D следует ставить там, где есть оборудование с тяжелыми условиями пуска — транспортеры, лифты, подъемники, станки и т.д.
Но далеко не факт, что ток короткого замыкания в нашей цепи где-нибудь на дальней розетке будет достаточен для срабатывания отсечки. Конечно, через десяток секунд тепловой расцепитель нагреется и отключит цепь, но для проводки это окажется серьезным испытанием, да и возгорание в месте замыкания может произойти. Поэтому нужно искать компромисс. Как показала практика, для защиты розеток в жилых помещениях, офисах — там, где не предполагается использование мощного электроинструмента, промышленного оборудования, — лучше всего устанавливать автоматы группы B. Для кухни и хозблока, для гаражей и мастерских обычно ставятся автоматы с характеристикой C — там, где есть достаточно мощные трансформаторы, электродвигатели, там есть и пусковые токи. Автоматы группы D следует ставить там, где есть оборудование с тяжелыми условиями пуска — транспортеры, лифты, подъемники, станки и т.д. Ниже приведены характеристики E и K для селективных автоматических выключателей серии S750DR фирмы ABB:
Ниже приведены характеристики E и K для селективных автоматических выключателей серии S750DR фирмы ABB: д.)
д.)