Матрицы зануление: Определитель матрицы.

Определитель матрицы.

Навигация по странице:

Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.

Определение.

Определителем матрицы n×n будет число:

det(A) =	Σ	(-1)N(α1,α2,…,αn)·aα11·aα22·…·aαnn
	(α1,α2,…,αn)

где (α₁,α₂,…,α_n) — перестановка чисел от 1 до n, N(α₁,α₂,…,α_n) — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Свойства определителя матрицы

2. Определитель матрицы с двумя равными строками (столбцами) равен нулю.

3. Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.

4. Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.

5. Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.

6. При транспонировании значение определителя матрицы не меняется:

   det(A) = det(A^T)

7. Определитель обратной матрицы:

   det(A^-1) = det(A)^-1

8. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.

9. Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).

10. Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.

11. Общий множитель в строке (столбце) можно выносить за знак определителя:

    a₁₁a₁₂. ..a_1na₂₁a₂₂…a_2n….k·a_i1k·a_i2…k·a_in….a_n1a_n2…a_nn = k·a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….a_i1a_i2…a_in….a_n1a_n2…a_nn

12. Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:

    B = k·A   =>   det(B) = kⁿ·det(A)

    где A матрица n×n, k — число.
13. Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:

    a₁₁a₁₂…a_1na₂₁a₂₂. ..a_2n….b_i1 + c_i1b_i2 + c_i2…b_in + c_in….a_n1a_n2…a_nn = a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….b_i1b_i2…b_in….a_n1a_n2…a_nn + a₁₁a₁₂…a_1na₂₁a₂₂…a_2n….c_i1

    c_i2…c_in….a_n1a_n2…a_nn

14. Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

15. Определитель произведения матриц равен произведению определителей этих матриц:

    det(A·B) = det(A)·det(B)

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Правило:

Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:

∆ = |a₁₁| = a₁₁

Вычисление определителя матрицы 2×2

Правило:

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

= a11·a22 — a12·a21

Пример 1.

Найти определитель матрицы A

A =

5 7 -4 1

Решение:

det(A) =

= 5·1 — 7·(-4) = 5 + 28 = 33

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило:

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

+		–

∆ =

a11 a12 a13 a21 a22 a23 a31 a32 a33

=

=  a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ — a₁₃·a₂₂·a₃₁ — a₁₁·a₂₃·a₃₂ — a₁₂·a₂₁·a₃₃

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Правило:

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:

∆ =

a11 a12 a13 a11 a12 a21 a22 a23 a21 a22 a31 a32 a33 a31 a32

=

=  a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ — a₁₃·a₂₂·a₃₁ — a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Пример 2.

Найти определитель матрицы A = 571-410203

Решение:

det(A) = 571-410203 = 5·1·3 + 7·0·2 + 1·(-4)·0 — 1·1·2 — 5·0·0 — 7·(-4)·3 = 15 + 0 + 0 — 2 — 0 + 84 = 97

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Правило:

Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

	n
det(A) =	Σ	aij·Aij	— разложение по i-той строке
	j = 1

Правило:

Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

	n
det(A) =	Σ	aij·Aij	— разложение по j-тому столбцу
	i = 1

При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.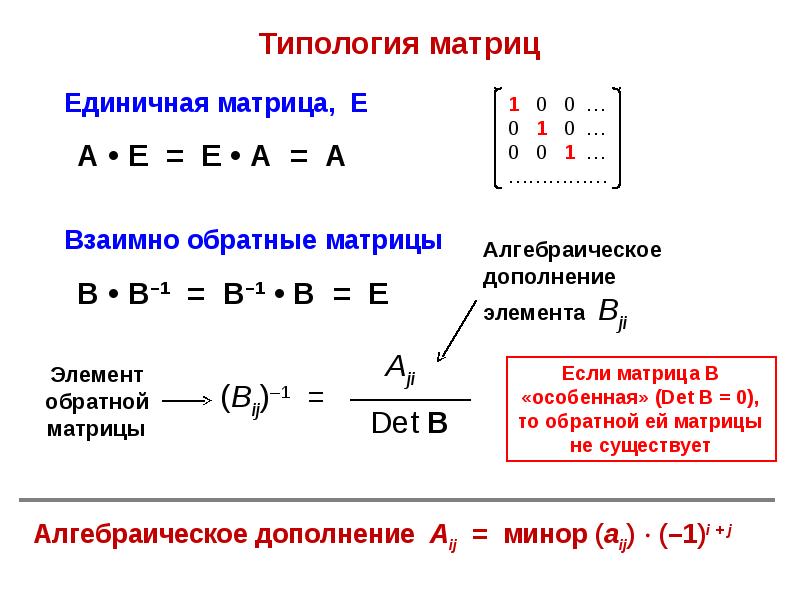

Пример 3.

Найти определитель матрицы A

A =	2 4 1 0 2 1 2 1 1

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

= 2·(-1)¹⁺¹· 2111 + 0·(-1)²⁺¹· 4111 + 2·(-1)³⁺¹· 4121 =

= 2·(2·1 — 1·1) + 2·(4·1 — 2·1) = 2·(2 — 1) + 2·(4 — 2) = 2·1 + 2·2 = 2 + 4 = 6

Пример 4.

Найти определитель матрицы A

A = 2411020021134023

Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):

det(A) = 2411020021134023 = — 0· 411113023 + 2· 211213423 — 0· 241213403 + 0· 241211402 =

= 2·(2·1·3 + 1·3·4 + 1·2·2 — 1·1·4 — 2·3·2 — 1·2·3) = 2·(6 +12 + 4 — 4 — 12 — 6) = 2·0 = 0

Приведение определителя к треугольному виду

Правило:

Используя свойства определителя для элементарных преобразований над строками и столбцами 8 — 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.

Пример 5.

Найти определитель матрицы A приведением его к треугольному виду

A = 2411021021134023

Решение:

det(A) = 2411021021134023

Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:

det(A) = 241102102 — 21 — 41 — 13 — 14 — 2·20 — 4·22 — 1·23 — 1·2 = 241102100-3020-801

Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):

det(A) = — 2141012000-3200-81

Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:

det(A) = — 214 + 1·81012 + 0·8000-3 + 2·8200-8 + 1·81 = — 211210120001320001 = -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Пусть ∆ — определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Присоединяйтесь

© 2011-2020 Довжик Михаил
Копирование материалов запрещено.

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]

Защитное зануление: устройство, назначение, принцип действия

Зануление, применяемое в электросетях, подразделяется на рабочее и защитное. Если рабочее зануление, согласно п. 1.7.33 ПУЭ (см. Главу 1.7), выполнено посредством рабочего проводника N и имеет электрическую связь с такими элементами электросети, как глухозаземленная нейтраль генератора или трансформатора (трехфазная сеть), с глухозаземленным выводом источника (однофазная сеть постоянного тока), с глухозаземленной точкой источника (однофазная сеть постоянного тока), то защитное зануление выполнено посредством защитного проводника PE и имеет электрическую связь с этими же элементами электрической сети, что и рабочее зануление. Рабочее зануление предназначено для обеспечения процесса электроснабжения, а защитное выполняет функции электробезопасности (п. 1.7.34 ПУЭ) или «защитного заземления». В различных случаях для защиты от действия электрического тока может применяться либо защитное зануление либо защитное заземление. Так, например, последнее применяется для защиты от действия электрического тока при косвенном прикосновении (п.1.7.51 ПУЭ). В этой статье мы подробно рассмотрим, что такое зануление, для чего оно нужно и как работает.

Принцип действия

Работа защитного зануления и защитного заземления отличаются тем, что при занулении, если на корпусе оборудования появляется опасный потенциал, то может случиться короткое замыкание. Под действием тока короткого замыкания в несколько раз большего по значению, чем номинальный ток сети, срабатывает предохранитель или другой защитный аппарат. При защитном заземлении поражающее действие электрического тока нейтрализуется снижением величины напряжения прикосновения (и напряжения шага) до безопасного значения. Поврежденный бытовой электроприбор или электрооборудование, не имеющие защитных зануления или заземления, могут долгое время находиться под напряжением и стать опасными для человека в момент касания или при приближении к оборудованию на опасное расстояние.

Как сказано выше, при попадании фазы на корпус прибора, который выполнен из металла и соединен с нулевым защитным проводником, происходит короткое замыкание. Величина тока короткого замыкания больше в несколько раз величины номинального тока. Под его воздействием срабатывают аппараты защиты. Вследствие этого отключаются электрические линии, подключенные через защитный аппарат.

Площадь сечения проводников следует выбирать исходя из требований соответствующих глав ПУЭ. Для защитных проводников ПУЭ (п. 1.7.5) определяет зависимость их сечения от сечения фазных проводников. Так для площадей сечений проводников фазы, меньших 16 мм², размер площади сечения защитного проводника равен площади сечения защитного проводника. Если площадь сечения фазного проводника находится в диапазоне от 16 до 35 мм², то площадь сечения защитного проводника равна 16 мм² и если площадь сечения фазного проводника больше 35 мм², то площадь защитного проводника выбирается в 2 раза меньше. Также площадь сечения можно рассчитать самостоятельно на основании этого же пункта ПУЭ. Главное условие выбора — обеспечить быстродействие, которое рассчитывается по формуле:

S≥ I*√t/k,

В этой формуле отражена прямая зависимость значения площади поперечного сечения защитного проводника (S) от значения тока короткого замыкания, при котором обеспечивается быстродействие защитных аппаратов в соответствии с табл.1.7.1 ПУЭ и 1.7.2 ПУЭ или за время не более 5 с в соответствии с 1.7.79 ПУЭ и значения времени срабатывания защитного аппарата (t). Обратная зависимость от значения коэффициента, который определяется материалом защитного проводника, его изоляции, начальной и конечной температурами проводника. Значение k для защитных проводников в различных условиях даны в табл.1.7.6-1.7.9 ПУЭ.

Схема ниже повторяет ранее указанный принцип действия и применение системы защитного зануления.

Назначение такого устройства обеспечить быстрое отключение неисправного электрооборудования от электропитания, тем самым нейтрализовать поражающее действие электрического тока при касании человеком неисправного прибора.

Схема работы системы зануления в случае пробоя изоляции, изображена ниже:

Узнать, в чем разница между занулением и заземлением, вы можете из нашей статьи!

Область применения

Защитное зануление применяется в трехфазных сетях переменного тока и однофазных сетях переменного и постоянного тока, уровень напряжения которых до 1000 В.

Если электрическая сеть трехфазная переменного тока и уровень напряжения составляет 660/380В, 380/220В или 220/127В, то заземляется нулевой проводник — сеть типа TN.

Если сеть однофазная переменного тока, то защитное зануление применяется при условии, что заземлен вывод сети.

Если сеть однофазная постоянного тока, то защитное заземление используется, если заземлена средняя точка источника электрической энергии.

Защитное зануление может выполняться как с помощью РЕ проводников, так и с помощью совмещенного РЕN проводника. Применение того или иного вида защитного зануления зависит от того, какая система заземления используется в электроустановке и какой величины площадь сечения питающих кабелей.

Согласно п 1.7.131 ПУЭ, может объединяться функционал нулевого защитного и нулевого рабочего проводников при условии, что они используются в многофазных цепях в системе TN и проложены стационарно. При этом должны соблюдаться требования по обеспечению площади поперечного сечения жил проводников, изготовленных из разных материалов. Жилы медных кабелей должны иметь площадь поперечного сечения не менее 10 мм², жилы алюминиевых кабелей — не менее 16 мм².

П.1.7.132 ПУЭ запрещает в цепях однофазного и постоянного тока совмещать функционал нулевого защитного и нулевого рабочего проводников. Для защитного зануления используется отдельный третий проводник — исключением является ответвление от ВЛ напряжением до 1 кВ к однофазным потребителям электроэнергии.

Назначение

Защитное зануление применяется в качестве защиты от поражения электрическим током при эксплуатации электрооборудования различного назначения — бытового, производственного.

На рисунке выше нулевой защитный проводник системы TN-S обозначен PE. Показана токопроводящая цепь, соединяющая открытые токопроводящие поверхности и глухозаземленную нейтральную точку на источнике питания в трехфазной сети. Данная схема отражает назначение защитного нулевого проводника при заземлении нулевого защитного проводника в системе TN-S, когда применяется отдельный защитный проводник.

Если зануление применяется в системе TN-C, то схема будет выглядеть следующим образом:

В этом случае нулевой рабочий и нулевой защитный проводники объединены в одном PEN-проводнике.

А в этой трехфазной сети нулевой защитный проводник РЕ отделен от PEN проводника на вводе в электроустановку:

В системе постоянного тока заземляется средняя точка источника — рисунок ниже:

1 — заземлитель нейтрали (средней точки) в сети постоянного тока; 2 — открытые токопроводящие элементы сети; 3 — источник питания постоянного тока.

Во всех рассмотренных случаях защитный нулевой проводник выполняет защитную функцию, а в случае совмещения с рабочим проводником N в системе TN-C и функцию рабочего нулевого проводника.
Рекомендуем напоследок просмотреть полезное видео по теме:

Вот мы и рассмотрели устройство, принцип действия и назначение защитного зануления. Надеемся, теперь вам понятно как работает данная система и для чего она нужна.

Будет полезно прочитать:

Что такое защитное зануление — схема и принцип работы

Зануление представляет собой специальное подключение открытых металлических частей электрооборудования (электроустановок) к нейтрали. Это относится к металлическим не токоведущим частям оборудования, которые в нормальном (рабочем) режиме не находятся (и не должны находиться) под напряжением. Нейтраль, с которой происходит соединение, должна быть глухо заземлена.

В трёхфазных электрических сетях – это нейтраль генератора или силового трансформатора, в однофазной сети – это глухозаземлённый вывод источника питания.

Нулевым защитным проводником (не путать с нулевым рабочим проводником) является такой проводник, который соединяет металлические занулённые части электрооборудования с глухозаземлённой нейтралью, идущей от генератора или питающего силового трансформатора.

Цель защитного зануления – обеспечить электрическую безопасность в случае короткого замыкания на металлический корпус электрооборудования или электроустановки.

Принцип зануления

Защитное зануление работает следующим образом. Если при поданном электрическом питании происходит попадание фазы (случайное попадание или пробой изоляции фазного проводника) на металлический корпус с занулением, то возникает короткое замыкание, резко увеличивается значение электрического тока и срабатывает аппарат защиты (автоматический выключатель) или перегорает плавкая вставка защитного предохранителя, тем самым обесточивая электрооборудование или электроустановку.

Сопротивление защитного нулевого проводника должно быть очень низким. Это необходимо для того, чтобы обеспечить уровень тока короткого замыкания, достаточный для действия защиты. Т.е. значение тока к.з. должно быть достаточным для того, чтобы сработал защитный аппарат.

Если электрооборудование просто заземлить, то, например, в случае пробоя фазы на корпус ток короткого замыкания может быть недостаточным для того, чтобы сработал автоматический выключатель или перегорела плавкая вставка предохранителя.

Ввиду того, что нейтраль заземлена на генераторе или трансформаторе, благодаря защитному занулению обеспечивается достаточно малое напряжение прикосновения на корпусе. Т.е. защитное зануление можно считать своего рода разновидностью заземления.

Видео — Зануление и заземление — в чем разница?

Схемы защитного зануления

Существует несколько схем, по которым выполняется защитное зануление.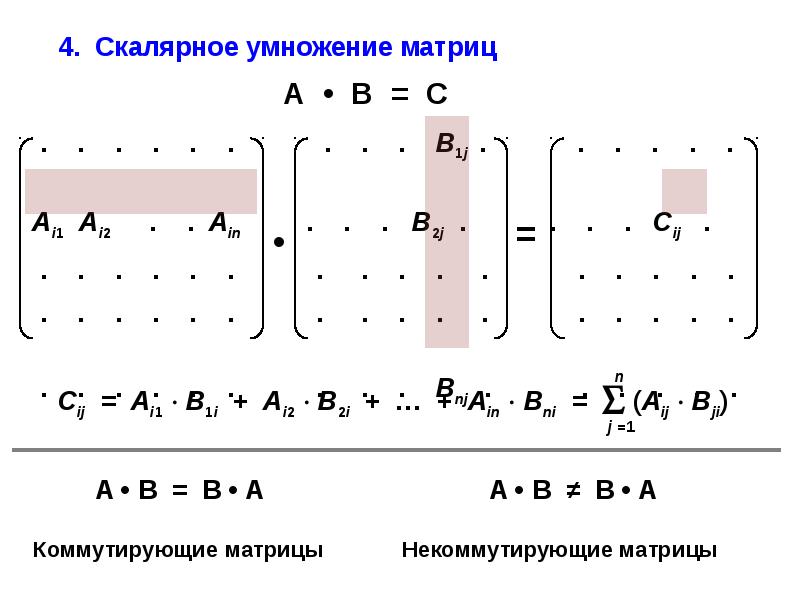

Система TN-C

Достаточно простая система, по которой выполняется защитное зануление. В ней нулевой проводник N и защитный проводник PE по всей длине объединены в один общий проводник PEN. Для реализации защитного зануления по системе TN-C необходимо соблюдать очень высокие требования к системе уравнивания потенциалов, а также к размеру поперечного сечения совмещённого PEN-проводника.

Зануление по системе TN-C применяется в трёхфазных электрических сетях, а в однофазных сетях такое зануление категорически запрещено.

Система TN-C-S

Данная система представляет собой соединённые N и PE проводники в части сети, начиная от электрического источника питания. По данной системе допускается зануление электрооборудования в однофазных сетях.

Область применения защитного зануления

Защитное зануление применяется в однофазных и трёхфазных сетях переменного тока до 1кВ. Сеть должна быть с глухозаземлённой нейтралью.

Проверка эффективности защитного зануления

Суть защитного зануления заключается в том, чтобы в случае короткого замыкания фазы на корпус электрооборудования произошло автоматическое отключение повреждённого участка цепи. Для того чтобы проверить на сколько эффективно выполнено защитное зануление, необходимо измерить сопротивление петли фаза-ноль в самой удалённой от источника питания точке. Это позволит определить, сработает ли аппарат защиты в случае однофазного к.з. на корпус.

Сопротивление петли фаза-ноль измеряется при помощи специальных измерительных приборов. Приборы для измерения петли фаза-ноль имеют два щупа. При измерении один щуп подключается к действующей фазе, а второй – к занулённой части электрооборудования.

В результате замера выясняется значение сопротивления петли фаза-ноль. Зная величину измеренного сопротивления и значение питающего напряжения, по формуле закона Ома для участка цепи можно рассчитать ток однофазного короткого замыкания, расчётное значение которого должно быть больше (или равно) тока срабатывания защитного устройства.

Допустим, для защиты цепи от токовых перегрузок и от коротких замыканий установлен автоматический выключатель, ток мгновенного срабатывания которого равен 100А. Измеренное значение сопротивления петли фаза-ноль равно 2 Ом, фазное напряжение в сети равно стандартному  значению 220В.

Рассчитываем значение тока однофазного короткого замыкания. По закону Ома I = U/R = 220В/2Ом = 110А.

Т.к. расчётный ток к.з. больше чем ток мгновенного срабатывания (отсечки) автоматического выключателя, то защитное зануление будет эффективным. Если бы расчетный ток к.з. получился меньше тока мгновенного срабатывания автомата, то для эффективности защитного зануления пришлось бы или менять автоматический выключатель на устройство с меньшим током срабатывания, или искать решение по уменьшению сопротивления петли фаза-ноль.

Очень часто в расчётах ток срабатывания автоматического выключателя умножается на так называемый коэффициент надёжности Кн или коэффициент запаса. Дело в том, что отсечка автомата не всегда соответствует указанному значению, т.е. может быть некоторая погрешность, для этого и вводится в расчёты указанный коэффициент. Для старых автоматов Кн может равняться, например, 1,25 или 1,4. Для новых современных автоматов он может быть равен 1,1. Это связано с тем, что новые аппараты защиты работают более точно.

Матрицы

— документация SymPy 1.7.1

 >>> из импорта sympy *
>>> init_printing (use_unicode = True)
 

Чтобы создать матрицу в SymPy, используйте объект Matrix . Матрица строится путем предоставления списка векторов-строк, составляющих матрицу. Например, построить матрицу

\ [\ begin {split} \ left [\ begin {array} {cc} 1 & -1 \\ 3 & 4 \\ 0 & 2 \ end {array} \ right] \ end {split} \]

используйте

 >>> Матрица ([[1, -1], [3, 4], [0, 2]])
⎡1 -1⎤
⎢ ⎥
⎢3 4 ⎥
⎢ ⎥
⎣0 2 ⎦
 

Чтобы упростить создание векторов столбцов, список элементов считается вектор-столбец.

 >>> Матрица ([1, 2, 3])
⎡1⎤
⎢ ⎥
⎢2⎥
⎢ ⎥
⎣3⎦
 

Матрицы

управляются так же, как и с любым другим объектом в SymPy или Python.

 >>> M = Матрица ([[1, 2, 3], [3, 2, 1]])
>>> N = Матрица ([0, 1, 1])
>>> М * Н
⎡5⎤
⎢ ⎥
⎣3⎦
 

В отношении матриц SymPy следует отметить одну важную вещь: в отличие от всех остальных объект в SymPy, они изменяемы. Это означает, что они могут быть изменены в место, как мы увидим ниже.Обратной стороной этого является то, что Matrix не может использоваться там, где требуется неизменяемость, например, внутри других SymPy выражения или как ключи к словарям. Если вам нужна неизменная версия Matrix , используйте ImmutableMatrix .

Основные операции

Форма

Вот некоторые основные операции на Matrix . Чтобы получить форму матрицы используйте форму

 >>> M = Матрица ([[1, 2, 3], [-2, 0, 4]])
>>> M
⎡1 2 3⎤
⎢ ⎥
⎣-2 0 4⎦
>>> М. форма
(2, 3)
 

Доступ к строкам и столбцам

Чтобы получить отдельную строку или столбец матрицы, используйте row или col . За Например, M.row (0) получит первую строку. M.col (-1) получит последний столбец.

 >>> М.роу (0)
[1 2 3]
>>> M.col (-1)
⎡3⎤
⎢ ⎥
⎣4⎦
 

Удаление и вставка строк и столбцов

Чтобы удалить строку или столбец, используйте row_del или col_del .Эти операции изменит матрицу вместо .

 >>> M.col_del (0)
>>> M
⎡2 3⎤
⎢ ⎥
⎣0 4⎦
>>> M.row_del (1)
>>> M
[2 3]
 

Чтобы вставить строки или столбцы, используйте row_insert или col_insert . Эти операции не работают на месте .

 >>> M
[2 3]
>>> M = M.row_insert (1, Матрица ([[0, 4]]))
>>> M
⎡2 3⎤
⎢ ⎥
⎣0 4⎦
>>> M = M.col_insert (0, Матрица ([1, -2]))
>>> M
⎡1 2 3⎤
⎢ ⎥
⎣-2 0 4⎦
 

Если явно не указано иное, указанные ниже методы не работают в место. Как правило, метод, который не работает на месте, вернет новый Матрица и метод, который работает на месте, вернут Нет .

Основные методы

Как отмечалось выше, выполняются простые операции, такие как сложение и умножение. просто используя + , * и ** .Чтобы найти обратную матрицу, просто возвести его в степень -1 .

 >>> M = Матрица ([[1, 3], [-2, 3]])
>>> N = Matrix ([[0, 3 

Онлайн-калькулятор обратной матрицы

Для любой неособой матрицы (т.е. определитель не равен нулю) существует обратная матрица , например, его произведение с исходной матрицей дает единичную матрицу:

А ∙ А ⁻¹ = А ⁻¹ ∙ А = E

Наш онлайн-калькулятор поддерживает два разных метода вычисления обратной матрицы: с помощью метода Гаусса-Жордана и с помощью составления алгебраических дополнений к исходной матрице.

Чтобы найти обратную матрицу методом Гаусса-Жордана, нужно прикрепить единичную матрицу справа от исходной матрицы:

(A | E)

Затем с помощью элементарных преобразований преобразуйте исходную матрицу в единичную, применив те же преобразования к единичной матрице, записанной справа. Следовательно, исходная матрица будет преобразована в единичную, а выписанная справа единичная матрица — в обратную:

(A | E) → (E | A ⁻¹ )

Этот способ прост, удобен и не требует больших затрат времени.

Чтобы найти обратную матрицу с помощью метода алгебраических дополнений, можно использовать следующую формулу:

где | А | — определитель матрицы A,
A _{i j} — алгебраическое дополнение элемента _и матрицы А.

По определению

A _{i j} = (-1) ^{i + j} M _{i j}

где M _{и J} — минор элемента _и матрицы А.

По определению — второстепенный элемент _и матрицы А — определитель, полученный удалением я строка, j столбец матрицы А.

Итак, алгебраический вспомогательный метод нахождения обратной матрицы исходной матрицы порядка п очень трудоемко, потому что нужно вычислить не только определитель исходной матрицы, но и n ² детерминанты порядка п-1 .

Калькулятор умножения матриц 3×3

Как найти произведение матриц $ n \ times n $?

Многие операции с матрицами имеют смысл только в том случае, если матрицы имеют подходящие размеры. Другими словами, они должны быть одинакового размера, с одинаковым количеством строк и одинаковым количеством столбцов.

Когда мы имеем дело с матричным умножением, матрицы $ A = (a_ {ij}) _ {m \ times p} $ с $ m $ строками, $ p $ столбцами и $ B = (b_ {ij}) _ {r \ times n} $ с $ r $ строками, $ n $ столбцов можно умножать тогда и только тогда, когда $ p = r $.Это означает, что количество столбцов первой матрицы $ A $ должно быть равно количеству строк второй матрицы $ B $. Результатом этой матрицы является новая матрица, которая имеет такое же количество строк, что и первая матрица, $ A $, и такое же количество столбцов, как вторая матрица, $ B $. Итак, соответствующее произведение $ C = A \ cdot B $ представляет собой матрицу размера $ m \ times n $. Элементами $ c_ {ij} $ этой матрицы являются $$ c_ {ij} = a_ {i1} b_ {1j} + a_ {i2} b_ {2j} \ ldots + a_ {ip} b_ {pj} \ quad \ mbox {for} \; i = 1, \ ldots , m, \; j = 1, \ ldots, n.$$ Например, умножение матриц $ 3 \ times 3 $ определяется по следующей формуле $$ \ begin {align} & \ left ( \ begin {array} {ccc} а_ {11} и а_ {12} и а_ {13} \\ а_ {21} и а_ {22} и а_ {23} \\ а_ {31} и а_ {32} и а_ {33} \\ \ end {массив} \ справа) \ cdot \слева( \ begin {array} {ccc} b_ {11} & b_ {12} & b_ {13} \\ b_ {21} & b_ {22} & b_ {23} \\ b_ {31} & b_ {32} & b_ {33} \\ \ end {массив} \ right) \\ & = \ left (\ begin {array} {ccc} a_ {11} b_ {11} + a_ {12} b_ {21} + a_ {13} b_ {31} и a_ {11} b_ {12} + a_ {12} b_ {22} + a_ {13} b_ {32} & a_ {11} b_ {13} + a_ {12} b_ {23} + a_ {13} b_ {33} \\ a_ {21} b_ {11} + a_ {22} b_ {21} + a_ {23} b_ {31} и a_ {21} b_ {12} + a_ {22} b_ {22} + a_ {23} b_ { 32} & a_ {21} b_ {13} + a_ {22} b_ {23} + a_ {23} b_ {33} \\ a_ {31} b_ {11} + a_ {32} b_ {21} + a_ {33} b_ {31} и a_ {31} b_ {12} + a_ {32} b_ {22} + a_ {33} b_ { 32} & a_ {31} b_ {13} + a_ {32} b_ {23} + a_ {33} b_ {33} \\ \ end {array} \ right) \ end {align} $$
Свойства умножения матриц

1. Умножение матриц, вообще говоря, не коммутативно, $ AB \ not BA $. В некоторых случаях возможно, что продукт $ AB $ существует, а продукт $ BA $ не существует. Оба произведения $ AB $ и $ BA $ определены тогда и только тогда, когда матрицы $ A $ и $ B $ являются квадратными матрицами одинакового размера.
2. Если $ A = (a_ {ij}) _ {mn} $, $ B = (b_ {ij}) _ {np} $ и $ C = (c_ {ij}) _ {pk} $, то матричное умножение ассоциативно, т.е. $$ A (BC) = (AB) C $$
3. Если $ A = (a_ {ij}) _ {mn} $, $ B = (b_ {ij}) _ {np} $, $ C = (c_ {ij}) _ {np} $ и $ D = (d_ {ij}) _ {pq} $, то умножение матриц дистрибутивно относительно сложения матриц, т.е.е. $$ \ begin {align} A (B + C) & = AB + AC \\ (B + C) D & = BD + CD \ end {align} $$
4. Если $ A_ {n \ times n} $ — квадратная матрица, существует единичная матрица $ I_ {n \ times n} $ такая, что $$ AI = IA = A $$

Например, найдем продукт $ AB $ для $$ A = \ left ( \ begin {array} {ccc} 10 и 20 и 10 \\ 4 и 5 и 6 \\ 2 и 3 и 5 \\ \ end {массив} \ right) \ quad \ mbox {и} \ quad B = \ left ( \ begin {array} {ccc} 3 и 2 и 4 \\ 3 и 3 и 9 \\ 4 и 4 и 2 \\ \ end {массив} \ right) $$ Используя формулу умножения матриц $ 3 \ times 3 $, произведение $ AB $ представляет собой матрицу $$ \ begin {align} C & = \ left ( \ begin {array} {ccc} 10 \ cdot3 + 20 \ cdot3 + 10 \ cdot4 & 10 \ cdot2 + 20 \ cdot3 + 10 \ cdot4 & 10 \ cdot4 + 20 \ cdot9 + 10 \ cdot2 \\ 4 \ cdot3 + 5 \ cdot3 + 6 \ cdot4 & 4 \ cdot2 + 5 \ cdot3 + 6 \ cdot4 & 4 \ cdot4 + 5 \ cdot9 + 6 \ cdot2 \\ 2 \ cdot3 + 3 \ cdot3 + 5 \ cdot4 & 2 \ cdot2 + 3 \ cdot3 + 5 \ cdot4 & 2 \ cdot4 + 3 \ cdot9 + 5 \ cdot2 \\ \ end {массив} \ справа) \\ & = \ left ( \ begin {array} {ccc} 130 и 120 и 240 \\ 51 и 47 и 73 \\ 35 и 33 и 45 \\ \ end {массив} \ right) \ end {align} $$

Работа матричного умножения с пошаговыми инструкциями показывает полное пошаговое вычисление для нахождение произведения $ AB $ двух $ 3 \ times 3 $ матриц $ A $ и $ B $ с использованием формулы умножения матриц.