Длина окружности, формула как найти длину окружности
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
l=πd, где
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как обозначается длина окружности?
Длина окружности обозначается буквой .
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
l=2πr , где
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
, где
π — число пи, примерно равное 3,14
S — площадь круга
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
l=πd, где
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
l=πa, где
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
, где
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
, где
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольникаКак вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
, где
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
(см)
Ответ: 15,7 (см)
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною дм
Решение. Радиус окружности равен . Подставим туда наши переменные и получим (дм).
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус , мы можем подставить наши данные и получить решение задачи.
Так и сделаем:
(дм)
Ответ: (дм)
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Формулы длины дуги. Длина дуги формула.
- Альфашкола
- Статьи
- Формулы длины дуги
Длина дуги — это расстояние вдоль части окружности, которая образует дугу. \(NM-\)длина дуги.
Измерение дуги в градусах
Длину окружности можно рассчитать следующим образом. Надо вычислить длину окружности, а затем умножить на меру дуги и
разделить полученный результат на \(360°\). Не забываем мера дуги равна величине центрального угла. Формулы длины дуги окружности:
\(L=\frac{2π r n}{360°}=\frac{π r n}{180°} \)
где \(r\)-радиус окружности, а \(n\)-мера дуги (или центрального угла) в градусах.
Радиус дуги r:
Центральный угол в радиусах n:
Если измерение дуги (или центрального угла) задано в радианах, то формула для длины дуги окружности является произведением радиуса и измерения дуги.
\(L= r × n\)
Радиус дуги r:
Мера дуги n:
где \(r\)-радиус окружности, а \(n\)-мера дуги (или центрального угла) в градусах.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Владислав Вадимович Мохныч
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный технический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 6-11 классов. Обществознание важно изучать каждому человеку, ведь оно дает дает фундаментальные знания о жизни человека в обществе, принципах взаимодействия людей друг с другом, государством, а также о внутреннем мире человека.
В своей работе я использую репродуктивный метод, метод проблемного изложения, а также внедряю на занятиях элементы исследования.
Своей любимой методикой могу назвать «Перевернутый класс» или » Сингапурскую методику».
Буду рад увидеть вас на моих занятиях. Я помогу вам освоить не только базовую школьную программу и подготовить к экзаменам, но и помогу освоить углубленные знания, которые пригодятся вам не только в ВУЗе или колледже, но и в обычной жизни.
Обществознание важно изучать каждому человеку, ведь оно дает дает фундаментальные знания о жизни человека в обществе, принципах взаимодействия людей друг с другом, государством, а также о внутреннем мире человека.
В своей работе я использую репродуктивный метод, метод проблемного изложения, а также внедряю на занятиях элементы исследования.
Своей любимой методикой могу назвать «Перевернутый класс» или » Сингапурскую методику».
Буду рад увидеть вас на моих занятиях. Я помогу вам освоить не только базовую школьную программу и подготовить к экзаменам, но и помогу освоить углубленные знания, которые пригодятся вам не только в ВУЗе или колледже, но и в обычной жизни.
Аида Робертовна Алтунян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Учитель первой категории. Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. Объясняю доступно, ясно, легко. Учитываю личность, характер ученика. К каждому ученику нахожу индивидуальный подход.
Учитель первой категории. Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива. Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. Объясняю доступно, ясно, легко. Учитываю личность, характер ученика. К каждому ученику нахожу индивидуальный подход.
Севиль Эннановна Калафатова
Репетитор по математике
Стаж (лет)
Образование:
Крымский федеральный университет им. Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов по математике (ВПР/ОГЭ), 5-8 классы по физике (ВПР).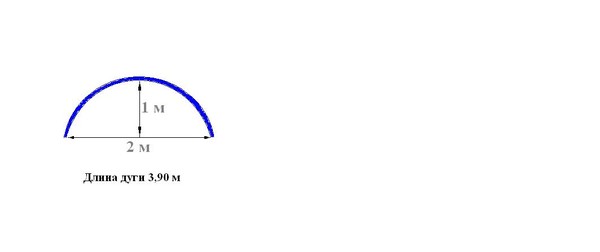 Развитие логического и аналитического мышления, дисциплина ума — следствия изучения математики. Буду рада помочь успешно усвоить материал школьной программы. Стану другом и наставником для вашего ребёнка! Приглашаю каждого на занятия!
Развитие логического и аналитического мышления, дисциплина ума — следствия изучения математики. Буду рада помочь успешно усвоить материал школьной программы. Стану другом и наставником для вашего ребёнка! Приглашаю каждого на занятия!
Похожие статьи
- Десятичные дроби
- Правильный шестиугольник
- Как легко разделить на 0,25
- Высшая Школа Бизнеса МГУ: стоимость обучения и проходной балл
- НИЯУ МИФИ: Факультет Экономики
- РУДН: Ландшафтная Архитектура
- Летнее меню: рацион школьника летом
- Я внучка (внук): взаимоотношения с бабушками и дедушками
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Калькулятор длины дуги
Создано Bogna Szyk
Отзыв Стивена Вудинга и Джека Боуотера
Последнее обновление: 11 марта 2022 г.
- Формула длины дуги
- Площадь сектора круга чтобы найти длину дуги и площадь сектора: пример
- Часто задаваемые вопросы
Этот калькулятор длины дуги представляет собой инструмент, который может рассчитать длину дуги и площадь сектора круга. В этой статье подробно объясняется формула длины дуги и приводятся пошаговые инструкции о том, как найти длину дуги. Вы также узнаете уравнение площади сектора.
Если вы новичок в кругах, вычисление длины и площади секторов может быть немного сложным, и вам нужно начать с более простых инструментов, таких как длина круга и длина окружности и площадь круга калькуляторы.
Формула длины дуги
Длина дуги зависит от радиуса окружности и центрального угла θ . Мы знаем, что для угла, равного 360 градусам (2π), длина дуги равна длине окружности. Следовательно, поскольку пропорция между углом и длиной дуги постоянна, мы можем сказать, что:
L / θ = C / 2π AS окружность C = 2πr ,
L / θ = 2πr / 2π L / θ = R L = r * θ Следовательно, длина дуги равна радиусу, умноженному на центральный угол (в радианах).
Площадь сектора круга
Аналогичным образом можно найти площадь сектора круга. Мы знаем, что площадь всего круга равна πr². Из пропорций
A / θ = πr² / 2π A / θ = r² / 2 Формула площади сектора: длина дуги и площадь сектора: пример
- Определите радиус окружности. Например, она может быть равна 15 см. (Вы также можете ввести диаметр в калькулятор длины дуги.)
- Какой будет угол между концами дуги? Допустим, он равен 45 градусам, или π/4.
- Рассчитайте длину дуги по приведенной выше формуле:
L = r * θ = 15 * π/4 = 11,78 см. - Вычислите площадь сектора:
A = r² * θ / 2 = 15² * π/4 / 2 = 88,36 см². - Вы также можете использовать калькулятор длины дуги, чтобы найти центральный угол или радиус окружности. Просто введите любые два значения в соответствующие поля и посмотрите, как он проведет все расчеты за вас.
Не забудьте также воспользоваться калькулятором уравнения окружности!
Часто задаваемые вопросы
Как найти длину дуги без радиуса?
Чтобы вычислить длину дуги без радиуса, вам нужен центральный угол и площадь сектора :
- Умножьте площадь на 2 и разделите результат на центральный угол в радианах.

- Найдите квадратный корень из этого деления.
- Умножьте этот корень на центральный угол еще раз, чтобы получить длину дуги.
- Единицы будут квадратным корнем из единиц площади сектора.
Или центральный угол и длина хорды :
- Разделите центральный угол в радианах на 2 и выполните для него функцию синуса.
- Разделите длину хорды на удвоенный результат шага 1. Это вычисление даст вам радиус.
- Умножьте радиус на центральный угол, чтобы получить длину дуги.
Как найти длину дуги в радианах?
- Умножьте центральный угол в радианах на радиус окружности.
- Вот оно! Результатом является просто это умножение.
Как рассчитать длину дуги без угла?
Чтобы рассчитать длину дуги без угла, вам нужен радиус и площадь сектора :
- Умножьте площадь на 2.
- Затем разделите результат на квадрат радиуса (убедитесь, что единицы измерения совпадают), чтобы получить центральный угол в радианах.

Или вы можете использовать радиус и длину хорды :
- Разделите длину хорды на удвоенный радиус.
- Найдите арксинус результата (в радианах).
- Удвойте результат обратного синуса, чтобы получить центральный угол в радианах.
- Получив центральный угол в радианах, умножьте его на радиус, чтобы получить длину дуги.
Должна ли длина дуги быть в радианах?
Длина дуги является мерой расстояния, поэтому она не может быть выражена в радианах . Однако центральный угол не обязательно должен быть в радианах. Это может быть любая единица измерения углов, от градусов до угловых секунд. Использование радианов , однако, намного проще для вычислений относительно длины дуги, так как найти его так же просто, как умножить угол на радиус.
Bogna Szyk
Центральный угол (θ)
Радиус (R)
Диаметр
Площадь сектора (A)
Длина хорды (C)
Длина дугиДлина дуги (l)
Проверка
Длина дуги
Длина дуга (l)
Проверка
Длина дуги из 8 подобных калькуляторов кругов ⭕Площадь кругаРасчет окружности: найти c, d, a, rОкружность… 5 еще
геометрия — Как рассчитать радиус сегмента дуги, зная только длину дуги и высоту сегмента дуги?
Спросил
Изменено 8 месяцев назад
Просмотрено 3к раз
$\begingroup$
Большинство вычислений, которые я знаю и могу найти, могут решить для радиуса, если известны длина шнура или угол вместе с высотой сегмента дуги. Однако я не могу найти и понять, как рассчитать радиус, если известны только сегмент дуги и высота сегмента.
Однако я не могу найти и понять, как рассчитать радиус, если известны только сегмент дуги и высота сегмента.
Я просмотрел несколько разных методов на этом и других сайтах, и следующие похожи, но не совсем то, что я ищу.
- Вычислить радиус окружности, зная длину хорды и высоту сегмента
- Вычисление высоты сегмента окружности во всех точках, если только длины хорды и дуги)
В САПР я могу нарисовать дугу, как показано на (http://mathworld.wolfram.com/CircularSegment.html). Если я фиксирую среднюю точку на (0,0), устанавливаю шнур горизонтально, затем добавляю размер высоты сегмента (т.е. h=2″) и затем измеряю длину дуги (т.е. s=10″), геометрия полностью стеснен. Поэтому я знаю, что есть способ решить эту проблему.
Если бы я поменял местами входные данные и знал длину дуги (s) и радиус (R), я мог бы рассчитать высоту сегмента, но у меня возникли проблемы с обращением уравнения.
- геометрия
- тригонометрия
$\endgroup$
1
$\begingroup$
Как ответил Аретино, вам нужны численные методы для решения уравнения $$L\big(1-\cos(\theta)\big)=2H\theta$$ (помните, что нет аналитического решения для $x= \cos(x)$). 92}}{2 \lambda }$$ Теперь выполните одну итерацию метода Ньютона, используя точное уравнение; это приведет к $$\theta_1=\frac{\theta_0 \lambda +\cos (\theta_0)-1}{\sin (\theta_0)-\lambda}+\theta_0$$ Для иллюстрации, используя $\lambda= \frac 25$, как и раньше, это приводит к $$\theta_0\приблизительно 0,846955$$ $$\theta_1\приблизительно 0,849961$$, в то время как точное решение будет $\приблизительно 0,849952$. Продолжая итерации для многих других фигур, итерации будут
$$\слева(
\begin{массив}{cc}
п & \тета_п \\
0 и 0,846954969749869 \\
1 и 0,849960525069669 \\
2 & 0,849952018812858 \\
3 и 0,849952018744878
\конец{массив}
\right)$$, что является решением для пятнадцати значащих цифр.
92}}{2 \lambda }$$ Теперь выполните одну итерацию метода Ньютона, используя точное уравнение; это приведет к $$\theta_1=\frac{\theta_0 \lambda +\cos (\theta_0)-1}{\sin (\theta_0)-\lambda}+\theta_0$$ Для иллюстрации, используя $\lambda= \frac 25$, как и раньше, это приводит к $$\theta_0\приблизительно 0,846955$$ $$\theta_1\приблизительно 0,849961$$, в то время как точное решение будет $\приблизительно 0,849952$. Продолжая итерации для многих других фигур, итерации будут
$$\слева(
\begin{массив}{cc}
п & \тета_п \\
0 и 0,846954969749869 \\
1 и 0,849960525069669 \\
2 & 0,849952018812858 \\
3 и 0,849952018744878
\конец{массив}
\right)$$, что является решением для пятнадцати значащих цифр.
$\endgroup$
$\begingroup$
Если $2\theta$ — это угол, относящийся к данной дуге, имеющей длину $l$, радиус $r$ и высоту $h$, то у вас есть $l=2\theta r$ и $h=r(1 -\cos\тета)$. Исключив $r$, вы получите $l(1-\cos\theta)=2h\theta$, что в общем случае можно решить относительно $\theta$ только численно.


