Как определить радиус дуги или сегмента круга и найти центр
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье «Расчет арочной перемычки», поэтому здесь лишь приведу основные формулы:
tg(a/4) = 2Н/L (278.1.2)
тогда
а/4 = arctg(2H/L)
R = H/(1 — cos(a/2)) (278.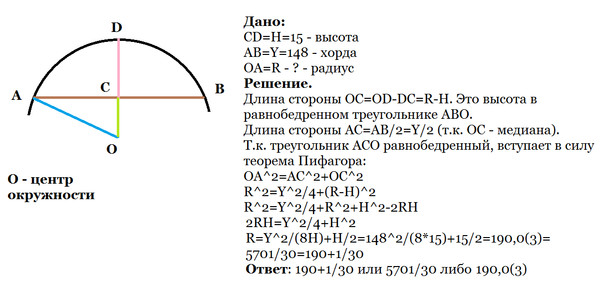
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад — для того, чтобы напомнить формулы — есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.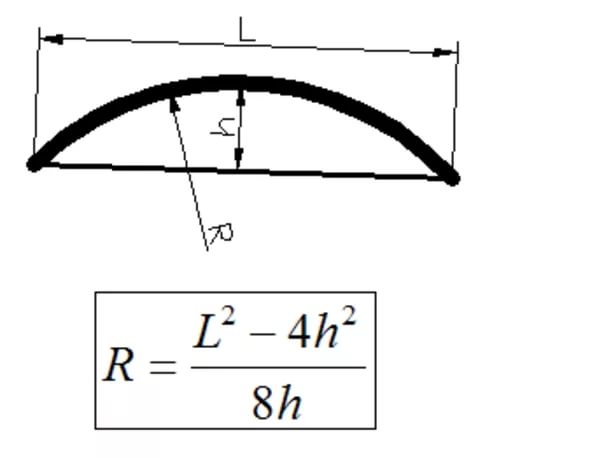
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Второй метод определения радиуса дуги (метод последовательных приближений)
Итак продолжим рассмотрение имеющейся ситуации.
Так как нам все равно необходимо найти центр окружности, то для начала мы из точек, соответствующих началу и концу дуги, проведем как минимум две дуги произвольного радиуса. Через пересечение этих дуг будет проходить прямая, на которой и находится центр искомой окружности.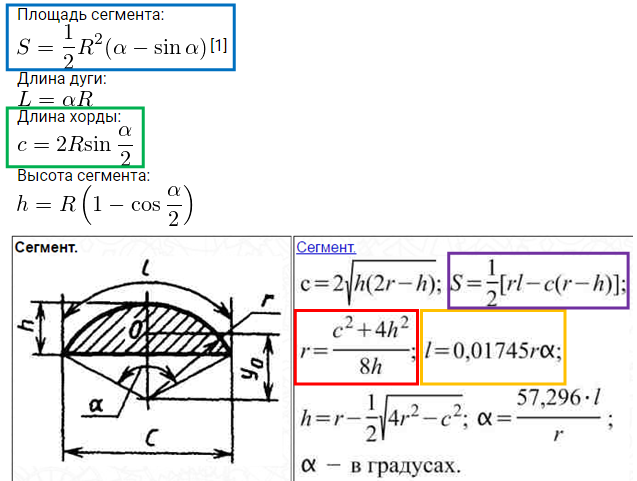
Теперь нужно соединить пересечение дуг с серединой хорды. Впрочем, если мы из указанных точек проведем не по одной дуге, а по две, то данная прямая будет проходить через пересечение этих дуг и тогда искать середину хорды вовсе не обязательно.
Ну а дальше все просто: измеряем расстояние от пересечения дуг до начала (или конца) рассматриваемой дуги, а затем расстояние от пересечения дуг до точки, соответствующей высоте сегмента.
Если расстояние от пересечения дуг до начала или конца рассматриваемой дуги больше, чем расстояние от пересечения дуг до точки, соответствующей высоте сегмента, то значит центр рассматриваемой дуги находится ниже на прямой, проведенной через пересечение дуг и середину хорды. Если меньше — то искомый центр дуги выше на прямой.
Исходя из этого на прямой принимается следующая точка, предположительно соответствующая центру дуги, и от нее производятся те же измерения. Затем принимается следующая точка и измерения повторяются.
С каждой новой точкой разница измерений будет все меньше.
Вот собственно и все. Не смотря на столь пространное и мудреное описание, для определения радиуса дуги таким способом с точностью до 1 мм достаточно 1-2 минут.
Теоретически это выглядит примерно так:
Рисунок 463.2. Определение центра дуги методом последовательных приближений.
А на практике примерно так:
Фотография 463.1. Разметка заготовки сложной формы с разными радиусами.
Тут только добавлю, что иногда приходится находить и чертить несколько радиусов, потому на фотографии так много всего и намешано.
Площадь сектора круга — формулы и примеры расчетов
Выполняя инженерные расчёты при проектировании различных объектов строительства, создании роботов, автоматизированных систем, станков, машин, самолётов, ракет, современных средств вооружения часто бывает необходимо найти площадь сектора круга.
Геометрия помогает при этом решать задачи на нахождение центра тяжести (центр масс), вычислять его координаты для плоских пластин, имеющих, в частности, форму правильного многоугольника.
Измерять и вычислять величины считается базовым умением. Оно включено в первую часть профильной программы выпускного экзамена ЕГЭ и ОГЭ по математике.
Сектор круга
Существует несколько определений, каждое из которых отличается только формулировкой, не меняющей подход к рассмотрению понятия:
-
Часть плоскости, ограниченная центральным углом и соответствующей дугой окружности.
-
Часть круга, заключённая между двумя радиусами.
Часто эту формулировку заменяют похожей, описывающей построение непосредственно: часть круга, лежащего внутри соответствующего центрального угла.
Площадь сектора круга через радиус и длину дуги
Пусть известны радиус круга R, длина дуги l.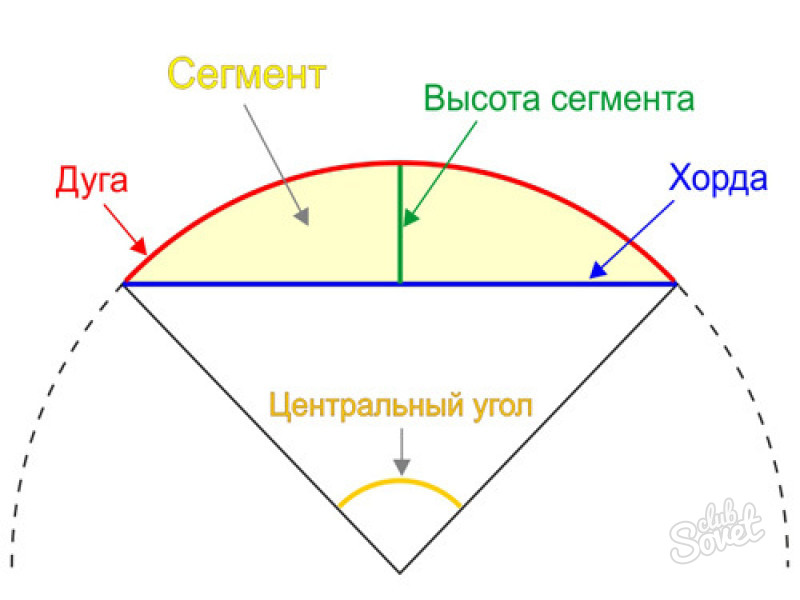
Как в этом случае определить площадь сектора, стягиваемого данной дугой?
Для ответа на вопрос понадобится формула нахождения длины окружности:
C = 2πR.
Определение, представленное через третью формулировку, даёт возможность соотнести численные величины понятий: сектор и круг, дуга и окружность, центральный и полный углы.
Поскольку отношения постоянны, то для ответа на поставленный вопрос достаточно найти отношение части к целому, затем умножить полученный результат на площадь круга S = πR2.
После сокращения дроби получают формулу:
Примеры решения задач
Задача №1
Найти площадь сектора круга радиусом 2 см, имеющего длину дуги 4 см.
Решение.
Подставляя имеющиеся величины в формулу, получаем:
Sсект = (4 * 2) / 2 = 4.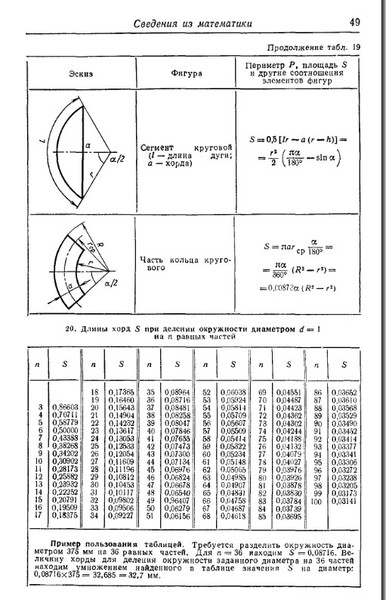
Ответ: Sсект = 4 см2.
Задача №2
Чему равна длина дуги закрашенного сектора, если Sсект = 32 см2, R = 4 см.Решение.
Подставив известные данные в формулу, получим:
Следовательно,
2l = 32,
l = 16.
Тот же результат получился бы при первоначальной работе в «общем виде»:
Ответ: l = 16 см.
Площадь сектора круга через радиус и угол сектора
Если известна градусная мера центрального угла (n°), то, находя отношение её к полному кругу (к 360º), также умножают результат на площадь круга:
Задача №3
Чему равна площадь фигуры, изображённой на рисунке?Решение.
Центральный угол изображённого сектора равен
Подставляя в формулу величины, несложно получить искомый результат:
Ответ: Sсект = 27 см2.
Также аналогичным образом решаются обратные задачи.
Площадь сектора круга через угол сектора в радианах
Пусть центральный угол задан своей радианной мерой. Учитывая, что
несложно получить искомую формулу:
Задача №4
Чему равен центральный угол сектора в радианах (рад.), если его площадь равна 32, а радиус – 4?
Решение.
Выразив α, затем подставив числовые данные, легко получить результат:
Ответ: α = 4 рад.
Благодаря этой формуле, несложно доказать, что площади двух секторов с равными центральными углами относятся как квадраты радиусов соответствующих окружностей:
С другой стороны, площадь части кольца находится из условия:
youtube.com/embed/e6DxjJ3tkiw?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Сегмент круга
Существует два подхода к определению понятия:
-
Геометрическая фигура, являющаяся общей частью круга и полуплоскости, называется сегментом круга.
-
Часть плоскости, заключённая между хордой и окружностью.
Оба определения характеризуют один и тот же объект с разных сторон, выражая, по сути одно и то же.
Иногда проводится описательное построение. В этом случае второй вариант быстрее приводит к данному термину.
Площадь сегмента круга по хорде и высоте
Пусть градусная мера ограничивающей дуги мала, длина хорды равна a, h — высота сегмента (перпендикуляр, опущенный из точки на окружности к середине хорды).
Примечание: часто высота сегмента называется «стрелкой».
Тогда можно приближённо считать, что
Погрешность такого вычисления уменьшается вместе с отношением
.В частности, когда дуга содержит угол, меньший 50º, то есть,
погрешность оказывается менее 1%.
Более точной является формула для любого сегмента меньшего полукруга:
Точный расчёт производится, исходя из свойства нахождения сложной фигуры, являющейся суммой или разностью двух и более объектов.
Сегмент является частью сектора, к которому либо добавлен треугольник, содержащий центральный угол (для дуг больших 180º), либо убран (соответствующий центральный угол меньше 180º).
Отсюда следует, что
Задача №5
Вычислить стрелку и площадь сегмента, если центральный угол содержит 60º, а
.Решение.
Для нахождения стрелки достаточно из радиуса вычесть высоту треугольника AOB.
Поскольку угол AOB по условию равен 60º, то треугольник AOB равносторонний. Поэтому его высота в √3/2 раз отличается от стороны (от радиуса).
Отсюда следует, что:
Площадь по первой формуле будет приблизительно равна
По второй:
Применяя точную формулу и учитывая, что
находим:
Ответ: Sсегм = 1,26 см2.
Площадь сегмента круга через синус угла
Рассматривая точную формулу, площадь треугольника можно находить, используя половину произведения сторон на синус угла между ними. А значит:
Многие вычисления помогает провести онлайн калькулятор. Достаточно ввести исходные данные и запросить результат.
Как найти радиус по хорде
Хорда – это отрезок, соединяющий две точки окружности.
Пускай длина хорды знаменита. Тогда, если также знаменит угол между радиусами , проведенными в концы хорды, то дозволено обнаружить и радиус окружности.
Вам понадобится
- Транспортир, линейка.
Инструкция
1. Пускай вестимы длина хорды AB и угол AOB между радиусами , проведенными в концы хорды. Обнаружим по этим данным радиус окружности с центром в точке O.
2. Треугольник AOB – равнобедренный, потому что OA = OB = R. По свойству равнобедренного треугольника высота OE единовременно является его медианой и биссектрисой угла AOB. Обозначим угол AOB за х.Треугольник AEO – прямоугольный с прямым углом AEO. Потому что высота ОЕ также является биссектрисой угла AOB, то угол AOE = x/2. Тогда из прямоугольного треугольника AOE имеем: OA = R = (AB/2)/sin(x/2).
Если для многоугольника получается возвести вписанную и описанную окружности, то площадь этого многоугольника поменьше площади описанной окружности, но огромнее площади вписанной окружности.
1/2.
3. Для многоугольников не неизменно допустимо узнать соотношение радиусов вписанных и описанных окружностей и длин его сторон. Почаще ограничиваются построением таких окружностей около многоугольника, а после этого физического измерения радиуса окружностей с подмогой измерительных приборов либо векторного пространства.Для построения описанной окружности выпуклого многоугольника строят биссектрисы 2-х его углов, на их пересечении лежит центр описанной окружности. Радиусом будет расстояние от точки пересечения биссектрис до вершины всякого угла многоугольника. Центр вписанной окружности лежит на пересечении перпендикуляров, построенных вовнутрь многоугольника из центров сторон (эти перпендикуляры именуются срединными). Довольно возвести два таких перпендикуляра. Радиус вписанной окружности равен расстоянию от точки пересечения срединных перпендикуляров до стороны многоугольника.
Видео по теме 
com/embed/GdN3F5Pnh8k?wmode=transparent» frameborder=»0″ allowfullscreen=»»/>
Обратите внимание!
В произвольно данный многоугольник невозможно вписать окружность и описать окружность вокруг него.
Полезный совет
В четырехугольник дозволено вписать окружность, если a+c = b+d, где a, b, с, d – стороны четырехугольника по порядку. Вокруг четырехугольника дозволено описать окружность, если противоположные его углы в сумме дают 180 градусов;Для треугольника такие окружности неизменно существуют.
Найти радиус — Учеба и наука
ВОПРОС:
Здравствуйте! Можно ли найти радиус окружности по длине хорды и дуги? или нужны дополнительные данные?
ОТВЕТ:
Ничего дополнительного не нужно, решение задачи изложено ниже.
РЕШЕНИЕ:
Разделим исходный сектор круга, ограниченного центром круга и концами хорды, на два одинаковых, проведя биссектрису центрального угла.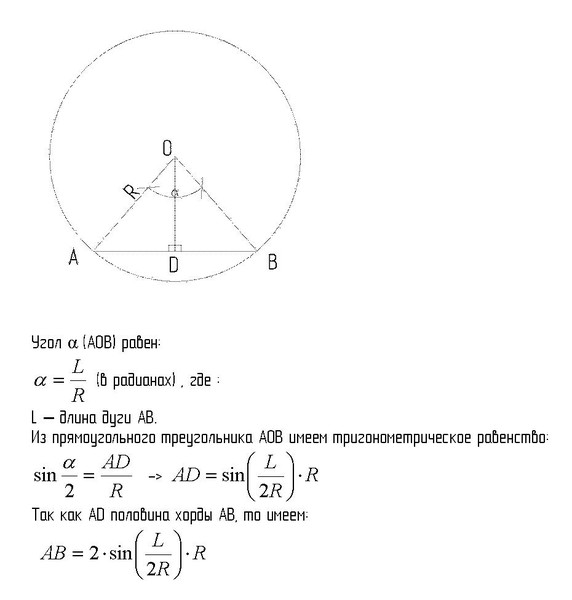
Будем рассматривать далее один из них (любой из двух полученных) и соответствующий прямоугольный треугольник (с вершинами в центре круга, одним из концов хорды и её серединой).
Пусть, далее, α – острый угол этого треугольника с вершиной в центре круга, a – длина противолежащей стороны (катета) этого треугольника, b — длины соответствующей дуги окружности, r – её радиус (искомый). Отметим также, что a и b – заданные величины, равные половине длин исходных хорды и дуги соответственно.
Тогда, очевидно (из чисто геометрического рассмотрения), имеем:
αr = b (1)
a/r = sin α (2)
Это, по сути, запись двух определений: (1) – для длины дуги, (2) – для синуса угла. Таким образом, имеем систему двух уравнений с двумя неизвестными (α и r). Явного (аналитического) решения она не имеет – возможно лишь численное решение (которое существует и единственно).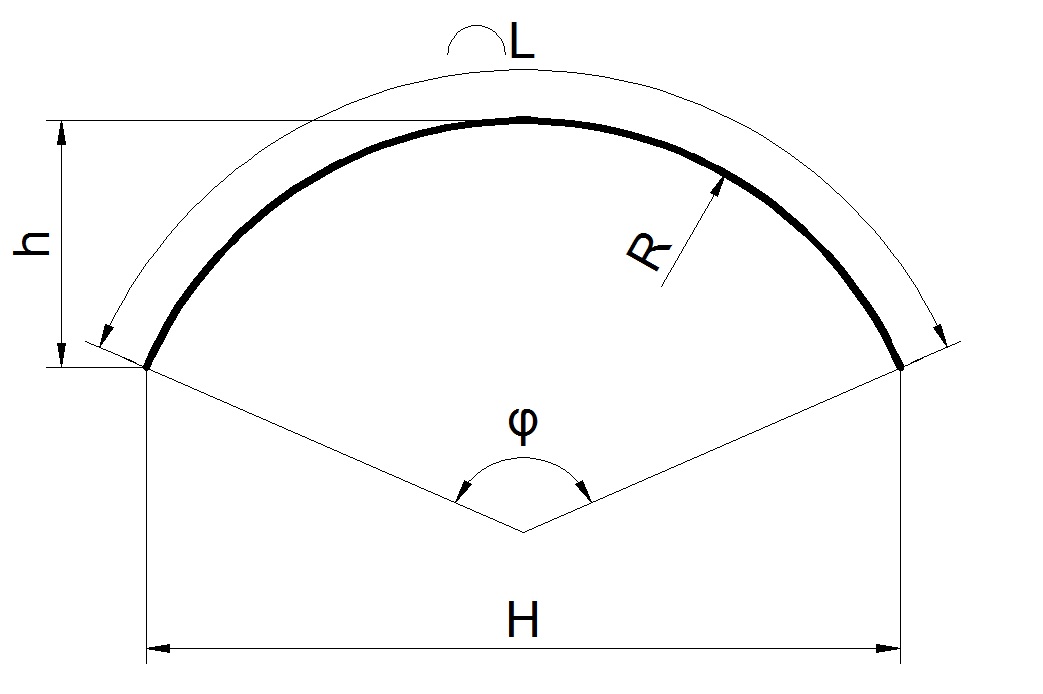
Решать эту задачу в каждом конкретном случае – при заданных численных значениях a и b (точнее, как отмечено выше, – 2a и 2b) – можно двумя способами: «школьным» (геометрическим) и каким-либо численным методом.
«Школьный» метод:
После несложных преобразований уравнения (1) и (2) можно переписать, например, в виде:
r = b/α (1′)
kα = sin α , (2′)
где k = a/b. После этого строим графики функций f1(α) = kα, f2(α) = sin α и находим точку их пересечения, что соответствует решению уравнения (2′).
Отметим, что это пересечение (т.е. решение задачи) существует и единственно (и находится «недалеко» от начала координат): оба графика проходят через начало координат, причем второй (синусоида) выходит из начала координат под углом π/4 (=45o), первый (прямая) – под меньшим углом (поскольку k = a/b < 1, т.
к. a < b – хорда должна быть короче дуги).
Таким образом, из графика находим α, а затем, используя уравнение (1′), и искомое значение радиуса r.
Численный метод:
Типичное численное решение такой задачи – каким-либо итерационным методом, например, методом Ньютона: дифференцируем и линеаризуем (по α) уравнение (2′), задаём какое-нибудь начальное приближение αo для α (наиболее логично и просто взять αo = 0) и дальше итерационно находим решение α = α* с любой наперед заданной точностью. Далее, подставляя в уравнение (1′) найденное значение угла α*, находим искомое значение радиуса r.
Можно чуть по-другому – чтобы сразу решать уравнение (задачу) относительно радиуса r (без промежуточного нахождения угла α = α*). Для этого, например, просто подставляем из (1) (или из (1′)) выражение для угла α = b/r в уравнение (2′), получив тогда уравнение относительно переменной r.
Далее также как и выше дифференцируем, линеаризуем (но уже не по α, а по r) и решаем полученное уравнение и задачу в целом.
Круг: сектор, сегмент. Площадь круга, сектора и сегмента
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
S = πr2,
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | )2 = π | D2 | = π | D2 | . |
| 2 | 22 | 4 |
Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr2 | · n = | πr2n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
можно представить в виде произведения
| πr2n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |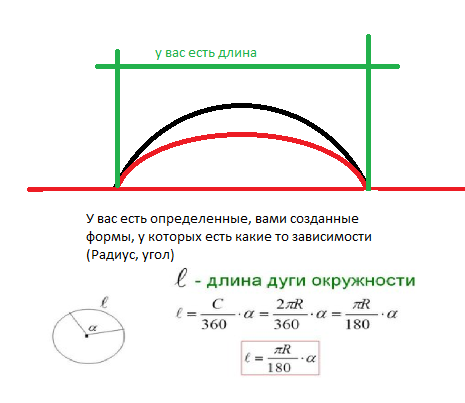
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Формула длины дуги через хорду – 4apple – взгляд на Apple глазами Гика
На практике часто требуется найти длину дуги, данной на чертеже или в натуре, причем неизвестно, какую часть окружности составляет дуга и каков ее радиус.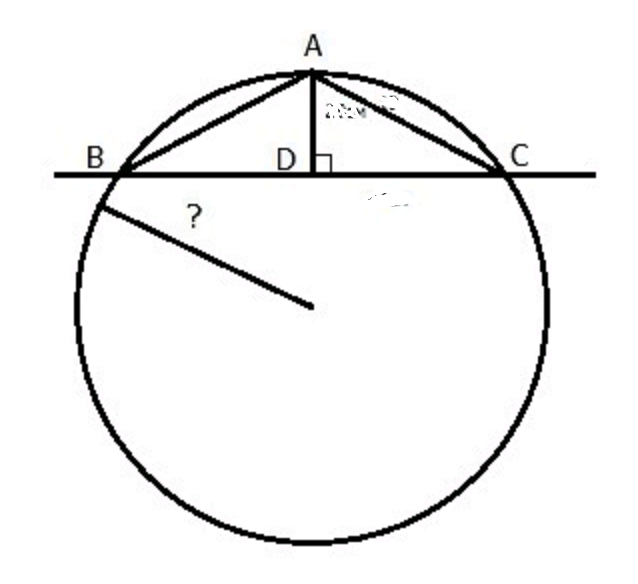
В таких случаях используют формулу Гюйгенса.
На дуге отмечают середину M. Она лежит на перпендикуляре СM, проведенном к хорде AB через середину хорды C. Далее измеряют хорды AB и AM. Длина дуги выражается через формулу Гюйгенса так:
Относительная погрешность этой формулы составляет 0.5%, когда дуга AB содержит 60°. С уменьшением угловой меры дуги процент погрешности резко падает. Для дуги в 45° относительная погрешность составляет примерно 0.02%.
Вычисляет площадь, длину дуги, длину хорды, высоту и периметр сегмента круга. Описывается несколько вариантов расчета по параметрам сегмента – по углу, по хорде, по радиусу, по высоте и длине дуги.
Сегмент кругаКруговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Сегмент
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см.
длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Гибочный калькулятор
Чаще всего стоит задача определения параметров дуги по её габаритным размерам. Для этого мы предлагаем гибочный калькулятор.
Введите значения H и h в миллиметрах
Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм.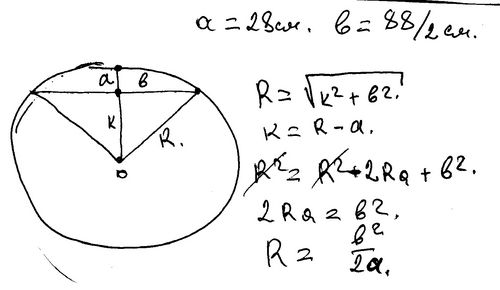
на заготовку.
Вы можете скачать ПК версию гибочного калькулятора по этой ссылке.
140030, МО, Люберецкий район, пос. Малаховка, Касимовское шоссе, д. 3Г
Право собственности ООО «ПК РАДИУС» © 2002–2017. Все права защищены.
Оцените статью: Поделитесь с друзьями!Определение Сагитты с помощью калькулятора — Math Open Reference
Определение Сагитты с помощью калькулятора — Math Open Reference Сагитта — это высота дуга.Это перпендикуляр от середины дуги. аккорд к самой дуге.
Попробуйте это Перетащите оранжевую точку, чтобы переместить аккорд. Обратите внимание, как пересчитывается сагитта.
На рисунке выше синяя дуга — это часть круга, отрезанная горизонтальной хордой.Сагитта — это вертикальная линия от середины хорды до самой дуги. Это мера «высоты» дуги.
Длина хорды, сагитты и радиус дуги взаимосвязаны, и если вы знаете любые два, вы можете рассчитать третий.
1.
Нахождение сагитты по радиусу и хорде
Нахождение сагитты по радиусу и хордеВы можете найти длину сагитты по формуле: где:
| с | — длина сагитты |
| r | — радиус дуги |
| л | — это одна половина расстояния по основанию дуги (половина длины хорды) |
Обратите внимание, что есть два результата из-за «плюса» или «минуса» в формуле.Меньшая — это сагитта, как показано на диаграмме выше. Другой — более длинная сагитта, которая проходит в противоположную сторону по большей части круга:
2. Нахождение сагитты по радиусу и длине дуги
Сделайте это в два этапа: Сначала найдите половину длины хорды, используя где:| а | — длина дуги |
| r | — радиус дуги |
| л | — это одна половина расстояния по основанию дуги (половина длины хорды) |
* Обратите внимание, что функция синуса должна рассчитываться в радианах.
3. Определение радиуса по стреле и хорде
Если вы знаете длину сагитты и ширину дуги (длину хорды), вы можете найти радиус по формуле: где:| с | — длина сагитты |
| r | — радиус дуги |
| л | — это одна половина расстояния по основанию дуги (половина длины хорды) |
4.Нахождение хорды по стреле и радиусу
Если вам известны сагитта и радиус дуги, вы можете найти ширину дуги (которая является длиной хорды) по формуле: где:| с | — длина сагитты |
| r | — радиус дуги |
| л | — это одна половина расстояния по основанию дуги (половина длины хорды) |
Примечание Во всех приведенных выше формулах длина l составляет половину ширины дуги.
Полная ширина будет вдвое больше.
Калькулятор
Введите радиус и длину хорды или длину дуги. Когда вы нажмете «рассчитать», будет рассчитана сагитта. Не забудьте использовать одни и те же единицы для всех входов.Что попробовать
- В приведенном выше апплете нажмите «Сброс» и «Скрыть детали».
- Перетащите оранжевую точку, чтобы изменить положение аккорда.
- Рассчитайте длину сагитты.
- Щелкните «Показать подробности», чтобы проверить результат.
Другие темы кружка
Общий
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Определение радиуса круга и калькулятор
Определение радиуса круга и калькулятор — Math Open Reference 1. Линия от центра круга до точки на окружности.
2. Расстояние от центра круга до точки на окружности.
Попробуйте это Перетащите оранжевую точку. Синяя линия всегда остается радиусом круга.
Радиус круга — это длина линии от центра до любой точки на его крае. Форма множественного числа — радиусы (произносится как «луч-ди-глаз»). На рисунке выше перетащите оранжевую точку и убедитесь, что радиус всегда постоянен в любой точке круга.
Иногда слово «радиус» используется для обозначения самой линии.В этом смысле вы можете увидеть «нарисовать радиус круга». В более позднем смысле это длина линии, поэтому ее называют «радиус круга составляет 1,7 сантиметра».
Если известен диаметр
Учитывая диаметр круга, радиус просто равен половине диаметра: где:D — диаметр окружности
Если знать окружность
Если вам известна длина окружности, радиус можно найти по формуле, где:
C — длина окружности
π — Пи, приблизительно 3.142
Если вы знаете район
Если вам известна площадь круга, радиус можно найти по формуле, где:
A — площадь круга
π — Пи, приблизительно 3,142
Калькулятор
Воспользуйтесь калькулятором выше, чтобы вычислить свойства круга.
Введите любое одно значение, и остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.
Точно так же, если вы войдете в область, будет вычислен радиус, необходимый для получения этой области, а также диаметр и окружность.
Сопутствующие товары
Диаметр Ширина круга. Диаметр в два раза больше радиуса. Посмотреть диаметр круга
Окружность Окружность — это расстояние по краю круга. Видеть Окружность круга для подробностей.
Что попробовать
- На рисунке выше нажмите «Сброс» и перетащите оранжевую точку.Обратите внимание, что радиус имеет одинаковую длину в любой точке круга.
- Щелкните «Показать диаметр». Перетащите любую оранжевую точку на концах линии диаметра. Обратите внимание на то, что радиус всегда равен половине диаметра.
- Снимите флажок «фиксированный размер». Повторите вышесказанное и обратите внимание на то, что радиус всегда равен половине диаметра, независимо от размера круга.
Другие темы кружка
Общий
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Проблема с хордой: найти радиус
Сегодня у меня была возможность решить настоящую математическую задачу, включающую в себя круг и хорд известной длины в нем. Пришлось найти радиус . Это была не задача из учебника или головоломка на каком-то веб-сайте, а математическая задача, которую мне нужно было решить для собственных нужд.Некоторое время я думал, что смогу найти ответ в Интернете, но я не нашел, поэтому я выписываю его на случай, если он понадобится кому-то другому — они смогут найти это решение, выполнив поиск в Интернете.
Я хотел создать в CorelDraw что-то вроде « форм луны» , чтобы использовать их в качестве водяных знаков в моих новых книгах. У меня есть высота и ширина «ленты».
Вот проблема математически:
У меня хорды круга длиной 17 мм в моем примере, а другое расстояние , отмеченное на изображении, составляет 5 мм. Мне нужно найти радиус круга И угловую меру дуги круга, которая делает скругленную часть ленты.
Сначала, как я уже сказал, я поискал, есть ли какая-нибудь теорема или формула, которые прямо скажут мне, что мне нужно. Я не нашел ни одного, но понял, что могу использовать эту теорему для решения своей проблемы:
Если две хорды пересекаются, произведение сегментов одной хорды равно произведению сегментов другой хорды ( см. доказательство).
Моя проблема выглядит так:
Моя хорда пересекает диаметр окружности, которая тоже является хордой.Две части первого шнура — 8,5 и 8,5, а две части другого — 5 и d -5. Таким образом, я получаю уравнение
5 ( d -5) = 8,5 2
Отсюда быстро получается, что d = 19,45. Тогда радиус, конечно, будет вдвое меньше, или 9,725.