Дельта т формула: Дельта T — это… Что такое Дельта T?

Дельта T — это… Что такое Дельта T?

Дельта T, ΔT, Delta T, delta-T, deltaT, или DT — обозначение временной разницы между земным временем (TT) и всемирным временем (UT).

Тонкости определения

В литературе, выпущенной в разное время могут встречаться немного отличающиеся определения ΔT (в зависимости от того, какая шкала равномерного времени была рекомендована для использования в астрономических расчетах в тот или иной период):

• ΔT=ET−UT (До 1984 года)
• ΔT=TDT−UT (с 1984 по 2001 годы)
• ΔT=TT−UT(с 2001 года по настоящее время).

Кроме того, под «Всемирным временем» может подразумеваться одна из его версий (UT0, UT1 и т. д.). Поэтому в специализированной литературе принято указывать, что имеется в виду под ΔT, например «DTD — UT1», что означает «Динамическое земное время минус Всемирное время версии UT1».

О неравномерности вращения Земли вокруг своей оси

Всемирное время (UT) является шкалой времени, основанной на суточном вращении Земли, которое не вполне равномерно на относительно коротких интервалах времени (от дней до столетий), и поэтому любые измерения времени, основанные на такой шкале не могут иметь точность лучше чем 1 : 10

⁸. Однако основной эффект проявляется на больших временах: на масштабах столетий приливное трение постепенно замедляет скорость вращения Земли примерно на 2,3 мс/сутки/век. Однако есть и другие причины, изменяющие скорость вращения Земли. Самой важной из них являются последствия таяния материкового ледникового щита в конце последнего ледникового периода. Это привело к уменьшению мощной нагрузки на земную кору и послеледниковой релаксации, сопровождающейся распрямлением и поднятием коры в приполярных областях — процесс, который продолжается и сейчас и будет продолжаться пока не будет достигнуто изостатическое равновесие. Этот эффект послеледниковой релаксации приводит к перемещению масс ближе к оси вращения Земли, что заставляет её вращаться быстрее (закон сохранения углового момента). Полученное из этой модели ускорение составляет около −0.6 мс/сутки/век. Таким образом, полное ускорение (на самом деле замедление) вращения Земли, или изменение длины средних солнечных суток составляет +1.7 мс/сутки/век. Эта величина хорошо соответствует среднему темпу замедления вращения Земли за последние 27 столетий.

[1]

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948-52^[2] с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на Солнечные таблицы (англ.)русск. Саймона Ньюкомба (1895), интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях.^[3]

Таблицы Ньюкомба служили основой для всех астрономических солнечных эфемерид с 1900 по 1983 год. Изначально они были выражены (и в таком виде опубликованы) в терминах среднего времени по Гринвичу и средних солнечных суток,

[4] однако позднее, в особенности в отношении периода с 1960 по 1983 г., они трактовались как выраженные в рамках ET,^[5] в соответствии с принятым в 1948-52 предложением о переходе к ET. В свою очередь, ET могло теперь рассматриваться в свете новых результатов^[6] как шкала времени максимально близкая к среднему солнечному времени на интервале 1750 и 1890 (с серединой около 1820 года), поскольку именно в этом интервале проводились наблюдения, на основании которых были составлены таблицы Ньюкомба. Хотя шкала TT является строго однородной (основана на единице секунды СИ, и каждая секунда строго равна каждой другой секунде), на практике она реализуется как Международное атомное время (TAI) с точностью около 1 : 10¹⁴.

Определение Дельта Т из наблюдений

Время, определяемое положением Земли (точнее, ориентацией Гринвичского меридиана относительно фиктивного среднего Солнца), является интегралом от скорости вращения. При интегрировании с учетом изменения длины суток на +1,7 мс/сутки/век и выборе начальной точки в 1820 году (примерная середина интервала наблюдений, использованных Ньюкомбом для определения длины суток), для ΔT получается в первом приближении парабола 31×((Год − 1820)/100)² в секунд. Сглаженные данные, полученные на основе анализа исторических данных о наблюдениях полных солнечных затмений дают значения ΔT около +16800 с в −500 году, +10600 с в 0, +5700 с в 500, +1600 с в 1000 и +180 с в 1500. Для времени после изобретения телескопа, ΔT определяются из наблюдений покрытий звезд Луной, что позволяет получить более точные и более частые значения величины. Поправка ΔT продолжала уменьшаться после 16 века, пока не достигла плато +11±6 с между 1680 и 1866 года. В течение трех десятилетий до 1902 она оставалась отрицаельной с минимумом −6,64 с, затем начала увеличиваться до +63,83 с в 2000 году. В будущем ΔT будет увеличиваться с нарастающей скоростью (квадратично). Это потребует добавления все большего числа секунд координации к Всемирному координированному времени (UTC), поскольку UTC должно поддерживаться с точностью в одну секунду относительно равномерной шкалы UT1. (Секунда СИ, используемая сейчас для UTC, уже в момент принятия была немного короче, чем текущее значение секунды среднего солнечного времени.

[7]) Физически нулевой меридиан для Универсального времени оказывается почти всегда восточнее меридиана Земного времени как в прошлом, так и в будущем. +16800 с или 4⅔ часа соответствуют to 70° в.д. Это означает, что в −500 году вследствие более быстрого вращения Земли солнечное затмение происходило на 70° восточнее положения, которое следует из расчетов с использованием равномерного времени TT.

Все значения ΔT до 1955 года зависят от наблюдений Луны, связанных либо с затмениями либо с покрытиями. Сохранение углового момента в Системе Земля-Луна требует, чтобы уменьшение углового момента Земли вследствие приливного трения передавался Луне, увеличивая её угловой момент, что означает, что её расстояние до Земли должно увеличиваться, что, в свою очередь, вследствие третьего закона Кеплера приводит к замедлению обращения Луны вокруг Земли. Приведенные выше значения ΔT предполагают, что ускорение Луны, связанное с этим эффектом составляет величину d

n/dt = −26″/век² , где n — средняя угловая сидерическая скорость Луны. Это близко к лучшим экспериментальным оценкам для dn/dt, полученным в 2002 году: −25.858±0.003″/век²^[8], и поэтому оценки ΔT, полученные ранее исходя из значения −26″/век², принимая во внимание неопределенности и эффекты сглаживания в экспериментальных наблюдениях, можно не пересчитывать. В наше время UT определяется по измерению ориентации Земли по отношению к инерциальной системе отсчета, связанной с внегалактическими радиоисточниками, с поправкой на принятое соотношение между сидерическим и солнечным временем. Эти измерения, проводимые в нескольких обсерваториях, координируются Международной службой вращения Земли (IERS).

Величины Дельта Т

ΔT на протяжении 1657—1984 гг.^[9]

Для 1900—1995 годов значения приведены согласно «Астрономия на персональном компьютере» четвёртое издание, 2002 год, Монтенбрук О., Пфеглер Т., для 2000 года — из английской Вики.

Год	Дельта Т
1900	-2.72
1905	3.86
1910	10.46
1915	17.20
1920	21.16
1925	23.62
1930	24.02
1935	23.93
1940	24.33
1945	26.77
1950	29.15
1955	31.07
1960	33.15
1965	35.73
1970	40.18
1975	45.48
1980	50.54
1985	54.34
1990	56.86
1995	60.82
2000	63.83
2005
2010

Приближенная формула для вычисления Дельта Т

С 1972 года по наше время ΔT можно расчитать зная количество секунд координации по формуле:

ΔT≈32.184+10+N

где

32.184 секунд — разница между TT и TAI

10 секунд — разница между TAI и UTC на начало 1972 года

N — количество введенных с 1972 года секунд координации

Формула дает погрешность не более 0.9 секунд. Например, на начало 1995 года было введено 19 секунд координации и формула дает ΔT=61.184 секунд, что лишь на 0.364 секунды превышает табличное значение.

См. также

Приливное ускорение

Примечания

1. ↑ McCarthy & Seidelmann 2009, 88-89
2. ↑ Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, Nautical Almanac Offices of UK and USA (1961), at pp.9 and 71.
3. ↑ См. предложение Г. М. Клеменса в его статье G. M. Clemence «On the System of Astronomical Constants», Astronomical Journal v.53 (1948), #1170, 169—179; а также G. M. Clemence, «The Concept of Ephemeris Time», Journal for the History of Astronomy v.2 (1971), 73-79 (рассказывает об истории принятия предложения эфемеридного времени).
4. ↑ См. Newcomb’s Tables of the Sun (Washington, 1895), Введение и Раздел I. Основания таблиц, c.9 и 20, ссылаются на единицы времени относительно среднего полудня по Гринвичу, по среднему времени по Гринвичу, в единицах средних солнечных суток: и W de Sitter, on p.38 of Bulletin of the Astronomical Institutes of the Netherlands, v4 (1927), pp.21-38, «On the secular accelerations and the fluctuations of the moon, the sun, Mercury and Venus», где «астрономическое время, задается вращением Земли и используется во всех практических астрономических расчетах», и подчеркивается, что оно «отличается от ‘однородного’ или ‘ньютоновского’ времени».
5. ↑ См. с. 612 в Explanatory Supplement to the Astronomical Almanac, ed. P K Seidelmann, 1992, где подтверждается использование ET в эфемеридах Альманаха, начиная с 1960 г. издания.
6. ↑ См. F. R. Stephenson (1997), и Stephenson & Morrison (1995), а также другие цитируемые ниже публикации.
7. ↑ :(1)»The Physical Basis of the Leap Second», by D D McCarthy, C Hackman and R A Nelson, Astronomical Journal, vol.136 (2008), 1906—1908: «the SI second is equivalent to an older measure of the second of UT1, which was too small to start with and further, as the duration of the UT1 second increases, the discrepancy widens.»: (2) В конце 1950х стал использоваться цезиевый стандарт, как для определения текущего значения секунды среднего солнечного времени (9192631830 периодов), так и для определения секунды эфемеридной шкалы (ET) (9192631770 +/-20 периодов), см. «Time Scales», by L. Essen, in Metrologia, vol.4 (1968), pp.161-165, on p.162. Для стандарта секунды СИ было выбрано значение 9192631770 периодов.
8. ↑ J.Chapront, M.Chapront-Touzé, G.Francou (2002): «A new determination of lunar orbital parameters, precession constant, and tidal acceleration from LLR measurements» (also in PDF). Astronomy & Astrophysics 387, 700—709
9. ↑ IERS Rapid Service/Prediction Center (c. 1986). Historic Delta T and LOD. Source attributed data to McCarthy and Babcock (1986) . Retrieved December 2009.

• McCarthy, D.D. & Seidelmann, P.K. TIME: From Earth Rotation to Atomic Physics. Weinheim: Wiley-VCH. (2009). ISBN 978-3-527-40780-4

• Stephenson, F.R. Historical Eclipses and Earth’s Rotation. Cambridge University Press, 1997. ISBN 0-521-46194-4

• Stephenson, F. R. & Morrison, L.V. «Long-term fluctuations in the Earth’s rotation: 700 BC to AD 1990». Philosophical Transactions of the Royal Society of London, Series A 351 (1995) 165—202. JSTOR link. Includes evidence that the ‘growth’ in Delta-T is being modified by an oscillation with a wavelength around 1500 years; if that is true, then during the next few centuries Delta-T values will increase more slowly than is envisaged.

Ссылки

Дельта T — Википедия. Что такое Дельта T

ΔT (дельта T, Delta T, delta-T, deltaT, или DT) — разница между земным временем (TT) и всемирным временем (UT).

Тонкости определения

В литературе, выпущенной в разное время, могут встречаться немного отличающиеся определения ΔT (в зависимости от того, какая шкала равномерного времени была рекомендована для использования в астрономических расчетах в тот или иной период):

• ΔT=ET−UT (до 1984 года)
• ΔT=TDT−UT (с 1984 по 2001 годы)
• ΔT=TT−UT(с 2001 года по настоящее время).

Кроме того, под «Всемирным временем» может подразумеваться одна из его версий (UT0, UT1 и т. д.). Поэтому в специализированной литературе принято указывать, что имеется в виду под ΔT, например «DTD — UT1», что означает «Динамическое земное время минус Всемирное время версии UT1».

Несмотря на некоторые изменения в определении, физический смысл ΔT не меняется — это разница между идеальным равномерно текущим временем и «временем», определённым по вращению Земли (которое замедляется, причём неравномерно).

О неравномерности вращения Земли вокруг своей оси

Всемирное время (UT) является шкалой времени, основанной на суточном вращении Земли, которое не вполне равномерно на относительно коротких интервалах времени (от дней до столетий), и поэтому любые измерения времени, основанные на такой шкале, не могут иметь точность лучше чем 1 : 10⁸. Однако основной эффект проявляется на больших временах: на масштабах столетий приливное трение постепенно замедляет скорость вращения Земли примерно на 2,3 мс/сутки/век. Однако есть и другие причины, изменяющие скорость вращения Земли. Самой важной из них являются последствия таяния материкового ледникового щита в конце последнего ледникового периода. Это привело к уменьшению мощной нагрузки на земную кору и послеледниковой релаксации, сопровождающейся распрямлением и поднятием коры в приполярных областях — процесс, который продолжается и сейчас и будет продолжаться пока не будет достигнуто изостатическое равновесие. Этот эффект послеледниковой релаксации приводит к перемещению масс ближе к оси вращения Земли, что заставляет её вращаться быстрее (закон сохранения углового момента). Полученное из этой модели ускорение составляет около −0,6 мс/сутки/век. Таким образом, полное ускорение (на самом деле замедление) вращения Земли, или изменение длины средних солнечных суток составляет +1,7 мс/сутки/век. Эта величина хорошо соответствует среднему темпу замедления вращения Земли за последние 27 столетий.^[1]

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948-52^[2] с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на солнечные таблицы (англ.)русск. Саймона Ньюкома (1895), интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях.^[3]

Таблицы Ньюкома служили основой для всех астрономических солнечных эфемерид с 1900 по 1983 год. Изначально они были выражены (и в таком виде опубликованы) в терминах среднего времени по Гринвичу и средних солнечных суток,^[4] однако позднее, в особенности в отношении периода с 1960 по 1983 г., они трактовались как выраженные в рамках ET,^[5] в соответствии с принятым в 1948-52 предложением о переходе к ET. В свою очередь, ET могло теперь рассматриваться в свете новых результатов^[6] как шкала времени максимально близкая к среднему солнечному времени на интервале 1750 и 1890 (с серединой около 1820 года), поскольку именно в этом интервале проводились наблюдения, на основании которых были составлены таблицы Ньюкома. Хотя шкала TT является строго однородной (основана на единице секунды СИ, и каждая секунда строго равна каждой другой секунде), на практике она реализуется как Международное атомное время (TAI) с точностью около 1 : 10¹⁴.

Определение дельта Т из наблюдений

Время, определяемое положением Земли (точнее, ориентацией Гринвичского меридиана относительно фиктивного среднего Солнца), является интегралом от скорости вращения. При интегрировании с учётом изменения длины суток на +1,7 мс/сутки/век и выборе начальной точки в 1820 году (примерная середина интервала наблюдений, использованных Ньюкомом для определения длины суток), для ΔT получается в первом приближении парабола 31×((Год − 1820)/100)² в секунд. Сглаженные данные, полученные на основе анализа исторических данных о наблюдениях полных солнечных затмений дают значения ΔT около +16800 с в −500 году, +10600 с в 0, +5700 с в 500, +1600 с в 1000 и +180 с в 1500. Для времени после изобретения телескопа ΔT определяются из наблюдений покрытий звезд Луной, что позволяет получить более точные и более частые значения величины. Поправка ΔT продолжала уменьшаться после 16 века, пока не достигла плато +11±6 с между 1680 и 1866 года. В течение трех десятилетий до 1902 она оставалась отрицательной с минимумом −6,64 с, затем начала увеличиваться до +63,83 с в 2000 году. В будущем ΔT будет увеличиваться с нарастающей скоростью (квадратично). Это потребует добавления все большего числа секунд координации к Всемирному координированному времени (UTC), поскольку UTC должно поддерживаться с точностью в одну секунду относительно равномерной шкалы UT1. (Секунда СИ, используемая сейчас для UTC, уже в момент принятия была немного короче, чем текущее значение секунды среднего солнечного времени.^[7]) Физически нулевой меридиан для Универсального времени оказывается почти всегда восточнее меридиана Земного времени как в прошлом, так и в будущем. +16800 с или 4⅔ часа соответствуют to 70° в.д. Это означает, что в −500 году вследствие более быстрого вращения Земли солнечное затмение происходило на 70° восточнее положения, которое следует из расчетов с использованием равномерного времени TT.

Все значения ΔT до 1955 года зависят от наблюдений Луны, связанных либо с затмениями либо с покрытиями. Сохранение углового момента в Системе Земля-Луна требует, чтобы уменьшение углового момента Земли вследствие приливного трения передавался Луне, увеличивая её угловой момент, что означает, что её расстояние до Земли должно увеличиваться, что, в свою очередь, вследствие третьего закона Кеплера приводит к замедлению обращения Луны вокруг Земли. Приведенные выше значения ΔT предполагают, что ускорение Луны, связанное с этим эффектом составляет величину dn/dt = −26″/век², где n — средняя угловая сидерическая скорость Луны. Это близко к лучшим экспериментальным оценкам для dn/dt, полученным в 2002 году: −25,858±0,003″/век²^[8], и поэтому оценки ΔT, полученные ранее исходя из значения −26″/век², принимая во внимание неопределенности и эффекты сглаживания в экспериментальных наблюдениях, можно не пересчитывать. В наше время UT определяется по измерению ориентации Земли по отношению к инерциальной системе отсчета, связанной с внегалактическими радиоисточниками, с поправкой на принятое соотношение между сидерическим и солнечным временем. Эти измерения, проводимые в нескольких обсерваториях, координируются Международной службой вращения Земли (IERS).

Величины дельта Т

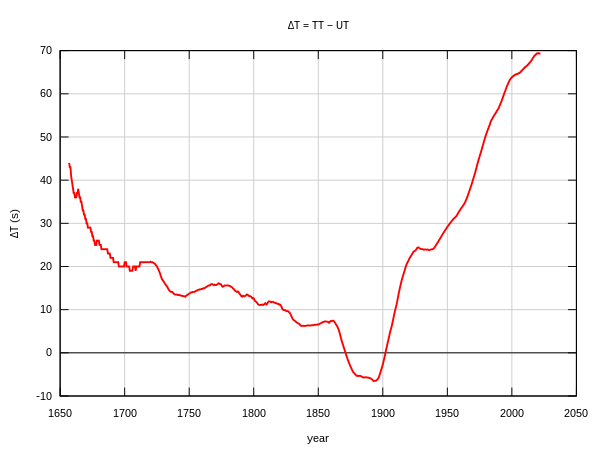ΔT на протяжении 1657—1984 гг.^[9]

Для 1900—1995 годов значения приведены согласно «Астрономия на персональном компьютере», четвёртое издание, 2002 год, Монтенбрук О., Пфеглер Т., для 2000 года — из английской Вики.

Год	дельта Т
1900	-2,72
1905	3,86
1910	10,46
1915	17,20
1920	21,16
1925	23,62
1930	24,02
1935	23,93
1940	24,33
1945	26,77
1950	29,15
1955	31,07
1960	33,15
1965	35,73
1970	40,18
1975	45,48
1980	50,54
1985	54,34
1990	56,86
1995	60,82
2000	63,83
2005	64,69
2010	66,07

Вычисление дельта Т

Приближенная формула для вычисления дельта Т

С 1972 года по наше время ΔT можно рассчитать зная количество секунд координации по формуле:

ΔT≃32,184+10+N,{\displaystyle \Delta T\simeq 32{,}184+10+N,}

где
32,184 секунд — разница между TT и TAI,
10 секунд — разница между TAI и UTC на начало 1972 года,
N — количество введенных с 1972 года секунд координации.

Формула дает погрешность не более 0,9 секунд. Например, на начало 1995 года было введено 19 секунд координации и формула дает ΔT=61,184 секунд, что лишь на 0,364 секунды превышает табличное значение.

Точная формула для вычисления дельта Т

Из бюллетеня А (Bulletin — A) Службы вращения земли IERS можно узнать разность между TAI и UTC (зависит от количества секунд координации, величина меняется редко) и между UT1 и UTC (величина постоянно меняется, в бюллетене даётся на полночь ежесуточно), тогда дельта Т можно вычислить точно по формуле:

ΔT=32.184s+(TAI−UTC)−(UT1−UTC).{\displaystyle \Delta T=32.184s+(TAI-UTC)-(UT1-UTC).}

Приблизительная формула вычисления дельта Т на будущее

Рассчитать дельта Т на будущее можно только приблизительно, ввиду того, что изменение вращения Земли недостаточно изучено. Тем не менее для расчёта, например, пути прохождения тени от солнечного затмения или времени покрытия звёзд Луной делать хотя бы приблизительный расчёт необходимо. Фред Эспеньяк (англ.)русск. при расчёте солнечных затмений на период 2005—2050 годов пользовался формулой^[10]

ΔT=62,92+0,32217⋅(y−2000)+0,005589⋅(y−2000)2,{\displaystyle \Delta T=62,92+0,32217\cdot \left(y-2000\right)+0,005589\cdot \left(y-2000\right)^{2},}

где y — год, для которого определяется дельта Т.

См. также

Приливное ускорение

Примечания

1. ↑ McCarthy & Seidelmann 2009, 88-89
2. ↑ Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, Nautical Almanac Offices of UK and USA (1961), at pp.9 and 71.
3. ↑ См. предложение Г. М. Клеменса в его статье G. M. Clemence «On the System of Astronomical Constants», Astronomical Journal v.53 (1948), #1170, 169—179; а также G. M. Clemence, «The Concept of Ephemeris Time», Journal for the History of Astronomy v.2 (1971), 73-79 (рассказывает об истории принятия предложения эфемеридного времени).
4. ↑ См. Newcomb’s Tables of the Sun (Washington, 1895), Введение и Раздел I. Основания таблиц, c.9 и 20, ссылаются на единицы времени относительно среднего полудня по Гринвичу, по среднему времени по Гринвичу, в единицах средних солнечных суток: и W de Sitter, on p.38 of Bulletin of the Astronomical Institutes of the Netherlands, v4 (1927), pp.21-38, «On the secular accelerations and the fluctuations of the moon, the sun, Mercury and Venus», где «астрономическое время, задается вращением Земли и используется во всех практических астрономических расчетах», и подчеркивается, что оно «отличается от ‘однородного’ или ‘ньютоновского’ времени».
5. ↑ См. с. 612 в Explanatory Supplement to the Astronomical Almanac, ed. P K Seidelmann, 1992, где подтверждается использование ET в эфемеридах Альманаха, начиная с 1960 г. издания.
6. ↑ См. F. R. Stephenson (1997), и Stephenson & Morrison (1995), а также другие цитируемые ниже публикации.
7. ↑ :(1)»The Physical Basis of the Leap Second», by D D McCarthy, C Hackman and R A Nelson, Astronomical Journal, vol.136 (2008), 1906—1908: «the SI second is equivalent to an older measure of the second of UT1, which was too small to start with and further, as the duration of the UT1 second increases, the discrepancy widens.»: (2) В конце 1950-х стал использоваться цезиевый стандарт, как для определения текущего значения секунды среднего солнечного времени (9192631830 периодов), так и для определения секунды эфемеридной шкалы (ET) (9192631770 +/-20 периодов), см. «Time Scales», by L. Essen, in Metrologia, vol.4 (1968), pp.161-165, on p.162. Для стандарта секунды СИ было выбрано значение 9192631770 периодов.
8. ↑ J.Chapront, M.Chapront-Touzé, G.Francou (2002): «A new determination of lunar orbital parameters, precession constant, and tidal acceleration from LLR measurements» (also in PDF). Astronomy & Astrophysics 387, 700—709
9. ↑ IERS Rapid Service/Prediction Center (c. 1986). Historic Delta T and LOD. Source attributed data to McCarthy and Babcock (1986) . Retrieved December 2009.
10. ↑ Fred Espenak, Jan Meeus: Polynomial Expressions for Delta T (ΔT)

• Stephenson, F. R. & Morrison, L.V. «Long-term fluctuations in the Earth’s rotation: 700 BC to AD 1990». Philosophical Transactions of the Royal Society of London, Series A 351 (1995) 165—202. JSTOR link. Includes evidence that the ‘growth’ in Delta-T is being modified by an oscillation with a wavelength around 1500 years; if that is true, then during the next few centuries Delta-T values will increase more slowly than is envisaged.

Ссылки

Дельта T — Википедия. Что такое Дельта T

ΔT (дельта T, Delta T, delta-T, deltaT, или DT) — разница между земным временем (TT) и всемирным временем (UT).

Тонкости определения

В литературе, выпущенной в разное время, могут встречаться немного отличающиеся определения ΔT (в зависимости от того, какая шкала равномерного времени была рекомендована для использования в астрономических расчетах в тот или иной период):

• ΔT=ET−UT (до 1984 года)
• ΔT=TDT−UT (с 1984 по 2001 годы)
• ΔT=TT−UT(с 2001 года по настоящее время).

Кроме того, под «Всемирным временем» может подразумеваться одна из его версий (UT0, UT1 и т. д.). Поэтому в специализированной литературе принято указывать, что имеется в виду под ΔT, например «DTD — UT1», что означает «Динамическое земное время минус Всемирное время версии UT1».

Несмотря на некоторые изменения в определении, физический смысл ΔT не меняется — это разница между идеальным равномерно текущим временем и «временем», определённым по вращению Земли (которое замедляется, причём неравномерно).

О неравномерности вращения Земли вокруг своей оси

Всемирное время (UT) является шкалой времени, основанной на суточном вращении Земли, которое не вполне равномерно на относительно коротких интервалах времени (от дней до столетий), и поэтому любые измерения времени, основанные на такой шкале, не могут иметь точность лучше чем 1 : 10⁸. Однако основной эффект проявляется на больших временах: на масштабах столетий приливное трение постепенно замедляет скорость вращения Земли примерно на 2,3 мс/сутки/век. Однако есть и другие причины, изменяющие скорость вращения Земли. Самой важной из них являются последствия таяния материкового ледникового щита в конце последнего ледникового периода. Это привело к уменьшению мощной нагрузки на земную кору и послеледниковой релаксации, сопровождающейся распрямлением и поднятием коры в приполярных областях — процесс, который продолжается и сейчас и будет продолжаться пока не будет достигнуто изостатическое равновесие. Этот эффект послеледниковой релаксации приводит к перемещению масс ближе к оси вращения Земли, что заставляет её вращаться быстрее (закон сохранения углового момента). Полученное из этой модели ускорение составляет около −0,6 мс/сутки/век. Таким образом, полное ускорение (на самом деле замедление) вращения Земли, или изменение длины средних солнечных суток составляет +1,7 мс/сутки/век. Эта величина хорошо соответствует среднему темпу замедления вращения Земли за последние 27 столетий.^[1]

Земное время (TT) является теоретически равномерной временной шкалой, определенной так, чтобы сохранить непрерывность с предшествующей равномерной шкалой эфемеридного времени (ET). ET основана на независимой от вращения Земли физической величине, предложенной (и принятой к применению) в 1948-52^[2] с намерением получить настолько однородную и не зависящую от гравитационных эффектов временную шкалу, насколько это возможно было в то время. Определение ET опиралось на солнечные таблицы (англ.)русск. Саймона Ньюкома (1895), интерпретированные новым образом, чтобы учесть определенные расхождения в наблюдениях.^[3]

Таблицы Ньюкома служили основой для всех астрономических солнечных эфемерид с 1900 по 1983 год. Изначально они были выражены (и в таком виде опубликованы) в терминах среднего времени по Гринвичу и средних солнечных суток,^[4] однако позднее, в особенности в отношении периода с 1960 по 1983 г., они трактовались как выраженные в рамках ET,^[5] в соответствии с принятым в 1948-52 предложением о переходе к ET. В свою очередь, ET могло теперь рассматриваться в свете новых результатов^[6] как шкала времени максимально близкая к среднему солнечному времени на интервале 1750 и 1890 (с серединой около 1820 года), поскольку именно в этом интервале проводились наблюдения, на основании которых были составлены таблицы Ньюкома. Хотя шкала TT является строго однородной (основана на единице секунды СИ, и каждая секунда строго равна каждой другой секунде), на практике она реализуется как Международное атомное время (TAI) с точностью около 1 : 10¹⁴.

Определение дельта Т из наблюдений

Время, определяемое положением Земли (точнее, ориентацией Гринвичского меридиана относительно фиктивного среднего Солнца), является интегралом от скорости вращения. При интегрировании с учётом изменения длины суток на +1,7 мс/сутки/век и выборе начальной точки в 1820 году (примерная середина интервала наблюдений, использованных Ньюкомом для определения длины суток), для ΔT получается в первом приближении парабола 31×((Год − 1820)/100)² в секунд. Сглаженные данные, полученные на основе анализа исторических данных о наблюдениях полных солнечных затмений дают значения ΔT около +16800 с в −500 году, +10600 с в 0, +5700 с в 500, +1600 с в 1000 и +180 с в 1500. Для времени после изобретения телескопа ΔT определяются из наблюдений покрытий звезд Луной, что позволяет получить более точные и более частые значения величины. Поправка ΔT продолжала уменьшаться после 16 века, пока не достигла плато +11±6 с между 1680 и 1866 года. В течение трех десятилетий до 1902 она оставалась отрицательной с минимумом −6,64 с, затем начала увеличиваться до +63,83 с в 2000 году. В будущем ΔT будет увеличиваться с нарастающей скоростью (квадратично). Это потребует добавления все большего числа секунд координации к Всемирному координированному времени (UTC), поскольку UTC должно поддерживаться с точностью в одну секунду относительно равномерной шкалы UT1. (Секунда СИ, используемая сейчас для UTC, уже в момент принятия была немного короче, чем текущее значение секунды среднего солнечного времени.^[7]) Физически нулевой меридиан для Универсального времени оказывается почти всегда восточнее меридиана Земного времени как в прошлом, так и в будущем. +16800 с или 4⅔ часа соответствуют to 70° в.д. Это означает, что в −500 году вследствие более быстрого вращения Земли солнечное затмение происходило на 70° восточнее положения, которое следует из расчетов с использованием равномерного времени TT.

Все значения ΔT до 1955 года зависят от наблюдений Луны, связанных либо с затмениями либо с покрытиями. Сохранение углового момента в Системе Земля-Луна требует, чтобы уменьшение углового момента Земли вследствие приливного трения передавался Луне, увеличивая её угловой момент, что означает, что её расстояние до Земли должно увеличиваться, что, в свою очередь, вследствие третьего закона Кеплера приводит к замедлению обращения Луны вокруг Земли. Приведенные выше значения ΔT предполагают, что ускорение Луны, связанное с этим эффектом составляет величину dn/dt = −26″/век², где n — средняя угловая сидерическая скорость Луны. Это близко к лучшим экспериментальным оценкам для dn/dt, полученным в 2002 году: −25,858±0,003″/век²^[8], и поэтому оценки ΔT, полученные ранее исходя из значения −26″/век², принимая во внимание неопределенности и эффекты сглаживания в экспериментальных наблюдениях, можно не пересчитывать. В наше время UT определяется по измерению ориентации Земли по отношению к инерциальной системе отсчета, связанной с внегалактическими радиоисточниками, с поправкой на принятое соотношение между сидерическим и солнечным временем. Эти измерения, проводимые в нескольких обсерваториях, координируются Международной службой вращения Земли (IERS).

Величины дельта Т

ΔT на протяжении 1657—1984 гг.^[9]

Для 1900—1995 годов значения приведены согласно «Астрономия на персональном компьютере», четвёртое издание, 2002 год, Монтенбрук О., Пфеглер Т., для 2000 года — из английской Вики.

Год	дельта Т
1900	-2,72
1905	3,86
1910	10,46
1915	17,20
1920	21,16
1925	23,62
1930	24,02
1935	23,93
1940	24,33
1945	26,77
1950	29,15
1955	31,07
1960	33,15
1965	35,73
1970	40,18
1975	45,48
1980	50,54
1985	54,34
1990	56,86
1995	60,82
2000	63,83
2005	64,69
2010	66,07

Вычисление дельта Т

Приближенная формула для вычисления дельта Т

С 1972 года по наше время ΔT можно рассчитать зная количество секунд координации по формуле:

ΔT≃32,184+10+N,{\displaystyle \Delta T\simeq 32{,}184+10+N,}

где
32,184 секунд — разница между TT и TAI,
10 секунд — разница между TAI и UTC на начало 1972 года,
N — количество введенных с 1972 года секунд координации.

Формула дает погрешность не более 0,9 секунд. Например, на начало 1995 года было введено 19 секунд координации и формула дает ΔT=61,184 секунд, что лишь на 0,364 секунды превышает табличное значение.

Точная формула для вычисления дельта Т

Из бюллетеня А (Bulletin — A) Службы вращения земли IERS можно узнать разность между TAI и UTC (зависит от количества секунд координации, величина меняется редко) и между UT1 и UTC (величина постоянно меняется, в бюллетене даётся на полночь ежесуточно), тогда дельта Т можно вычислить точно по формуле:

ΔT=32.184s+(TAI−UTC)−(UT1−UTC).{\displaystyle \Delta T=32.184s+(TAI-UTC)-(UT1-UTC).}

Приблизительная формула вычисления дельта Т на будущее

Рассчитать дельта Т на будущее можно только приблизительно, ввиду того, что изменение вращения Земли недостаточно изучено. Тем не менее для расчёта, например, пути прохождения тени от солнечного затмения или времени покрытия звёзд Луной делать хотя бы приблизительный расчёт необходимо. Фред Эспеньяк (англ.)русск. при расчёте солнечных затмений на период 2005—2050 годов пользовался формулой^[10]

ΔT=62,92+0,32217⋅(y−2000)+0,005589⋅(y−2000)2,{\displaystyle \Delta T=62,92+0,32217\cdot \left(y-2000\right)+0,005589\cdot \left(y-2000\right)^{2},}

где y — год, для которого определяется дельта Т.

См. также

Приливное ускорение

Примечания

1. ↑ McCarthy & Seidelmann 2009, 88-89
2. ↑ Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, Nautical Almanac Offices of UK and USA (1961), at pp.9 and 71.
3. ↑ См. предложение Г. М. Клеменса в его статье G. M. Clemence «On the System of Astronomical Constants», Astronomical Journal v.53 (1948), #1170, 169—179; а также G. M. Clemence, «The Concept of Ephemeris Time», Journal for the History of Astronomy v.2 (1971), 73-79 (рассказывает об истории принятия предложения эфемеридного времени).
4. ↑ См. Newcomb’s Tables of the Sun (Washington, 1895), Введение и Раздел I. Основания таблиц, c.9 и 20, ссылаются на единицы времени относительно среднего полудня по Гринвичу, по среднему времени по Гринвичу, в единицах средних солнечных суток: и W de Sitter, on p.38 of Bulletin of the Astronomical Institutes of the Netherlands, v4 (1927), pp.21-38, «On the secular accelerations and the fluctuations of the moon, the sun, Mercury and Venus», где «астрономическое время, задается вращением Земли и используется во всех практических астрономических расчетах», и подчеркивается, что оно «отличается от ‘однородного’ или ‘ньютоновского’ времени».
5. ↑ См. с. 612 в Explanatory Supplement to the Astronomical Almanac, ed. P K Seidelmann, 1992, где подтверждается использование ET в эфемеридах Альманаха, начиная с 1960 г. издания.
6. ↑ См. F. R. Stephenson (1997), и Stephenson & Morrison (1995), а также другие цитируемые ниже публикации.
7. ↑ :(1)»The Physical Basis of the Leap Second», by D D McCarthy, C Hackman and R A Nelson, Astronomical Journal, vol.136 (2008), 1906—1908: «the SI second is equivalent to an older measure of the second of UT1, which was too small to start with and further, as the duration of the UT1 second increases, the discrepancy widens.»: (2) В конце 1950-х стал использоваться цезиевый стандарт, как для определения текущего значения секунды среднего солнечного времени (9192631830 периодов), так и для определения секунды эфемеридной шкалы (ET) (9192631770 +/-20 периодов), см. «Time Scales», by L. Essen, in Metrologia, vol.4 (1968), pp.161-165, on p.162. Для стандарта секунды СИ было выбрано значение 9192631770 периодов.
8. ↑ J.Chapront, M.Chapront-Touzé, G.Francou (2002): «A new determination of lunar orbital parameters, precession constant, and tidal acceleration from LLR measurements» (also in PDF). Astronomy & Astrophysics 387, 700—709
9. ↑ IERS Rapid Service/Prediction Center (c. 1986). Historic Delta T and LOD. Source attributed data to McCarthy and Babcock (1986) . Retrieved December 2009.
10. ↑ Fred Espenak, Jan Meeus: Polynomial Expressions for Delta T (ΔT)

• Stephenson, F. R. & Morrison, L.V. «Long-term fluctuations in the Earth’s rotation: 700 BC to AD 1990». Philosophical Transactions of the Royal Society of London, Series A 351 (1995) 165—202. JSTOR link. Includes evidence that the ‘growth’ in Delta-T is being modified by an oscillation with a wavelength around 1500 years; if that is true, then during the next few centuries Delta-T values will increase more slowly than is envisaged.

Ссылки

Тепловой расчёт и подбор количества отопительных приборов

После выполнения расчёта теплопотерь здания для проектирования отопления становится известно сколько тепла теряет здание. Необходимо подобрать отопительные приборы. Отопительные приборы бывают разные (Типы отопительных приборов). Тут всё зависит от множества факторов: Параметры системы отопления, дизайном или просто имеющимся уже в наличии приборам.

Понятно, что чем больше батарея, тем больше тепла она передаст помещению. Но примерно одинаковые по размеру конвектор и радиатор отдают разное количество тепла.

Как правильно подобрать отопительный прибор в помещение?

Например: Коттедж, спальная комната на 2 этаже с двумя окнами и теплопотерями 2680 Вт.(Теплопотери дома)

.

Отопительные приборы выбрали: Алюминиевые радиаторы водяного отопления Elegance 500.

.

Необходимо установить 2 батарее по X секций. Одну батарею под каждое окно.

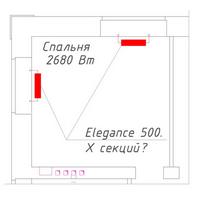
Кажется, что вроде ничего сложного. На всех сайтах и в паспорте производителя указано, что теплоотдача одной секции радиатора Elegance 500 — 190 Вт.

Теплопотери помещения делим на теплоотдачу одной секции: 2680/190 = 14,1. Т.е. надо поставить по 7 секций под каждое окно. Да и с житейской точки зрения тоже вроде нормально.

Но этот подсчёт НЕВЕРНЫЙ!

Открываем Технический паспорт радиаторов Elegance: Скачать с облака.Mail.ru ¹⁸³ и смотрим таблицу в разделе 3.

Теплотехнические характеристики секции при (дельта)Т = 70ºС модель El.500 — теплоотдача 190 Вт.

А что такое (дельта)Т — Это разница между средней температурой воды в радиаторе и температурой в помещении.

Даже сам производитель в паспорте в п.3.4 приводит формулу для расчёта теплоотдачи одной секции.

Посчитаем теплоотдачу по этой формуле:

190 Вт — Теплоотдача одной секции при (дельта)Т 70;

(80+60)/2-20 — средняя температура воды в радиаторе минус температура в комнате

Q = 190 Вт*((((80+60)/2)-20)/70)^1.33 = 121 Вт.

И получается, что при (дельта)Т 50 теплоотдача одной секции всего 121 Вт, против 190. И в помещении спальни необходимо установить не 14 секций, а 2680/121=22 секции. По 11 под каждое окно. Или 10 и 12.

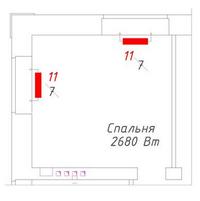
При подборе отопительного прибора не надо верить рекламным буклетам, всегда необходимо открыть паспорт прибора и посмотреть.

Совет: после расчёта необходимого количества секций, добавьте 1-2 секции. Если будет жарко, то всегда можно убавить теплоотдачу регулятором. А вот прибавить в сильные холода уже не получиться.

Как рассчитать радиаторы отопления.

Как рассчитать радиаторы отопления.

Зима, мороз наряжает стёкла окон резными узорами… Да, так было когда-то. Сейчас уже редко где встретишь такое явление. Прогресс движется вперёд, люди придумывают что-то новое для создания удобства и уютной атмосферы в доме.В данном случае я говорю о герметичных стеклопакетах.

Но о каком уюте может идти речь когда в доме холодно и по утрам так не хочется вылазить из-под тёплого одеяла? Картинка не из приятных. В этой статье я расскажу как правильно рассчитать количество секций радиатора, необходимое для отопления комнаты, чтобы не приходилось мёрзнуть от недостатка тепла зимними вечерами.

Кто-то, как мне довелось увидеть однажды, производит расчет деля мощность радиатора на квадратные метры комнаты — это в корне неправильно! Нужно считать исходя из количества кубических метров! Высота потолков в разных домах может быть разной. Как правило от 2,5 до 3м. И это не предел, ведь кому-то, например, нравятся высокие потолки.

Без лишней теории просто и доступно.

Итак, мы считаем:
длина — 5м,
ширина комнаты — 3м,
высота — 2,5м
соответственно объём прогреваемого воздуха можно найти перемножив эти величины: 5*3*2,5=37,5м3

Радиатор, который подойдёт нам по высоте, то есть разместится под подоконником, — тот, у которого высота 500мм.(у вас может быть и меньше). В документации написано, что одна секция такого радиатора выдаёт 145 Вт при дельте Т=70 С.

145 Вт достаточно, чтобы отапливать 3,6 м3 помещения. У нас 37,5 м3. Мы делим общий объем — 37,5 м3 на 3,6 м3 и получаем количество секций, необходимых нам.

37,5/3,6=10,417
Округляем, получаем 10 секций радиатора на комнату.

Если окон 2, возьмем два радиатора по 6 секций, (если два окна, то скорее всего у вас это угловая комната и тепла потребуется больше) если окно одно — один радиатор на 10 секций.

Что значит «дельта Т»?

В физике так принято обозначать разницу каких-либо величин, в данном случае — разница температур.

dT=(T1+T2):2-T3
Где dT — дельта Т, T1 — температура подачи, T2 — температура обратки, T3 — температура помещения.

dT = (95 + 85) : 2 — 20 = 70°

То есть температура теплоносителя (воды) на входе в радиатор 95° плюс температура теплоносителя (остывшей воды) на выходе из радиатора 85°, полученный результат делим на 2 и вычитаем температуру помещения — 20°.

На практике такое, конечно, нереально. Никто не ждет пока вода в радиаторе остынет ровно на 15°. Происходит постянная циркуляция. То есть дельта T для радиатора весьма условная единица и в нашем случае она нужна лишь для сравнения характеристик разных моделей радиаторов.

Есть ещё один важный момент! Если ваша комната угловая или под вами подвал, либо над вами крыша, увеличивайте необходимое количество тепловой энергии на коэффициент 1,1 — 1,3. Лично я считаю, что лучше поставить дополнительно одну секцию радиатора. Переизбыток тепла легко регулируется терморегулятором или обычным шаровым краном, а вот его недостаток восполнить проблематично.

Итог:
1 секция радиатора мощностью 145 Вт способна отапливать 3,6м3.
На 1 метр кубический уходит 40 ватт мощности!
Если комната угловая, то на 1 метр кубический нужно уже 44 — 52Вт
Вот и вся арифметика!

Формула дельта

La формула дельта стабилизация, что и дельта разнородного состояния второго градуса, оттиене далла дифференциального траектория квадратов-дельта-терминов первого градуса и квадрупольного продоттраильского коэффициента вторичного градиента il termine noto.

Molto più semplice da esprimere coi simboli che a parole. В целом, как правило, это уравнение второго градуса

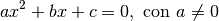
la формула для расчета дельты è la seguente

Come potete osservare è il coefficiente del termine di Primo Grado, di Cucoli ,Va poi sottratto il quadruplo del prodotto tra che sono, rispettivamente, il coefficiente del termine di secondo grado e il termine noto.

Допускается, что дельта, это студия дель только может предоставить информацию о номере и на типе решений, которые имеют одно градусное уравнение, для каждой расчетной точки. Nello specifico:

— se l’equazione ha due soluzioni reali e diffte;

— se l’equazione ammette due radici reali duplicidenti;

— se l’equazione non è risolvibile nell’insieme R dei numeri reali, ma ammette due radici complesse e coniugate.

Indicando con le due soluzioni di un’equazione di secondo grado, в каждом из трех случаев, когда применяется формула, соответствующая переходу

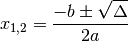
Esempi di application della formula delta

Для использования формулы vista poc’anzi

dove, al posto di vanno sostituiti, rispettivamente, i numeri 7, -9 e 2.

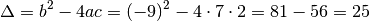
Poich un numeri больше нуля, l’equazione данные доступны благодаря реальным решениям.

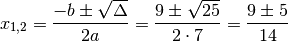
Ossia

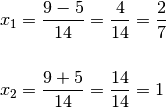
2)

Формула дельта состоит из

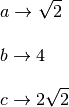
Avendo chiaro come si svolge2000

или 971 9000 проданных радикалов per cui l’equazione ha due radici reali совпадение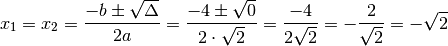

Nell’ultimo passaggio abbiamo effettuato una semplice razionalizzazione.

3)

Nell’equazione data, pertanto

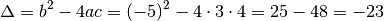
Il delta è negativo, quindi l’equazione non ha radici reali.

Formula delta Quarti

Se in’equazione di secondo grado il coefficiente del termine di primo grado è un multiplo di 2, invece della formula del delta si può usare la formula del delta quti.

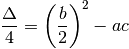
Сценарии использования формулы дельта кварт, решения для воды с датой

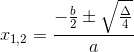
Дельта квартал имеет отдельную форму семпликации кальколи; Вычисление дельты или дельты кварталов (возможно) и все без исключения: информация о том, что такое дедуктивное выражение в этом звуке, и идентичны звуковым решениям.

Пример применения формулы дельта кварт

Пошешь коэффициент терминов при первом градусе и угле 2, который является мультипло ди 2, возможно использование формулы дельта кварт

quindi due radici reali e Difference, date da

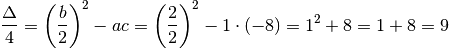
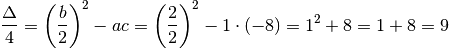
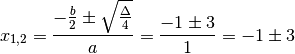
Di consguenza

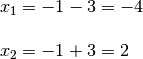
Lasciamo a voi il compito di application la formula delta e verificare, which si ottengono le stesse soluzioni.;)

***

Con questo è tutto! Per memorizzare la formula del delta vi consigliamo di fare molti esercizi, e a tal proposito potete fare uso della nostra scheda di esercizi sulle equazioni di secondo grado.

Se invece volete sapere come si ricava la formula del delta rimandiamo alla nostra pagina sulla formula del discinante.

.

Дельта-геометрия — RepRap

Введение

Дельта-робот или принтер — это робот, платформа которого поддерживается тремя парами рук, расположенными в треугольнике. Пары параллельных рычагов поддерживают горизонтальность платформы, и движение этих рычагов перемещает платформу в трех измерениях. Существует множество решений, но некоторые из них используются практически.

Есть два принципа смещения пар рычагов:

• Каждая пара рычагов установлена ​​на основном шарнирном рычаге, движение создается за счет вращения этого основного рычага.Геометрия — это дельта вращения или «дельта Клавеля» по имени ее изобретателя. Этот принцип широко используется в машинах «подобрать и разместить» в самых разных отраслях промышленности, от электронной до пищевой. Эту систему можно найти в Delta от Energetic или на принтерах FirePick Delta.

• Пары рычагов прикреплены к каретке, скользящей по параллельным рельсам. Эта геометрия называется линейной дельтой и является наиболее частым типом, используемым в мире 3D-принтеров, машины, вызывающие движение, — это Росток и Коссель.Термин «параллельная дельта» не должен использоваться, поскольку все роботы с параллельными руками называются параллельными роботами.

Есть еще одно решение без жесткой механики — подвесить платформу на тросах. Есть несколько примеров, и особенно Skydelta или эта подвесная дельта.

Кинематический расчет линейной дельты прост, потому что каретка движется по прямой линии, поэтому горизонтальное движение платформы связано с вертикальным перемещением каретки по теореме Пифагора (которая утверждает, что квадрат длины диагонали равен сумме сторон треугольников в квадрате, треугольник должен быть прямоугольным).Здесь диагональ — это длина руки, постоянная, вертикальная ветвь — это относительное вертикальное положение платформы и каретки, горизонтальная ветвь — это относительное горизонтальное положение платформы и каретки.

Вычислить нетрудно, но для принтера нужно много вычислять квадратные корни. Платы управления на базе 8-битных процессоров с трудом справляются с этими вычислениями, поэтому для этих процессоров было выполнено много тонкой оптимизации программного обеспечения для дельта-геометрии. 32-битные контроллеры становятся предпочтительными платами контроллеров для дельта-принтеров, поскольку они имеют гораздо более быстрые процессоры и совсем не борются с математикой.Следует отметить, что три столбца ползунков могут быть расположены в неравностороннем треугольнике, и были протестированы асимметричные положения, в частности, дельта «квадрат» с углами 90 °, 90 ° и 180 °.

Геометрия линейного дельты

Схемы

Угол рычага с эффектором в центре является результатом длины плеч, минимального угла и углов плеч при максимальном диаметре. Для минимального угла 20 ° этот угол составляет около 60 ° для вертикалей рычага максимального диаметра, но если минимальный угол увеличить, он может быть больше.Минимальные углы 22 ° дают угол 63 ° с вертикальными рычагами.

Рычаги могут не достигать вертикали из-за проблемы с зазором, в частности, с частями охлаждающих вентиляторов или вспомогательными принадлежностями. В этом случае для данного минимального угла длина плеча может быть уменьшена, и угол, когда эффектор находится в центре, будет меньше.

С другой стороны, у некоторых принтеров есть рычаги, способные перемещаться по вертикали (например, Rostock Max).

Минимальный угол плеча при максимальном диаметре эффектора является одним из основных параметров конструкции.Это важно для стабильности, точности и скорости каретки. Небольшой угол вызывает высокую скорость каретки при заданной горизонтальной скорости исполнительного механизма. Низкий угол также снижает стабильность эффектора. Как правило, угол 20 ° рассматривается как практический минимум и обеспечивает скорость каретки в 2,75 раза выше, чем горизонтальная скорость эффектора. Некоторые принтеры с теоретическим минимальным углом 15 ° могут потерять ступеньки при максимальном диаметре.

Коэффициент ускорения для заданного угла рычага

мини-угол	множитель скорости
22.5 °	2,41
20 °	2,75
17,5 °	3,17
15 °	3,73
12,5 °	4,51

,Обзор подключения трансформатора треугольник

Обзор подключения трансформатора треугольник (на фото: паспортная табличка трансформатора КВАДРАТНЫЙ)

Соединение треугольник-треугольник

В этом типе подключения как трехфазная первичная, так и вторичная обмотки соединены треугольником, как показано на Рисунок 1 :

Рисунок 1 — Подключение трансформатора треугольник-треугольник

Напряжения на первичной и вторичной сторонах могут быть показаны на векторной диаграмме ( Рисунок 2 ):

Рисунок 2 — Диаграмма соединения трансформатора треугольник-треугольник

Это соединение оказалось экономичным для больших трансформаторов низкого напряжения, поскольку оно увеличивает количество витков на фазу.

Ключевые моменты

1. Первичная сторона Линейное напряжение = Линейное напряжение вторичной стороны .
2. Первичная сторона Фазное напряжение = Фазное напряжение вторичной стороны .
3. Нет сдвига фаз между первичным и вторичным напряжениями.

Преимущества подключения трансформатора треугольник-треугольник

Синусоидальное напряжение на вторичной обмотке

Для того, чтобы вторичное напряжение было синусоидальным, ток намагничивания трансформатора должен содержать третью гармоническую составляющую.Соединение треугольником обеспечивает замкнутый путь для циркуляции третьей гармонической составляющей тока. Поток остается синусоидальным, что приводит к синусоидальным напряжениям.

Перенести 58% нагрузки, если одна передача неисправна в банке трансформаторов

Если имеется группа однофазных трансформаторов, подключенных по схеме треугольник-треугольник, и если один из трансформаторов отключен, то питание может быть продолжено с оставшимися двумя трансформаторами, конечно, с пониженным КПД.

Экономичный для низкого напряжения

Из-за соединения треугольником фазное напряжение совпадает с линейным напряжением, поэтому обмотка имеет большее количество витков.Но фазный ток в (1 / √3) раз больше линейного тока. Следовательно, сечение обмоток очень меньше. Это делает подключение трансформаторов низкого напряжения экономичным.

Отсутствие третьей гармоники напряжения

Из-за замкнутого треугольника напряжения третьей гармоники отсутствуют. Отсутствие звезды или нейтральной точки в некоторых случаях оказывается преимуществом.

Недостатки подключения трансформатора треугольник-треугольник

Из-за отсутствия нейтральной точки не подходит для трехфазной четырехпроводной системы.Требуется дополнительная изоляция, и напряжение, возникающее между обмоткой и сердечником, будет равно полному линейному напряжению в случае замыкания на землю на одной фазе.

Приложение

1. Подходит для больших трансформаторов низкого напряжения.
2. Этот тип подключения обычно необычен, но используется на некоторых промышленных объектах для уменьшения воздействия сбоев SLG на первичную систему.
3. Он обычно используется в системах, где необходимо проводить большие токи при низком напряжении, и особенно когда необходимо поддерживать непрерывность работы, даже если на одной из фаз возникает неисправность.

.