| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты. Поделиться:
| |||||||||||||||||||||||||||||||||
| Развернуть структуру обучения | Свернуть структуру обучения |
| Определение хордыХорда — это отрезок, который соединяет две точки заданной кривой.  Хорда может быть у дуги, окружности, эллипса и т.д. Хорда может быть у дуги, окружности, эллипса и т.д. Часть кривой, заключенной между двумя точками хорды, называется дугой. Плоская фигура, заключенная между дугой и ее хордой называется сегментом. Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности. Свойства хорды к окружности
Свойства хорды и вписанного углаНа рисунке [1] вписанный угол обозначен обозначен как ACB, хорда окружности — AB
Свойства хорды и центрального углаНа рисунке [2] центральный угол обозначен как AOB, хорда как AB.
Формулы нахождения хордыОбозначения в формулах: l — длина хорды α — величина центрального угла R — радиус окружности d — длина перпендикуляра, проведенного от центра окружности к хорде Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Решение задачПримечание.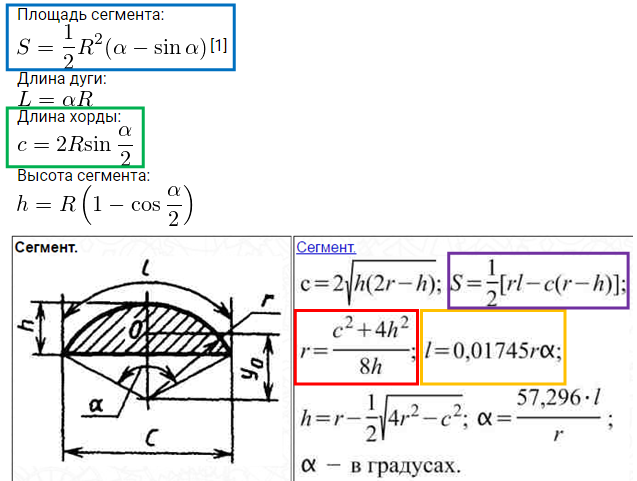 Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.Задача.
Решение. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 х2 = 10 x = √10 Откуда Ответ: 5√10 Задача.
Решение.  Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг). Поскольку градусная мера окружности равна 360 градусам, то 3,5х + 5,5х + 3х = 360 Откуда градусные величины центральных углов равны:
90 / 2 = 45 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;
|
Хорды — Длины — Таблицы
Длину хорд можно определить по таблице или по формуле [c. 40]
40]В третьей части таблицы приводят диаметр делительной окружности и толщину зуба (если отсутствуют данные для контроля) для косозубых колес — осевой шаг (а, или ход винтовой линии 5, или угол наклона зуба Ро на основном цилиндре для шевингуемых или шлифуемых колес, или при наличии в данных для контроля показателя Ьf — диаметр основной окружности и радиус кривизны в начале рабочего участка зуба (можно указать высоту кр рабочего участка зуба) толщину зуба по хорде или длину общей нормали — при отсутствии этих показателей во второй части сведения о сопряженном колесе и другие справочные данные. [c.35]
Круг радиуса, равного единице — Длина дуг, хорд, стрелок и площадь сегментов — Таблицы 37, 38 Круги шлифовальные — см. [c.754] Примечание. Радиус г для данной дуги I и стрелки Л определяется из отношения г=—, где /о —длина дуги, которая при радиусе 1 соответствует заданному —, ио-/(I я мещенному в графе 1 таблицы.
 Если г—радиус круга, а ср —центральный угол в градусах, то 1) длина хорды S = 2г sin
[c.95]
Если г—радиус круга, а ср —центральный угол в градусах, то 1) длина хорды S = 2г sin
[c.95]Характеристика логарифма 77 Характеристики вероятностные 326 Хорды — Длины — Таблицы 37 Храповые механизмы — см. Механизмы храповые [c.590]
ТАБЛИЦА VI. ЭЛЕМЕНТЫ КРУГА ДЛИНА ДУГИ, СТРЕЛКА, ДЛИНА ХОРДЫ И ПЛОЩАДЬ СЕГМЕНТА КРУГА ДЛЯ РАДИУСА у — — 1 [c.37]
Во второй части таблицы параметров венца приводят данные для контроля взаимного положения разноименных профилей зубьев по одному из следующих вариантов постоянная хорда зуба и высота до постоянной хорды длина общей нормали W толщина по хорде зуба и высота до хорды торцовый [c.472]
Для деления окружности на равное число частей пользуются таблицами хорд (табл. 95). Вычислив длину хорды для данного числа делений, откладывают полученную величину на разделяемой окружности. [c.193]
В таблице против числа делений 12 находим величину хорды, равную 0,5176. Умножив найденную длину хорды на радиус делимой окружности, находим длину хорды, стягивающей Vi2 часть окружности радиусом 100 мм.
[c.84]
Умножив найденную длину хорды на радиус делимой окружности, находим длину хорды, стягивающей Vi2 часть окружности радиусом 100 мм.
[c.84]
По таблице находят, что при 15 делениях, т. е. при центральном угле, равном 24°, длина хорды (5) для окружности радиуса, равного единице, есть 0,4158. [c.99]
Если при заданном подъеме (отношении стрелы к хорде) длина хорды равна а, то помещенное в таблице значение длины дуги должно быть умножено на а, а площадь сегмента — на а . [c.35]
Длину измеренной хорды отсчитывают непосредственно по нониусу 4. Определение номинальной толщины зуба и высоты до постоянной хорды производят по заранее составленным таблицам этих величин или расчетом по формулам, помещенным в справочниках для машиностроителей. [c.134]
Длина хорды, при помощи которой делят окружность на конгруэнтные дуги, зависит от числа делений и величины диаметра d окружности (берется из табл.
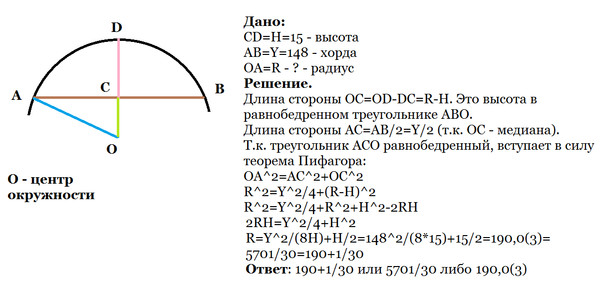 4). Например, для деления окружности диаметром 100 мм на девять конгруэнтных дуг в первой графе таблицы находим число делений 9. Во второй графе этому числу соответствует хорда длиной 0,34202 х й — 0,34202 х 100, что составляет приближенно 34,2 мм. При помощи циркуля или циркуля-измерителя этим размером засекают на окружности точки деления.
[c.47]
4). Например, для деления окружности диаметром 100 мм на девять конгруэнтных дуг в первой графе таблицы находим число делений 9. Во второй графе этому числу соответствует хорда длиной 0,34202 х й — 0,34202 х 100, что составляет приближенно 34,2 мм. При помощи циркуля или циркуля-измерителя этим размером засекают на окружности точки деления.
[c.47]Библиографические указания. Определению сил, действующих на тонкие тела, которые движутся в потоке жидкости или газа, посвящена обширная литература [4, 5, 12, 14, 15, 24, 27, 28, 31, 39, 43, 52, 67, 74]. Изложение этого вопроса применительно к задачам аэроупругости можно найти в книгах [4, 15, 39, 67]. Приближенные формулы для больших сверхзвуковых скоростей приведены в статьях [27, 31, 74] сопоставление этих формул дано в книге [15]. Области применения различных аэродинамических теорий приведены в табл. 1 [39]. В этой таблице к — приведенная частота по выражению (7) 6 — отношение толщины или амплитуды к хорде крыла 1, — удлинение (отношение длины крыла к хорде). [c.473]
[c.473]
Приборы для деления окружностей. Применение простейших приборов для деления окружностей на равные части и отыскания длин хорд, соответствующих заданным центральным углам, освобождает разметчиков от вспомогательных графических построений или расчетов с применением таблиц (см. стр. 51). [c.269]
Приборы для деления окружностей на равные части и определения хорд по центральным углам (фиг. 200) позволяют по заданному радиусу окружности без вычислений или таблиц определять длины хорд (стороны вписанных многоугольников), делящих окружности на любое число частей, а также определять хорды, соответствующие заданным центральным углам. [c.270]
Нанесение наклонных рисок. Наклонные линии под заданными углами могут быть нанесены тремя способами построением прямоугольного треугольника по его сторонам и углам построением угла наклона прямых по длине хорды, взятой из таблицы (см. стр. 37) при помощи специальных инструментов и приспособлений (см.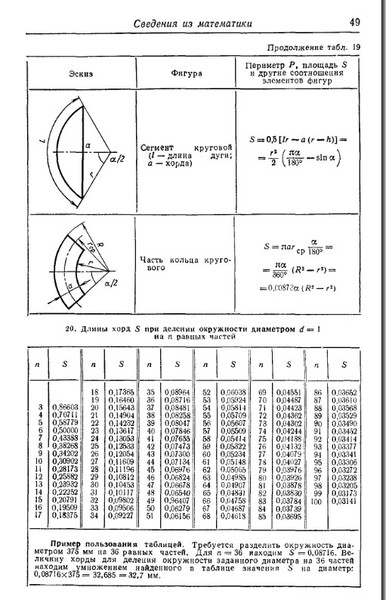 стр. 303).
[c.316]
стр. 303).
[c.316]
Деление окружности на неравные части производят при помощи таблиц [41, в которых длина хорды определяется по углу между соседними лучами. [c.147]
В случае недоступности вершины полного конуса построение развертки ведут иначе. Вначале по формула. определяют R, г и а, а затем по таблице 14] —длины хорд АБ п ВГ и стрелки hi и /ij. Последовательность построения дуги по размерам хорды и стрелки приведена в п. 53 (см. рис. 84, е). [c.152]
| Таблица 7. Длины дуг I, хорд а и стрелок й сегментов круга в зависимости от центрального угла а при г = |
 При делении окружности на равные части или при построении правильных многоугольников пользуются так называемой таблицей хорд, которая содержит ряд коэффициентов для определения длины стороны правильного многоугольника, вписанного в окружность данного диаметра.
[c.119]
При делении окружности на равные части или при построении правильных многоугольников пользуются так называемой таблицей хорд, которая содержит ряд коэффициентов для определения длины стороны правильного многоугольника, вписанного в окружность данного диаметра.
[c.119]При плоскостной разметке приходится выполнять разнообразные построения делить прямые линии на равные части, проводить перпендикулярные и параллельные линии, строить углы, делить углы и окружности на равные части и т. д. Указанные построения слесарь должен делать быстро и точно. Для деления окружности на равное число частей можно пользоваться таблицей хорд (табл. 7). Вычислив длину хорды для данного числа делений, откладывают полученную величину на разделяемой окружности. [c.49]
| Таблица 9.1 Стрелы круговых кривых в середине хорды длиной 20 м |
 [c.38]
[c.38]Хорды — Длина — Таблицы 131 [c.602]
Во второй части таблицы приводят данные для контроля взаимного положения разноименных профилей зубьев по одному из следующих вариантов 1) постоянная хорда зуба и высота до постоянной хорды /г 2) длина общей нормали 3) толщина по хорде зуба у и высота до хорды Тг 4) торцовый размер по роликам (шарикам) М и диаметр ролика (шарика) [c.288]
Если радиус/ не равен единице, то для определения длины дуги /, длины стрелки /) и длины хорды з нужно табличные значения умножить на R. Таблица 4 [c.23]
Эйлер указывает, что произведение длины полной кривой на ее хорду равно площади круга радиуса, равного горизонтальному прогибу. При взятых четырехзначных таблицах получается (а — отброшена) по формулам (40), (41) и (26) 2 1,8541 2 0,8471 и я=1,4142 что дает разницу на единицу в третьем знаке после запятой. [c.12]
ТАБЛИЦА КОЭФФИЦИЕНТОВ Кз, и Кь для ПОДСЧЕТА ДЛИН ДУГ /, СТРЕЛОК Л И ДЛИН ХОРД с в ЗАВИСИМОСТИ ОТ УГЛА а°
[c. 259]
259]
При фрезеровании зубчатых колес на фрезерном станке качество отфрезерованного зубчатого колеса можно определить не только измерением толщины зуба по постоянной хорде с помощью штангензубомера, но и путем измерения длины общей нормали (рис. 9) (длина общей нормали определяется по формулам или по специально подготовленным таблицам) [c.187]
Чтобы разде.шть окружность на любое число равных частей, проще всего пользоваться специальными таблицами (например, табл. 12 на стр. 23), в которых указана длина хорды х для окружности радиусом / =1. [c.154]
Примечание. Делительная толщина по хорде 51 — длина хорды, стягивающей дугу, по которой измеряется толщина зуба по делительной окружности. Делительная высота до хорды зуба ка — крат-чайщее расстояние от вершины зуба до средней точки делительной толщины по хорде. Для определения размеров вг и йо для модулей, отличных от т= . мм, необходимо данны е таблицы умножить на величину модуля. Например, при модуле 3 мм, числе зубьев 30 ка=ЗХ XI,0206 = 3,0618 3,06 мм = ЗХ 1,5700 = 4,71 мм.
[c.191]
Например, при модуле 3 мм, числе зубьев 30 ка=ЗХ XI,0206 = 3,0618 3,06 мм = ЗХ 1,5700 = 4,71 мм.
[c.191]
При заданных силе тяги, радиусе и концевой скорости несущего винта индуктивная и профильная мощности могут быть минимизированы соответствующим выбором крутки и сужения. На внешней части лопасти, где нагрузки самые большие, оптимальные распределения длин хорд и углов установки можно хорошо аппроксимировать линейными функциями. В самом деле, с лопастями, линейно закрученными на углы от —8 до 12°, получается почти весь тот выигрыш (по сравнению с незакру-ченными лопастями), который дают лопасти с идеальной круткой. Лопасти с линейной круткой просты в производстве, так что значительное улучшение аэродинамических характеристик достигается за счет лишь небольшого увеличения стоимости производства. Сужение также улучшает аэродинамические характеристики, но вследствие высокой стоимости производства оправдывается только для очень больших несущих винтов. В приведеной ниже таблице, составленной по данным Гессоу
[c. 79]
79]
Примечание. Нормальной точностью построений следует считать точность до 0,2 мм исходя из этого, за длину дуги для вычерчивания можно принимать ее хорду при условии, что длина дуги не превышает длину ее хорды на 0,2 мм. На основании сказанного составлена таблица по В. А. Осадченко) для спрямления дуг окружностей [c.62]
Деление на семь п более частей рекомендуется производить построением с исрользованием специальной таблицы. Допустим, окружность диаметром 112,7 мм Фо) (рис. 87) необходимо разделить на п равных частей. Для этого величину Оо умножают на соответствующий коэффициент а, взятый из табл. 5. Это произведение равно длине хорды 5, соответствующей расстоянию между двумя соседними точками данной окружности. Для повышения точности разметки целесообразно расчет длины хорды вести не по [c.146]
Теплоты образования 2 — 304 Химия 2 — 269—315 Хлорметил — Свойства 2 — 97 Ходовые посадки для древесины 5 — 621 Холод искусственный — Производство — Термодинамика 2 — 97 Холодильные агенты 2 — 97, 98 Холодильные машины 2—103—105 Хомутики металлокерамическне 5 — 261 Хорды — Длины — Таблицы 1—37 Хранение моделей 5 — 23 — опок 5 — 19
[c. 491]
491]
Деление окружности на произвольное число равных частей. Разделить окрулсность на любое число равных частей можно, пользуясь таблицей хорд (табл. 4), приведенной ниже, в которой дается длина хорды в зависимости от числа сторон правильного многоугольника, вписанного в окружность, диаметр которой с1. [c.36]
В второй части таблицы (данные для контроля) приводятся размеры и от-клонемя для контроля взаимного положения разноименных п(эофилей зубьев по одном з следующих вариантов 1) постоянная хорда зуба с и в ысота до постоянной хомы Ьс й) длина общей нормали 1 3) толщина по хорде зуба и высота до хор ы Ьау 4) торцовый азмер по роликам (шарикам) М и диаметр ролика (шарика) О, и Яс определяется по табл. 5.29. [c.357]
Как найти радиус окружности, если задана длина хорды
О «Как найти радиус окружности при заданной длине хорды»
Как найти радиус окружности, если задана длина хорды?
Здесь мы увидим, как найти радиус окружности, если задана длина хорды.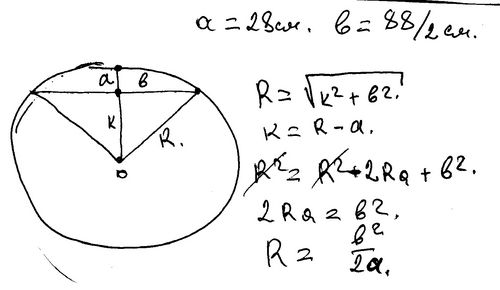
Чтобы найти длину хорды, мы можем использовать следующую теорему
- Перпендикуляр от центра окружности к хорде делит хорду пополам.
Пример 1:
Хорда длиной 20 см проводится на расстоянии 24 см от центра окружности. Найдите радиус круга.
Решение:
Здесь прямая OC перпендикулярна AB, которая разделяет хорду равной длины.
In Δ OCB,
OB 2 = OC 2 + BC 2
OB 2 = 24 2 + 10 2
BC 2 = 576 + 100
BC 2 = 676
BC = √676
BC = √ (26 ⋅ 26)
BC = 26 см
Следовательно, радиус круга равен 26 см.
Как найти расстояние хорды от центра?
Пример 2:
Хорда длиной 16 см проведена в окружности радиуса 10 см. Найдите расстояние хорды от центра круга.
Решение:
AB — хорда длиной 16 см.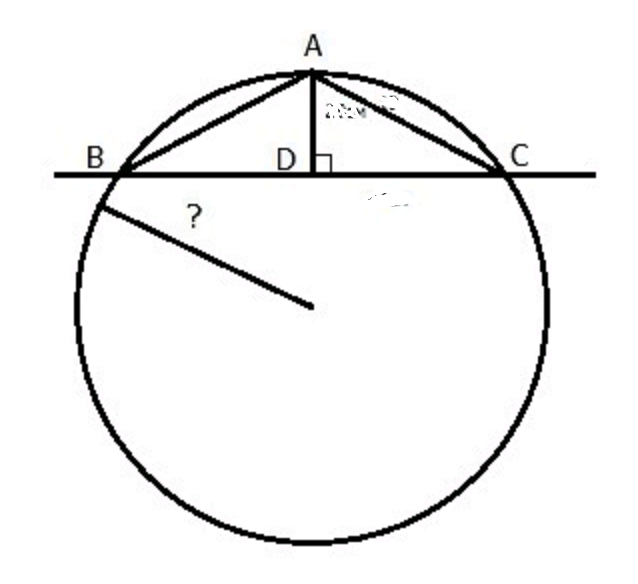
C — середина AB.
OB — радиус длиной 10 см
AB = 16 см
AC = (1/2) ⋅ 16 = 8 см
OB = 10 см
В прямоугольном треугольнике OAC.
OC 2 = OA 2 — AC 2
= √ (10 2 -8 2 )
= √ (100-64)
= √36 см
OC = 6 см
Следовательно, расстояние хорды от центра составляет 6 см
Пример 3:
Радиус окружности составляет 15 см, а длина одной из его хорды — 18 см. Найдите расстояние хорды от центра.
Решение:
AB — хорда длиной 18 см.
C — середина AB.
OB — радиус длиной 10 см
AB = 18 см
AC = (1/2) ⋅ 18 = 9 см
OB = 15 см
В прямоугольном треугольнике OCB.
OC 2 = OB 2 — BC 2
= √ (15 2 -9 2 )
= √ (225-81)
= √144
OC = 12 см
Следовательно, расстояние хорды от центра составляет 12 см.
Пройдя все, что было сказано выше, мы надеемся, что ученики поняли «Как найти радиус окружности, если задана длина хорды».
Помимо вышеперечисленного, если вы хотите узнать больше о «Как найти радиус окружности при заданной длине хорды»,
Помимо того, что дано в этом разделе, если вам нужны другие математические вещи , воспользуйтесь нашим персонализированным поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами при прямом и обратном изменении
Проблемы со словами при цене за единицу
Проблемы со словом при скорости единицы
Задачи по сравнению ставок
Преобразование обычных единиц Word задачи
Преобразование метрических единиц Word задачи
Word задачи по простому проценту
Word задачи по сложным процентам
Word задачи по типам ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами
Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи со словами с уравнениями
Проблемы со словами с линейным неравенством
ЗадачиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами для возрастов
Проблемы со словами из теоремы Пифагора
Процент числового слова проблемы
Проблемы со словами на постоянной скорости
Проблемы со словами на средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон рациональных функций
Область и диапазон рациональных функций функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
видение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование словесных задач в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Калькулятор площади круга
Калькулятор площади круга — расчет площади круга онлайн.Площадь круга — числовая характеристика, характеризующая размер плоскости, ограниченной линией окружности. Площадь круга может быть вычислена с использованием числа пи и радиуса круга или других известных входных данных. Наш калькулятор поможет вам бесплатно рассчитать площадь круга онлайн или проверить уже выполненные расчеты.
Площадь круга может быть вычислена с использованием числа пи и радиуса круга или других известных входных данных. Наш калькулятор поможет вам бесплатно рассчитать площадь круга онлайн или проверить уже выполненные расчеты.
Таблица с формулами площади круга (в конце страницы)
— Вычисление (показано) (скрыта)
— примечания (показаны) (скрыта)
1
Площадь окружности по радиусу
… подготовка …
r — радиус
2
Площадь окружности через диаметр
… подготовка …
D — диаметр
3
Площадь круга по окружности
… подготовка …
— длина окружности
4
Площадь круга, проходящего через квадрат, вписанного в круг
… подготовка …
a — боковой
5
Площадь круга, вписанного в квадрат
… подготовка …
A — боковой
6
Площадь круга, описанного вокруг произвольного треугольника
Эта формула применима только в том случае, если круг можно описать вокруг треугольника, то есть все три вершины треугольника должны лежать на линии круга. Треугольник в этом случае может быть любым.
Треугольник в этом случае может быть любым.
Чтобы вычислить площадь круга, сначала вычислите полупериметр треугольника
… подготовка …
a — боковой
b — боковой
c — боковой
7
Площадь круга, описанного рядом с равносторонним треугольником
… подготовка …
a — боковой
8
Площадь круга, описанного вокруг равностороннего треугольника, рассчитывается по высоте треугольника
… подготовка …
h — высота
9
Площадь круга около равнобедренного треугольника
… подготовка …
a — боковой
b — цоколь
10
Площадь круга, описанного около прямоугольного треугольника
… подготовка …
a — боковой
b — боковой
11
Площадь круга, вписанного в равнобедренный треугольник
. .. подготовка …
.. подготовка …
a — боковой
b — цоколь
12
Площадь круга, вписанного в равнобедренный треугольник, вычисленная по сторонам треугольника и углу между ними
… подготовка …
b — боковой
α — угол между сторонами
13
Площадь круга, вписанного в прямоугольный треугольник
… подготовка …
a — боковой
b — боковой
c — боковой
14
Площадь круга, вписанного в прямоугольный треугольник, вычисленная по стороне и углу
… подготовка …
b — боковой
α — угол при основании
15
Площадь круга, вписанного в равносторонний треугольник
… подготовка …
a — боковой
16
Площадь круга, вписанного в равнобедренную трапецию, рассчитывается от основания трапеции и угла при основании
. .. подготовка …
.. подготовка …
b — боковой
α — угол при основании
17
Площадь описанного круга около равнобедренной трапеции, вычисленная по сторонам трапеции, ее диагонали и основанию
Чтобы вычислить площадь круга, сначала вычислите полупериметр треугольника ABC
… подготовка …
a — боковой
c — боковой
d — диагональ
18
Площадь описываемого круга рядом с прямоугольником
… подготовка …
a — боковой
b — боковой
19
Площадь круга, описанного рядом с правильным многоугольником
… подготовка …
a — боковой
N — количество сторон многоугольника
20
Площадь круга, описанного около правильного шестиугольника
. .. подготовка …
.. подготовка …
a — боковой
Примечание:
Если в исходных данных угол указан в радианах, то для преобразования в градусы можно использовать формулу: 1 радиан × (180 / π) ° = 57,296 °
Таблица с формулами площади круга
| Два аккорда | 2020-04-14 | |||
| От Фрэнка: Как найти длину радиуса круга, если вы знаете длины двух хордов Ответил Пенни Ном. | ||||
| Круг в квадрате | 2020-04-02 | |||
| От Сабры: Здравствуйте, у меня в 7 классе есть двойняшки, которые учатся находить окружность кругов.  Я изо всех сил пытаюсь понять, как
помогите моим детям найти ответ на этот вопрос: Я изо всех сил пытаюсь понять, как
помогите моим детям найти ответ на этот вопрос:У Тай есть квадратный кусок желтого войлока площадью 81 квадратные дюймы. Она хочет вырезать как можно больший круг из материал для создания солнца для ее арт-проекта. Какая площадь войлока круг? Используйте 3,14 для числа пи. При необходимости округлите до ближайшей сотой. Я не был уверен, смогу ли я найти область круга, найдя площадь квадрата или какие шаги нам нужно было выполнить, чтобы найти ответ.Когда я увижу, как шаг за шагом решается одна, я обычно может помочь им вместе с похожими вопросами. Ответил Пенни Ном. | ||||
| Центр и радиус окружности | 2020-03-25 | |||
| От Райли: , значит, он говорит: найдите центр и радиус круга ниже x ^ 2 + (y-6) ^ 2 = 121 Мне нужна помощь в изучении решения этого Ответил Пенни Ном.  | ||||
| Окружность, точка и касательная | 31.12.2019 | |||
| От Фейсала: Круг имеет радиус 10 единиц и проходит через точку (5, -16). Ось x — это касательная к окружности. Найдите возможные уравнения круга? Ответил Пенни Ном. | ||||
| Центр круга | 2019-10-24 | |||
| От Патрика: Я пытаюсь быстро найти центр круга, который будет касаться трех точек равнобедренного треугольника. Известные размеры — длина основания треугольника и высота от верхней точки до середины основания.  Заранее спасибо, С уважением, Патрик Ответил Пенни Ном. | ||||
| Периметр отрезка круга | 18.10.2019 | |||
| От Арвина: Радиус круга равен 17 см.Хорда XY находится на расстоянии 9 см от центра и делит круг на два сегмента. Найдите периметр второстепенного сегмента. Ответил Пенни Ном. | ||||
| Почему у круга большая площадь? | 2019-09-16 | |||
| От ученика: для круга и квадрата с одинаковым периметром, почему круг имеет большую площадь Я ищу интуитивное объяснение, а не вычислительное. Ответил Харли Вестон. | ||||
| Радиус круга заданной площади | 2019-08-14 | |||
| От shelby: Каков радиус круга площадью 803,84 см2? Мне также нужны примеры того, как вы получили ответ. Ответил Пенни Ном. | ||||
| Сколько линий симметрии у круга? | 2019-05-28 | |||
| От raji: сколько линий симметрии у круга ??? Ответил Пенни Ном. | ||||
| Два круга | 2019-05-23 | |||
| От Армана: Две концентрические окружности имеют центры в точка C.  Радиус меньшего круга равен
8 см. Длина хорды AB составляет 26 см и
касается меньшего круга. Что
окружность большего круга? Радиус меньшего круга равен
8 см. Длина хорды AB составляет 26 см и
касается меньшего круга. Что
окружность большего круга? Ответил Пенни Ном. | ||||
| Круг вписанный в треугольник | 2019-04-28 | |||
| Из Дакши: O — центр вписанного круга в треугольник ABC 30-60-90, расположенный под прямым углом к C. Если окружность касается AB в точке D, то угол COD равен . Ответил Пенни Ном. | ||||
| Круг с круглым отверстием | 2019-03-11 | |||
| От Sue: Моя малышка задается вопросом, можно ли описать круг с круглым отверстием как неправильный полукруг.  Поскольку он имеет 2 стороны, но не стандартной формы. Не могли бы вы поделиться своими мыслями ?? Ответил Пенни Ном. | ||||
| Равносторонний треугольник, вписанный в окружность | 2019-01-29 | |||
| От Пенни: Какова длина каждой стороны самого большого равностороннего треугольника, который умещается внутри круга диаметром 3 дюйма? Ответил Пенни Ном.2theta, почему это 1/2? Пожалуйста, объясните концептуально, а не алгебраически. Ответил Пенни Ном. | ||||
| Сформируйте конус из круга сектора | 12. 08.2018 08.2018 | |||
| Из Тинаше: 216 сектор окружности радиусом 5 см изгибается в виде конуса. Найдите радиус основания конуса и его вертикальный угол. Ответил Пенни Ном. | ||||
| Круг, вписанный в правильный многоугольник | 12.07.2018 | |||
| Из Naveen: Радиус вписанной окружности для n-стороннего правильного многоугольника на стороне a равен? Пожалуйста, предоставьте доказательство Ответил Пенни Ном. | ||||
| Касательная к окружности | 2018-06-10 | |||
| От Bellle: Определите уравнение окружности, имеющей центр в (3,1) и касательную 3x-4y + 5 = 0 Ответил Пенни Ном.  | ||||
| Семь касательных окружностей | 2018-04-23 | |||
| От Доменика: Как вычислить описанные и вписанные окружности, образованные семью окружностями диаметром 0,019685, расположенными по окружности, причем все семь окружностей касаются друг друга? Ответил Пенни Ном. | ||||
| Круг вписанный в четверть круга | 2018-04-16 | |||
| From abhijeet: ABC — это четверть круга, в который вписан меньший круг.если AB = 1 см, тогда найдите радиус меньшего круга Ответил Пенни Ном.  ©2013-2025 «АртЛига». Конкурс в области промышленного дизайна мебели. | ||||

 Опа-на! Не путаем диаметр и радиус!
Опа-на! Не путаем диаметр и радиус!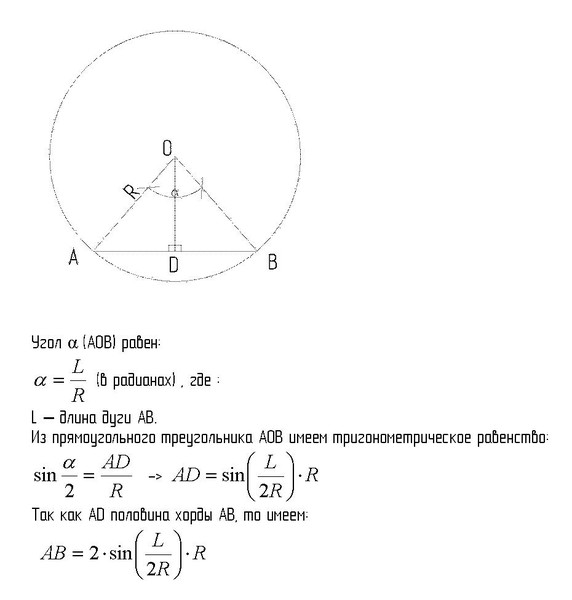 Углы на плоскости
Углы на плоскости Верно и обратное
Верно и обратное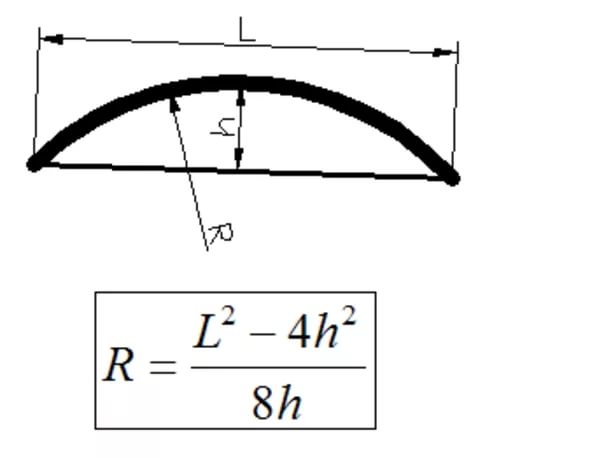
 Спасибо
Спасибо