Зависимость скорости от давления воды: Зависимость Давления Жидкости от Скорости ее Течения

ЧАРУЮЩИЕ ТАЙНЫ ЖИДКОСТИ | Наука и жизнь

Существует поразительная возможность овладеть предметом математически, не понимая существа дела.
А. Эйнштейн

Эксперимент остается навсегда.
П. Л. Капица

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

‹

›

Открыть в полном размере

Тысячи лет люди наблюдают вечно изменчивое течение воды и пытаются разгадать ее тайну. Первоклассные физики и математики ломали и продолжают ломать головы, стараясь понять природу и прихотливое поведение потока воды. Но вступив в XXI век, мы с сожалением должны констатировать, что с конца XIX столетия — времени наивысшего расцвета науки о движении сплошных сред (гидродинамики в случае жидкости и аэродинамики в случае газа) — мы очень мало продвинулись в понимании природы этого вечно меняющегося течения.

Все основные законы течения жидкости (для краткости везде будет говориться о жидкости, хотя, за некоторым исключением, те же закономерности присущи и газу) были открыты до первой половины XIX столетия. Перечислим их.

ПОСТОЯНСТВО ПОТОКА МАССЫ ЖИДКОСТИ

Его еще называют законом неразрывности, законом непрерывности, уравнением сплошности жидкости или законом сохранения вещества в гидродинамике. По существу, этот закон был открыт Б. Кастелли в 1628 году. Он установил, что скорость течения жидкости в трубах обратно пропорциональна площади их поперечного сечения. Другими словами, чем уже сечение канала, тем с большей скоростью движется в нем жидкость.

ВЯЗКОСТЬ ЖИДКОСТИ

И. Ньютон (конец XVII века) экспериментально установил, что любой жидкости свойственна вязкость, то есть внутреннее трение. Вязкость приводит к возникновению сил трения между движущимися с различными скоростями слоями жидкости, а также между жидкостью и омываемым ею телом. Им же было установлено, что сила трения пропорциональна коэффициенту вязкости жидкости и градиенту (перепаду) скорости потока в направлении, перпендикулярном его движению. Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.

В силу вязкого трения скорость жидкости на поверхности омываемого ею тела всегда равна нулю. Это совсем не очевидно, но тем не менее подтверждается во множестве экспериментов.

Опыт.

Убедимся, что скорость газа на поверхности обдуваемого им тела равна нулю.

Возьмем вентилятор и припудрим его лопасти пылью. Включим вентилятор в сеть и через несколько минут выключим. Пыль на лопастях как была, так и осталась, хотя вентилятор вращался с довольно большой скоростью и она должна была бы слететь.

Омывая лопасти вентилятора с большой скоростью, поток воздуха на их поверхности имеет нулевую скорость, то есть неподвижен. Поэтому пыль на них и остается. По этой же причине с гладкой поверхности стола легко можно сдуть крошки, а пыль приходится вытирать.

#1# ИЗМЕНЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В ЗАВИСИМОСТИ ОТ СКОРОСТИ ЕЕ ДВИЖЕНИЯ.

Д. Бернулли в своей книге «Гидродинамика» (1738) получил для идеальной жидкости, не обладающей вязкостью, математическую формулировку закона сохранения энергии в жидкости, который носит теперь название уравнения Бернулли. Оно связывает давление в потоке жидкости с ее скоростью и утверждает, что давление жидкости при ее движении меньше там, где сечение потока

S меньше, а скорость жидкости соответственно больше. Вдоль трубки тока, которую можно мысленно выделить в спокойном безвихревом потоке, сумма статического давления , динамического ρV²/2, вызванного движением жидкости плотностью ρ, и давления ρgh столба жидкости высотой h остается постоянной:

#13#

Это уравнение играет фундаментальную роль в гидродинамике, несмотря на то, что оно, строго говоря, справедливо только для идеальной, то есть не имеющей вязкости, жидкости.

#2#

Опыт 1. Убедимся, что чем выше скорость воздуха, тем меньше давление в нем.

Зажжем свечу и через тонкую трубочку, например для коктейля, сильно дунем в нее так, чтобы струйка воздуха прошла примерно на расстоянии 2 см от пламени. Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.

#3# Лабораторный водоструйный насос. В струе воды из крана создается разрежение, которое выкачивает воздух из колбы.

Почему? Согласно уравнению Бернулли, чем выше скорость потока, тем меньше давление в нем. Воздух выходит из трубочки с большой скоростью, так что давление в струе воздуха меньше, чем в окружающем свечу неподвижном воздухе. Перепад давления при этом направлен в сторону выходящего из трубочки воздуха, что и отклоняет к ней пламя свечи.

#4# Принцип работы пульверизатора: атмосферное давление выжимает жидкость в струю воздуха, где давление ниже.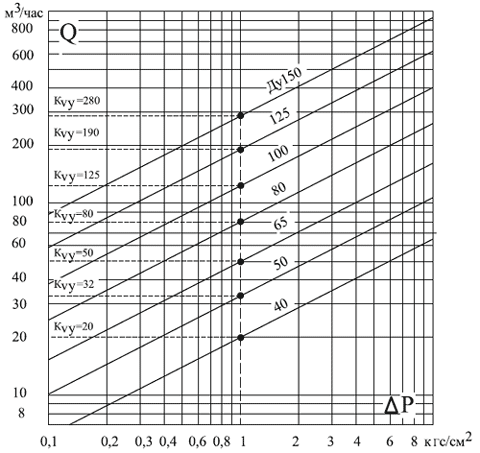

На этом принципе работают пульверизаторы, струйные насосы и автомобильные карбюраторы: жидкость втягивается в поток воздуха, давление в котором ниже атмосферного.

Опыт 2. Возьмем лист писчей бумаги за верхние края, поднесем его к стене и удержим на расстоянии примерно 3-5 см от стены. Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.

#5#

Уравнение Бернулли объясняет также классический опыт с трубой переменного сечения. В силу закона неразрывности для сохранения потока массы жидкости в суженной части трубы ее скорость должна быть выше, чем в широкой. Следовательно, давление выше там, где труба шире, и ниже там, где она уже.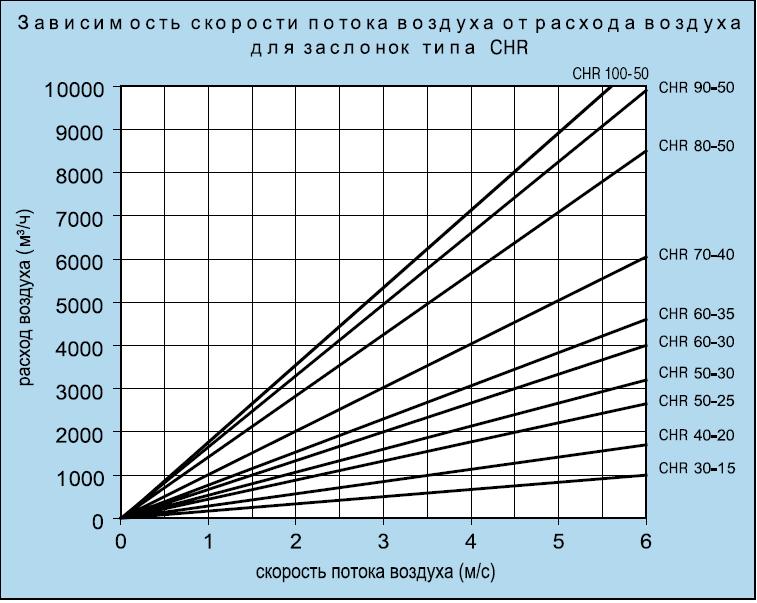

На этом принципе работает устройство для измерения скорости или расхода жидкости — трубка Вентури.

Падение внутреннего давления в потоке — хорошо проверенный экспериментальный факт, тем не менее он, вообще говоря, парадоксален. Действительно, интуитивно ясно, что жидкость, «протискиваясь» из широкой части трубы в узкую, «сжимается», а это должно привести к росту давления в ней. Такому поведению жидкости в настоящее время нет объяснения даже на молекулярном уровне, по крайней мере, автор его нигде не обнаружил.

#6# СОПРОТИВЛЕНИЕ, ИСПЫТЫВАЕМОЕ ТЕЛОМ ПРИ ДВИЖЕНИИ В ЖИДКОСТИ

Существование сопротивления среды было обнаружено еще Леонардо да Винчи в XV столетии. Мысль, что сопротивление жидкости движению тела пропорционально скорости тела, впервые высказал английский ученый Дж. Уиллис. Ньютон во втором издании своей знаменитой книги «Математические начала натуральной философии» установил, что сопротивление состоит из двух членов, одного — пропорционального квадрату скорости и другого — пропорционального скорости.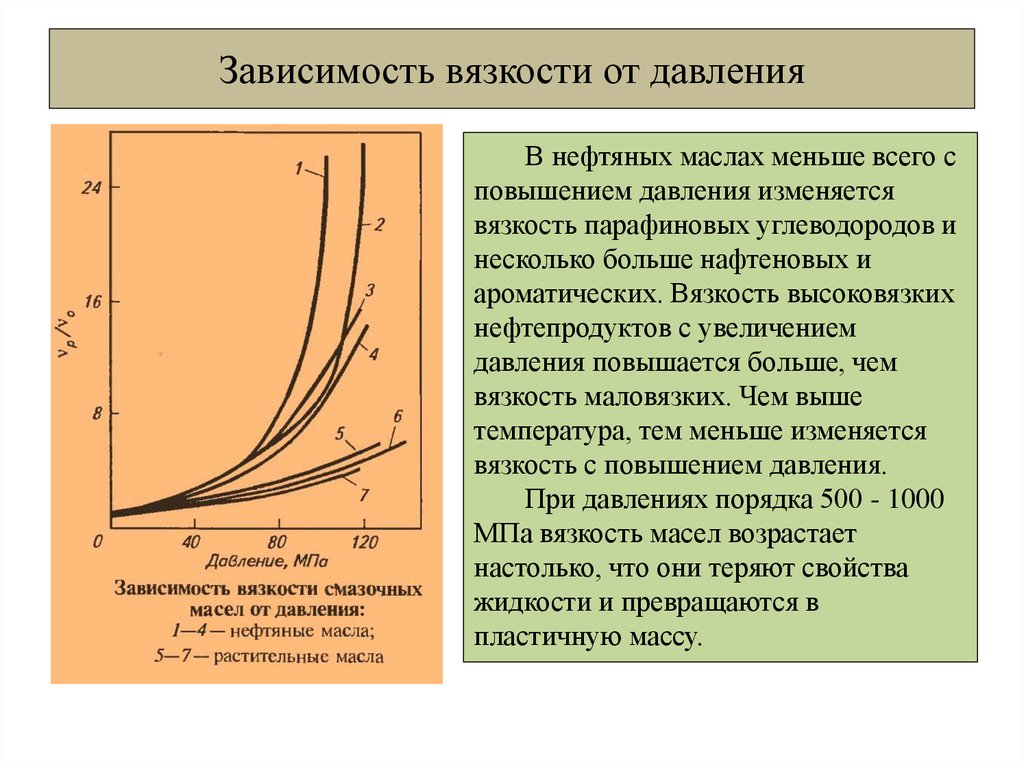

Там же Ньютон сформулировал теорему о пропорциональности сопротивления максимальной площади сечения тела, перпендикулярного направлению потока. Силу сопротивления тела, медленно движущегося в вязкой жидкости, рассчитал в 1851 году Дж. Стокс. Она оказалась пропорциональной коэффициенту вязкости жидкости, первой степени скорости тела и его линейным размерам.

Необходимо отметить, что сопротивление жидкости движущемуся в нем телу в значительной мере обусловливается именно наличием вязкости. В идеальной жидкости, в которой вязкость отсутствует, сопротивление вообще не возникает.

Опыт 1. Посмотрим, как возникает сопротивление движущегося в жидкости тела. Хотя в опыте тело неподвижно, а движется воздух, результата это не меняет. Какая разница, что движется — тело в воздухе или воздух относительно неподвижного тела?

#7#

Возьмем свечу и коробок спичек. Зажжем свечу, поставим перед ней на расстоянии примерно 3 см коробок и сильно дунем на него.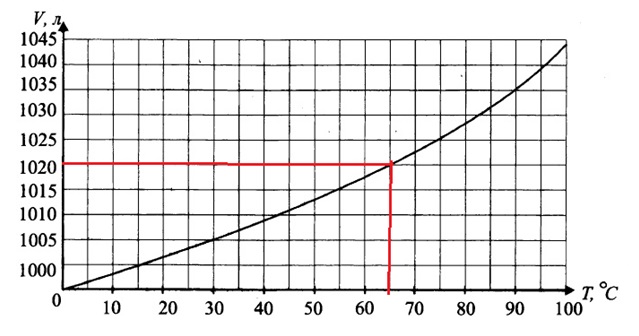 Пламя свечи отклоняется к коробку. Это означает, что позади коробка давление стало меньше, чем позади свечи, и разность давлений направлена по движению потока воздуха. Следовательно, тело при движении в воздухе или жидкости испытывает торможение.

Поток воздуха набегает на переднюю поверхность коробка, огибает его по краям и не смыкается позади, а отрывается от препятствия. Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен. Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.

Сопротивление зависит от скорости движения тела в жидкости, свойств жидкости, формы тела и его размеров. Важную роль в создании сопротивления играет форма задней стороны движущегося тела. Позади плоского тела возникает пониженное давление, поэтому сопротивление можно уменьшить, предотвратив срыв потока. Для этого телу придают обтекаемую форму. Поток плавно огибает тело и смыкается непосредственно за ним, не создавая области пониженного давления.

Опыт 2. Чтобы продемонстрировать различный характер обтекания, а следовательно, и сопротивле ния тел различной формы, возьмем шар, например мяч для пинг-понга или тенниса, приклеим к нему бумажный конус и поставим за ним горящую свечу.

#8#

Повернем тело шариком к себе и подуем на него. Пламя отклонится от тела. Теперь повернем тело к себе острым концом и снова подуем. Пламя отклоняется к телу. Этот опыт показывает, что форма задней поверхности тела определяет направление перепада давления позади нее, а следовательно , и сопротивление тела в потоке воздуха.

В первом опыте пламя отклоняется от тела; это означает, что перепад давления направлен по потоку. Струя воздуха плавно обтекает тело, смыкается за ним и далее движется обычной струей, которая отклоняет пламя свечи назад и может даже задуть его. Во втором опыте пламя отклоняется к телу — как и в эксперименте с коробком, позади тела создается разрежение, перепад давления направлен против потока. Следовательно, в первом опыте сопротивление тела меньше, чем во втором.

ПАДЕНИЕ ДАВЛЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ ПРИ ЕЕ ДВИЖЕНИИ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯ

Опыт показывает, что давление в жидкости, текущей по трубе постоянного сечения, падает вдоль трубы по течению: чем дальше от начала трубы, тем оно ниже. Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.

Опыт. Возьмем резиновую или пластиковую трубку постоянного сечения и такого диаметра, чтобы ее можно было насадить на носик водопроводного крана. Сделаем в трубке два отверстия и откроем воду. Из отверстий начнут бить фонтанчики, причем высота ближнего к крану фонтанчика будет заметно выше, чем расположенного дальше по потоку. Это показывает, что давление воды в ближайшем к крану отверстии выше, чем в дальнем: оно падает вдоль трубы в направлении потока.

#9#

Объяснение этого явления на молекулярном уровне автору не известно. Поэтому приведем классическое объяснение. Выделим в жидкости маленький объем, ограниченный стенками трубки и двумя сечениями слева и справа. Так как жидкость течет по трубке равномерно, то разность давлений слева и справа от выделенного объема должна быть уравновешена силами трения между жидкостью и стенками трубки. Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.

На первый взгляд приведенное объяснение удовлетворительно. Однако возникают вопросы, ответа на которые пока нет.

1. Согласно уравнению Бернулли, уменьшение давления в жидкости при ее движении вдоль трубы должно означать, что скорость ее, наоборот, должна расти вдоль потока, то есть течение жидкости должно ускоряться. Но этого не может быть в силу закона неразрывности.

2. Силы трения между стенками трубы и жидкостью должны в принципе тормозить ее. Если это так, то при торможении скорость жидкости вдоль канала должна падать, что в свою очередь приведет к росту давления в ней по потоку. Однако внешнее давление, прокачивающее жидкость по трубе, компенсирует силы трения, заставляя жидкость течь равномерно с одинаковой по всему каналу скоростью. А раз так, то и давление жидкости вдоль канала должно быть везде одинаковым.

Итак, налицо экспериментальный факт, который легко проверить, однако объяснение его остается открытым.

ЭФФЕКТ МАГНУСА

Речь идет о возникновении силы, перпендикулярной потоку жидкости при обтекании ею вращающегося тела. Этот эффект был обнаружен и объяснен Г. Г. Магнусом (около середины XIX столетия) при изучении полета вращающихся артиллерийских снарядов и их отклонения от цели. Эффект Магнуса состоит в следующем. При вращении летящего тела близлежащие слои жидкости (воздуха) увлекаются им и также получают вращение вокруг тела, то есть начинают циркулировать вокруг него. Встречный поток рассекается телом на две части. Одна часть направлена в ту же сторону, что и циркулирующий вокруг тела поток; при этом происходит сложение скоростей набегающего и циркулирующего потоков, значит, давление в этой части потока уменьшается. Другая часть потока направлена в сторону, противоположную циркуляции, и здесь результирующая скорость потока падает, что приводит к увеличению давления. Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).

#10#

Опыт. Склеим из листа плотной бумаги цилиндр. Из доски, положенной одним краем на стопку книг, сделаем на столе наклонную плоскость и положим на нее цилиндр. Скатившись, он вроде бы должен дальше двигаться по параболе и упасть дальше от края. Однако вопреки ожидаемому траектория его движения загибается в другую сторону, и цилиндр залетает под стол. Все дело в том, что он не просто падает, а еще и вращается, создавая вокруг себя циркуляцию воздуха. Возникает избыточное давление, направленное в сторону, противоположную поступательному движению цилиндра.

#11#

Эффект Магнуса позволяет игрокам в пинг-понг и теннис отбивать «крученые» мячи, а футболистам — посылать «сухой лист», ударяя мяч по краю.

ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ ПОТОКИ

Опыт обнаруживает две совершенно разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.

Опыт. Посмотрим, как происходит переход ламинарного потока в турбулентный. Откроем кран и пустим воду сначала тоненькой струйкой, а потом все сильнее и сильнее (конечно, так, чтобы не затопить соседей). Тоненькая струйка движется плавно и спокойно. По мере того, как увеличивается напор воды, скорость струи растет, и, начиная с некоторого момента, вода в ней начинает закручиваться — возникают вихри. Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение — оно становится турбулентным.

#12# Струя воды падает в поле тяжести, испытывая ускорение. Как только скорость течения возрастает настолько, что число Рейнольдса превышает критическое значение, ламинарное течение (вверху) переходит в турбулентное. Для данного течения Re»2300.

Оценить скорость течения жидкости или газа, при которой возникает турбулентность, можно при помощи так называемого числа Рейнольдса Re = ρvl/μ, где ρ — плотность жидкости или газа, μ — их вязкость (вязкость воздуха, например, 18,5.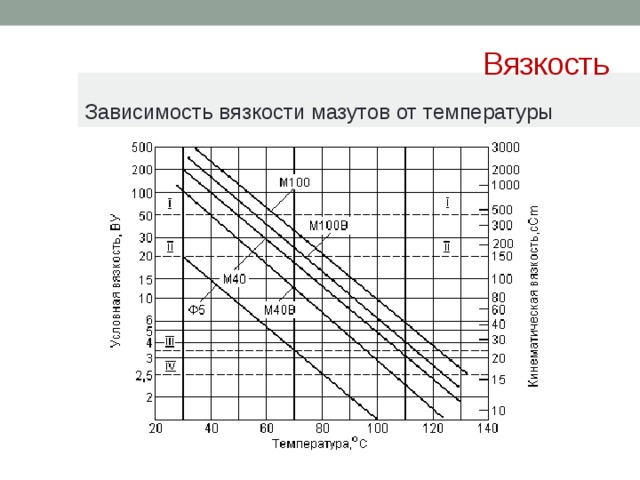 10^-6 Па.с; воды — 8,2.10^-2 Па.с), v — скорость потока, l — характерный линейный размер (диаметр трубы, длина обтекаемого тела и пр.). Для каждого вида течений существует такая критическая величина Re_кр, что при Re<Re_кр возможно только ламинарное течение, а при Re>Re_кр оно может стать турбулентым. Если измерить скорость течения воды из крана или вдоль желоба, то, исходя из приведенных значений, можно самим определить, при каком значении Re_кр в потоке начинает развиваться турбулентность. Оно должно быть порядка 2000.

Расчет диаметра трубопровода по расходу, зависимость расхода от давления

Для того чтобы правильно смонтировать конструкцию водопровода, начиная разработку и планирование системы, необходимо рассчитать расход воды через трубу.

От полученных данных зависят основные параметры домашнего водовода.

В этой статье читатели смогут познакомиться с основными методиками, которые помогут им самостоятельно выполнить расчет своей водопроводной системы.

Содержание

• 1 Как рассчитать необходимый диаметр трубы
• 2 Подходящая скорость жидкости, в зависимости от вида трубопровода
• 3 Скорость воды в трубопроводе формула
• 4 Формула расхода воды
• 5 Зависимость расхода от давления

Как рассчитать необходимый диаметр трубы

Цель расчета диаметра трубопровода по расходу: Определение диаметра и сечения трубопровода на основе данных о расходе и скорости продольного перемещения воды.

Выполнить такой расчет достаточно сложно. Нужно учесть очень много нюансов, связанных с техническими и экономическими данными. Эти параметры взаимосвязаны между собой. Диаметр трубопровода зависит от вида жидкости, которая будет по нему перекачиваться.

Если увеличить скорость движения потока можно уменьшить диаметр трубы. Автоматически снизится материалоемкость. Смонтировать такую систему будет намного проще, упадет стоимость работ.

Однако увеличение движения потока вызовет потери напора, которые требуют создание дополнительной энергии, для перекачки. Если очень сильно ее уменьшить, могут появиться нежелательные последствия.

С помощью формул ниже можно как рассчитать расход воды в трубе, так и, определить зависимость диаметра трубы от расхода жидкости.

Когда выполняется проектирование трубопровода, в большинстве случаев, сразу задается величина расхода воды. Неизвестными остаются две величины:

•  Диаметр трубы;
• Скорость потока.

Сделать полностью технико-экономический расчет очень сложно. Для этого нужны соответствующие инженерные знания и много времени. Чтобы облегчить такую задачу при расчете нужного диаметра трубы, пользуются справочными материалами. В них даются значения наилучшей скорости потока, полученные опытным путем.

Итоговая расчетная формула для оптимального диаметра трубопровода выглядит следующим образом:

d = √(4Q/Πw)
Q – расход перекачиваемой жидкости, м3/с
d – диаметр трубопровода, м
w – скорость потока, м/с

Подходящая скорость жидкости, в зависимости от вида трубопровода

Прежде всего учитываются минимальные затраты, без которых невозможно перекачивать жидкость. Кроме того, обязательно рассматривается стоимость трубопровода.

При расчете, нужно всегда помнить об ограничениях скорости двигающейся среды. В некоторых случаях, размер магистрального трубопровода должен отвечать требованиям, заложенным в технологический процесс.

Когда делаются предварительные расчеты, изменение давление в расчет не берется. За основу проектирования технологического трубопровода берется допустимая скорость.

Когда в проектируемом трубопроводе существуют изменения направления движения, поверхность трубы начинает испытывать большое давление, направленное перпендикулярно движению потока.

Такое увеличение связано с несколькими показателями:

• Скорость жидкости;
• Плотность;
• Исходное давление (напор).

Причем скорость всегда находится в обратной пропорции к диаметру трубы. Именно поэтому для высокоскоростных жидкостей требуется правильный выбор конфигурации, грамотный подбор габаритов трубопровода.

К примеру, если перекачивается серная кислота, значение скорости ограничивается до величины, которая не станет причиной появления эрозия на стенках трубных колен. В результате структура трубы никогда не будет нарушена.

Скорость воды в трубопроводе формула

Объёмный расход V (60м³/час или 60/3600м³/сек) рассчитывается как произведение скорости потока w на поперечное сечение трубы S (а поперечное сечение в свою очередь считается как S=3.14 d²/4): V = 3.14 w d²/4. Отсюда получаем w = 4V/(3.14 d²). Не забудьте перевести диаметр из миллиметров в метры, то есть диаметр будет 0.159 м.

Формула расхода воды

В общем случае методология измерения расхода воды в реках и трубопроводах основана на упрощённой форме уравнения непрерывности, для несжимаемых жидкостей:

Расход воды через трубу таблица

Зависимость расхода от давления

Нет такой зависимости расхода жидкости от давления, а есть — от перепада давления. Формула выводится просто. Имеется общепринятое уравнение перепада давления при течении жидкости в трубе Δp = (λL/d) ρw²/2, λ — коэффициент трения (ищется в зависимости от скорости и диаметра трубы по графикам или соответствующим формулам), L — длина трубы, d — ее диаметр, ρ -плотность жидкости, w — скорость.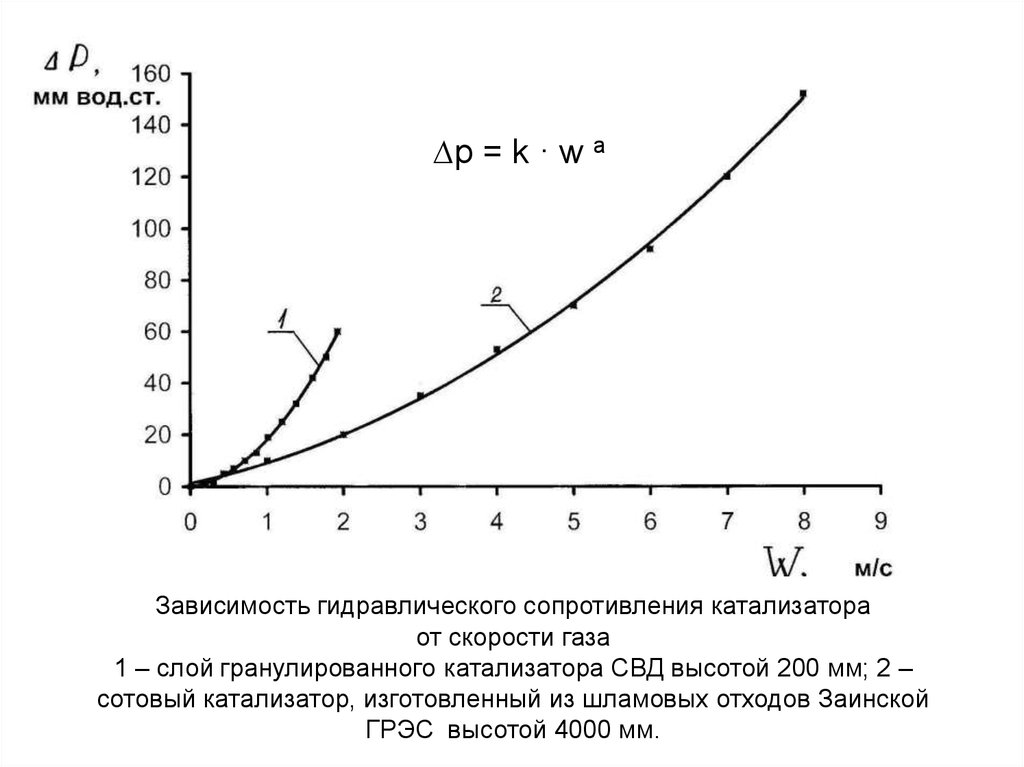 5/λ/L)/4, SQRT — квадратный корень.

Коэффициент трения ищется подбором. Вначале задаете от фонаря некоторое значение скорости жидкости и определяете число Рейнольдса Re=ρwd/μ, где μ — динамическая вязкость жидкости (не путайте с кинематической вязкостью, это разные вещи). По Рейнольдсу ищете значения коэффициента трения λ = 64/Re для ламинарного режима и λ = 1/(1.82 lgRe — 1.64)² для турбулентного (здесь lg — десятичный логарифм). И берете то значение, которое выше. После того, как найдете расход жидкости и скорость, надо будет повторить весь расчет заново с новым коэффициентом трения. И такой перерасчет повторяете до тех пор, пока задаваемое для определения коэффициента трения значение скорости не совпадет до некоторой погрешности с тем значением, что вы найдете из расчета.

Похожие статьи:

гидродинамика — Зависит ли скорость потока между двумя давлениями от абсолютной или относительной разницы давлений?

Спросил 6 лет, 8 месяцев назад

Изменено 6 лет, 8 месяцев назад

Просмотрено 368 раз

$\begingroup$

Представьте, что у вас есть барокамера, которая разделена съемной стенкой на две равные части.

Сценарий A) Давление воздуха слева 1 бар, справа 2 бара.
Сценарий Б) Давление воздуха слева 10 бар, справа 11 бар.

Абсолютная разница давлений между двумя сторонами одинакова (1 бар в обоих случаях). Разница относительного давления больше в сценарии A, чем в сценарии B.

Когда стена в середине удалена, воздух течет с правой стороны на левую. Теперь, скорость потока воздуха одинакова для обоих сценариев или больше в сценарии А? Интуитивно я предполагаю, что скорость потока больше в сценарии А (из-за большей разности относительных давлений), но я не могу подкрепить это веским аргументом.

Что происходит?

• гидродинамика
• давление

$\endgroup$

1

$\begingroup$

Итак, давайте посмотрим на уравнения для первоначально покоящегося потока:

Итак, если предположить, что плотность в потоке постоянна, вы получите:

$$ \frac{\partial u}{\partial t} = -\frac{1}{\rho}\frac{\partial p }{\частичный х}$$

, и поэтому вы можете видеть, что в обоих ваших случаях градиент давления имеет одинаковый размер независимо от величины давления. Итак, если ваш случай B более горячий, так что две плотности между случаями A и B одинаковы, ускорение должно быть одинаковым.

С другой стороны, если ваши температуры одинаковы, то ваше ускорение будет выше в случае A, потому что плотность ниже.

Так как ваша система является замкнутой и неустойчивой, нет смысла смотреть на общую скорость потока, потому что она постоянно меняется. Но ускорение будет меняться в зависимости от того, как вы меняли давление. 92$$

где $\Delta P = P_0 — P_s$ где-то вдоль линии тока. Итак, мы снова видим, что скорость зависит от изменения давления и плотности, и мы возвращаемся к тому же аргументу, что и выше.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

уравнение Бернулли — Напор воды и скорость воды Шланг и резервуар были неизвестны, поэтому я бы использовал лучшую модель, т.

Е. Уравнение потока Пуазейля.

Уравнение течения Пуазейля для движения жидкости в трубе утверждает, что:

$$\Delta p = \frac {8L \eta \pi v_{out}}{A}$$ то есть 9{-1}$$

, что довольно близко к истинному значению.

Обратите внимание, что значение, которое мы здесь получаем, не совсем точное, потому что (как утверждает Википедия):

• Уравнение не выполняется вблизи входа в трубу.

• Уравнение не работает в пределе низкой вязкости, широкой и/или короткой трубы. Низкая вязкость или широкая труба могут привести к турбулентному потоку, что делает необходимым использование более сложных моделей, таких как уравнение Дарси-Вейсбаха.

---

$$\pmb { \underline { \text {Простой случай}}}(L_{Труба}=0)$$

Радиус отверстия довольно мал по сравнению с радиусом резервуара и, следовательно, может легко пренебречь, не вызывая каких-либо отклонений в скорости воды, выходящей из отверстия.