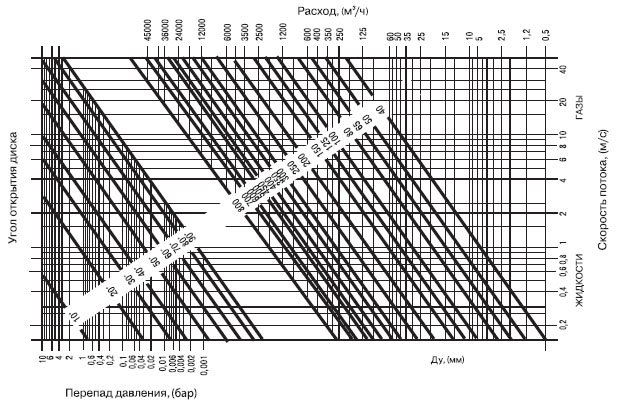
Расчет диаметра трубопровода по расходу, зависимость расхода от давления
Для того чтобы правильно смонтировать конструкцию водопровода, начиная разработку и планирование системы, необходимо рассчитать расход воды через трубу.
От полученных данных зависят основные параметры домашнего водовода.
В этой статье читатели смогут познакомиться с основными методиками, которые помогут им самостоятельно выполнить расчет своей водопроводной системы.
Как рассчитать необходимый диаметр трубы
Цель расчета диаметра трубопровода по расходу: Определение диаметра и сечения трубопровода на основе данных о расходе и скорости продольного перемещения воды.
Выполнить такой расчет достаточно сложно. Нужно учесть очень много нюансов, связанных с техническими и экономическими данными. Эти параметры взаимосвязаны между собой. Диаметр трубопровода зависит от вида жидкости, которая будет по нему перекачиваться.
Если увеличить скорость движения потока можно уменьшить диаметр трубы.
Однако увеличение движения потока вызовет потери напора, которые требуют создание дополнительной энергии, для перекачки. Если очень сильно ее уменьшить, могут появиться нежелательные последствия.
С помощью формул ниже можно как рассчитать расход воды в трубе, так и, определить зависимость диаметра трубы от расхода жидкости.
Когда выполняется проектирование трубопровода, в большинстве случаев, сразу задается величина расхода воды. Неизвестными остаются две величины:
- Диаметр трубы;
- Скорость потока.
Сделать полностью технико-экономический расчет очень сложно. Для этого нужны соответствующие инженерные знания и много времени. Чтобы облегчить такую задачу при расчете нужного диаметра трубы, пользуются справочными материалами. В них даются значения наилучшей скорости потока, полученные опытным путем.
Итоговая расчетная формула для оптимального диаметра трубопровода выглядит следующим образом:d = √(4Q/Πw)
Q – расход перекачиваемой жидкости, м3/с
d – диаметр трубопровода, м
w – скорость потока, м/с
Подходящая скорость жидкости, в зависимости от вида трубопровода
Прежде всего учитываются минимальные затраты, без которых невозможно перекачивать жидкость. Кроме того, обязательно рассматривается стоимость трубопровода.
Кроме того, обязательно рассматривается стоимость трубопровода.
При расчете, нужно всегда помнить об ограничениях скорости двигающейся среды. В некоторых случаях, размер магистрального трубопровода должен отвечать требованиям, заложенным в технологический процесс.
На габариты трубопровода влияют также возможные скачки давления.
Когда делаются предварительные расчеты, изменение давление в расчет не берется. За основу проектирования технологического трубопровода берется допустимая скорость.
Когда в проектируемом трубопроводе существуют изменения направления движения, поверхность трубы начинает испытывать большое давление, направленное перпендикулярно движению потока.
Такое увеличение связано с несколькими показателями:
- Скорость жидкости;
- Плотность;
- Исходное давление (напор).
Причем скорость всегда находится в обратной пропорции к диаметру трубы. Именно поэтому для высокоскоростных жидкостей требуется правильный выбор конфигурации, грамотный подбор габаритов трубопровода.
Именно поэтому для высокоскоростных жидкостей требуется правильный выбор конфигурации, грамотный подбор габаритов трубопровода.
К примеру, если перекачивается серная кислота, значение скорости ограничивается до величины, которая не станет причиной появления эрозия на стенках трубных колен. В результате структура трубы никогда не будет нарушена.
Скорость воды в трубопроводе формула
Объёмный расход V (60м³/час или 60/3600м³/сек) рассчитывается как произведение скорости потока w на поперечное сечение трубы S (а поперечное сечение в свою очередь считается как S=3.14 d²/4): V = 3.14 w d²/4. Отсюда получаем w = 4V/(3.14 d²). Не забудьте перевести диаметр из миллиметров в метры, то есть диаметр будет 0.159 м.Формула расхода воды
В общем случае методология измерения расхода воды в реках и трубопроводах основана на упрощённой форме уравнения непрерывности, для несжимаемых жидкостей:
Расход воды через трубу таблица
Зависимость расхода от давления
Нет такой зависимости расхода жидкости от давления, а есть — от перепада давления. 5/λ/L)/4, SQRT — квадратный корень.
5/λ/L)/4, SQRT — квадратный корень.
Коэффициент трения ищется подбором. Вначале задаете от фонаря некоторое значение скорости жидкости и определяете число Рейнольдса Re=ρwd/μ, где μ — динамическая вязкость жидкости (не путайте с кинематической вязкостью, это разные вещи). По Рейнольдсу ищете значения коэффициента трения λ = 64/Re для ламинарного режима и λ = 1/(1.82 lgRe — 1.64)² для турбулентного (здесь lg — десятичный логарифм). И берете то значение, которое выше. После того, как найдете расход жидкости и скорость, надо будет повторить весь расчет заново с новым коэффициентом трения. И такой перерасчет повторяете до тех пор, пока задаваемое для определения коэффициента трения значение скорости не совпадет до некоторой погрешности с тем значением, что вы найдете из расчета.
Похожие статьи:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ЧАРУЮЩИЕ ТАЙНЫ ЖИДКОСТИ | Наука и жизнь
Существует поразительная возможность овладеть предметом математически,
не понимая существа дела..gif)
А. Эйнштейн
Эксперимент остается навсегда.
П. Л. Капица
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Тысячи лет люди наблюдают вечно изменчивое течение воды и пытаются разгадать ее тайну. Первоклассные физики и математики ломали и продолжают ломать головы, стараясь понять природу и прихотливое поведение потока воды. Но вступив в XXI век, мы с сожалением должны констатировать, что с конца XIX столетия — времени наивысшего расцвета науки о движении сплошных сред (гидродинамики в случае жидкости и аэродинамики в случае газа) — мы очень мало продвинулись в понимании природы этого вечно меняющегося течения. Все основные законы течения жидкости (для краткости везде будет говориться о жидкости, хотя, за некоторым исключением, те же закономерности присущи и газу) были открыты до первой половины XIX столетия. Перечислим их.
Все основные законы течения жидкости (для краткости везде будет говориться о жидкости, хотя, за некоторым исключением, те же закономерности присущи и газу) были открыты до первой половины XIX столетия. Перечислим их.
Его еще называют законом неразрывности, законом непрерывности, уравнением сплошности жидкости или законом сохранения вещества в гидродинамике. По существу, этот закон был открыт Б. Кастелли в 1628 году. Он установил, что скорость течения жидкости в трубах обратно пропорциональна площади их поперечного сечения. Другими словами, чем уже сечение канала, тем с большей скоростью движется в нем жидкость.
ВЯЗКОСТЬ ЖИДКОСТИИ. Ньютон (конец XVII века) экспериментально установил, что любой жидкости свойственна вязкость, то есть внутреннее трение. Вязкость приводит к возникновению сил трения между движущимися с различными скоростями слоями жидкости, а также между жидкостью и омываемым ею телом. Им же было установлено, что сила трения пропорциональна коэффициенту вязкости жидкости и градиенту (перепаду) скорости потока в направлении, перпендикулярном его движению. Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.
Жидкости, подчиняющиеся этому закону, называют ньютоновскими в отличие от неньютоновских жидкостей, у которых зависимость между силой вязкого трения и скоростью жидкости имеет более сложный характер.
В силу вязкого трения скорость жидкости на поверхности омываемого ею тела всегда равна нулю. Это совсем не очевидно, но тем не менее подтверждается во множестве экспериментов.
Опыт. Убедимся, что скорость газа на поверхности обдуваемого им тела равна нулю.
Возьмем вентилятор и припудрим его лопасти пылью. Включим вентилятор в сеть и через несколько минут выключим. Пыль на лопастях как была, так и осталась, хотя вентилятор вращался с довольно большой скоростью и она должна была бы слететь.
Омывая лопасти вентилятора с большой скоростью, поток воздуха на их поверхности имеет нулевую скорость, то есть неподвижен. Поэтому пыль на них и остается. По этой же причине с гладкой поверхности стола легко можно сдуть крошки, а пыль приходится вытирать.
#1# ИЗМЕНЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В ЗАВИСИМОСТИ ОТ СКОРОСТИ ЕЕ ДВИЖЕНИЯ.
Д. Бернулли в своей книге «Гидродинамика» (1738) получил для идеальной жидкости, не обладающей вязкостью, математическую формулировку закона сохранения энергии в жидкости, который носит теперь название уравнения Бернулли. Оно связывает давление в потоке жидкости с ее скоростью и утверждает, что давление жидкости при ее движении меньше там, где сечение потока S меньше, а скорость жидкости соответственно больше. Вдоль трубки тока, которую можно мысленно выделить в спокойном безвихревом потоке, сумма статического давления , динамического ρV2/2, вызванного движением жидкости плотностью ρ, и давления ρgh столба жидкости высотой h остается постоянной:
#13#Это уравнение играет фундаментальную роль в гидродинамике, несмотря на то, что оно, строго говоря, справедливо только для идеальной, то есть не имеющей вязкости, жидкости.
#2#Опыт 1. Убедимся, что чем выше скорость воздуха, тем меньше давление в нем.
Зажжем свечу и через тонкую трубочку, например для коктейля, сильно дунем в нее так, чтобы струйка воздуха прошла примерно на расстоянии 2 см от пламени. Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.
Пламя свечи отклонится по направлению к трубочке, хотя на первый взгляд кажется, что воздух должен если и не задуть его, то по крайней мере отклонить в противоположную сторону.
Почему? Согласно уравнению Бернулли, чем выше скорость потока, тем меньше давление в нем. Воздух выходит из трубочки с большой скоростью, так что давление в струе воздуха меньше, чем в окружающем свечу неподвижном воздухе. Перепад давления при этом направлен в сторону выходящего из трубочки воздуха, что и отклоняет к ней пламя свечи.
#4# Принцип работы пульверизатора: атмосферное давление выжимает жидкость в струю воздуха, где давление ниже.На этом принципе работают пульверизаторы, струйные насосы и автомобильные карбюраторы: жидкость втягивается в поток воздуха, давление в котором ниже атмосферного.
Опыт 2. Возьмем лист писчей бумаги за верхние края, поднесем его к стене и удержим на расстоянии примерно 3-5 см от стены.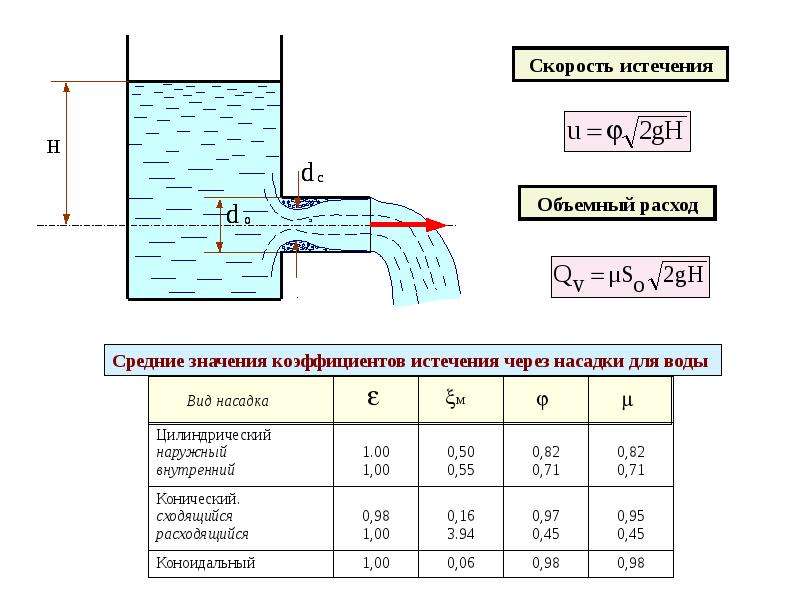 Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.
Подуем в промежуток между стеной и листом. Вместо того, чтобы отклониться от стенки, лист прижимается к ней за счет силы, которую может создавать только возникший перепад давления, направленный к стене. Значит, давление в струе воздуха между листом и стеной меньше, чем в неподвижном воздухе снаружи. Чем сильнее дуть в промежуток, тем плотнее будет прижиматься листок к стене.
Уравнение Бернулли объясняет также классический опыт с трубой переменного сечения. В силу закона неразрывности для сохранения потока массы жидкости в суженной части трубы ее скорость должна быть выше, чем в широкой. Следовательно, давление выше там, где труба шире, и ниже там, где она уже. На этом принципе работает устройство для измерения скорости или расхода жидкости — трубка Вентури.
Падение внутреннего давления в потоке — хорошо проверенный экспериментальный факт, тем не менее он, вообще говоря, парадоксален. Действительно, интуитивно ясно, что жидкость, «протискиваясь» из широкой части трубы в узкую, «сжимается», а это должно привести к росту давления в ней. Такому поведению жидкости в настоящее время нет объяснения даже на молекулярном уровне, по крайней мере, автор его нигде не обнаружил.
Такому поведению жидкости в настоящее время нет объяснения даже на молекулярном уровне, по крайней мере, автор его нигде не обнаружил.
Существование сопротивления среды было обнаружено еще Леонардо да Винчи в XV столетии. Мысль, что сопротивление жидкости движению тела пропорционально скорости тела, впервые высказал английский ученый Дж. Уиллис. Ньютон во втором издании своей знаменитой книги «Математические начала натуральной философии» установил, что сопротивление состоит из двух членов, одного — пропорционального квадрату скорости и другого — пропорционального скорости. Там же Ньютон сформулировал теорему о пропорциональности сопротивления максимальной площади сечения тела, перпендикулярного направлению потока. Силу сопротивления тела, медленно движущегося в вязкой жидкости, рассчитал в 1851 году Дж. Стокс. Она оказалась пропорциональной коэффициенту вязкости жидкости, первой степени скорости тела и его линейным размерам.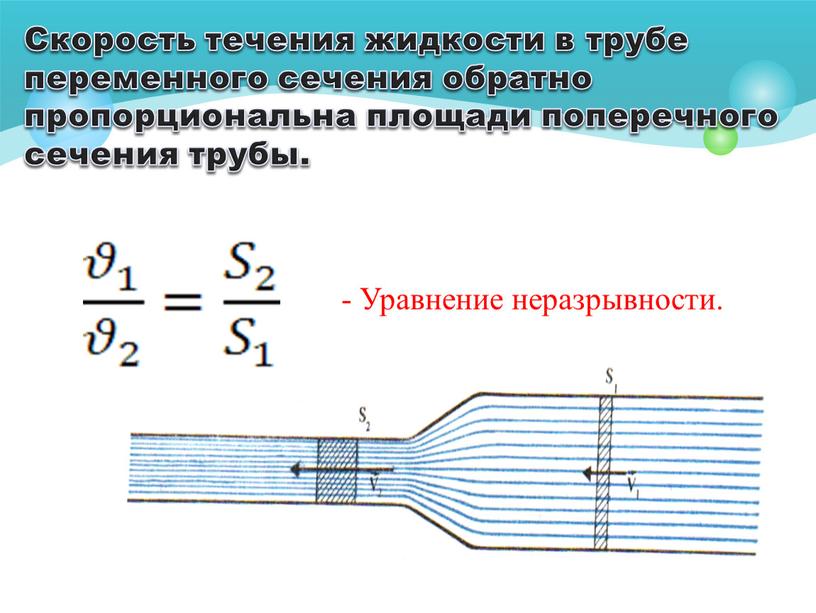
Необходимо отметить, что сопротивление жидкости движущемуся в нем телу в значительной мере обусловливается именно наличием вязкости. В идеальной жидкости, в которой вязкость отсутствует, сопротивление вообще не возникает.
Опыт 1. Посмотрим, как возникает сопротивление движущегося в жидкости тела. Хотя в опыте тело неподвижно, а движется воздух, результата это не меняет. Какая разница, что движется — тело в воздухе или воздух относительно неподвижного тела?
#7#Возьмем свечу и коробок спичек. Зажжем свечу, поставим перед ней на расстоянии примерно 3 см коробок и сильно дунем на него. Пламя свечи отклоняется к коробку. Это означает, что позади коробка давление стало меньше, чем позади свечи, и разность давлений направлена по движению потока воздуха. Следовательно, тело при движении в воздухе или жидкости испытывает торможение.
Поток воздуха набегает на переднюю поверхность коробка, огибает его по краям и не смыкается позади, а отрывается от препятствия. Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен. Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.
Поскольку давление воздуха меньше там, где его скорость выше, давление по краям коробка меньше, чем позади него, где воздух неподвижен. Позади коробка возникает разность давлений, направленная от центра к его краям. В результате воздух за коробком устремляется к его краям, образуя завихрения, что и приводит к уменьшению давления.
Сопротивление зависит от скорости движения тела в жидкости, свойств жидкости, формы тела и его размеров. Важную роль в создании сопротивления играет форма задней стороны движущегося тела. Позади плоского тела возникает пониженное давление, поэтому сопротивление можно уменьшить, предотвратив срыв потока. Для этого телу придают обтекаемую форму. Поток плавно огибает тело и смыкается непосредственно за ним, не создавая области пониженного давления.
Опыт 2. Чтобы продемонстрировать различный характер обтекания, а следовательно, и сопротивле ния тел различной формы, возьмем шар, например мяч для пинг-понга или тенниса, приклеим к нему бумажный конус и поставим за ним горящую свечу.
Повернем тело шариком к себе и подуем на него. Пламя отклонится от тела. Теперь повернем тело к себе острым концом и снова подуем. Пламя отклоняется к телу. Этот опыт показывает, что форма задней поверхности тела определяет направление перепада давления позади нее, а следовательно , и сопротивление тела в потоке воздуха.
В первом опыте пламя отклоняется от тела; это означает, что перепад давления направлен по потоку. Струя воздуха плавно обтекает тело, смыкается за ним и далее движется обычной струей, которая отклоняет пламя свечи назад и может даже задуть его. Во втором опыте пламя отклоняется к телу — как и в эксперименте с коробком, позади тела создается разрежение, перепад давления направлен против потока. Следовательно, в первом опыте сопротивление тела меньше, чем во втором.
ПАДЕНИЕ ДАВЛЕНИЯ В ВЯЗКОЙ ЖИДКОСТИ ПРИ ЕЕ ДВИЖЕНИИ В ТРУБЕ ПОСТОЯННОГО СЕЧЕНИЯОпыт показывает, что давление в жидкости, текущей по трубе постоянного сечения, падает вдоль трубы по течению: чем дальше от начала трубы, тем оно ниже. Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.
Чем уже труба, тем сильнее падает давление. Это объясняется наличием вязкой силы трения между потоком жидкости и стенками трубы.
Опыт. Возьмем резиновую или пластиковую трубку постоянного сечения и такого диаметра, чтобы ее можно было насадить на носик водопроводного крана. Сделаем в трубке два отверстия и откроем воду. Из отверстий начнут бить фонтанчики, причем высота ближнего к крану фонтанчика будет заметно выше, чем расположенного дальше по потоку. Это показывает, что давление воды в ближайшем к крану отверстии выше, чем в дальнем: оно падает вдоль трубы в направлении потока.
#9#Объяснение этого явления на молекулярном уровне автору не известно. Поэтому приведем классическое объяснение. Выделим в жидкости маленький объем, ограниченный стенками трубки и двумя сечениями слева и справа. Так как жидкость течет по трубке равномерно, то разность давлений слева и справа от выделенного объема должна быть уравновешена силами трения между жидкостью и стенками трубки.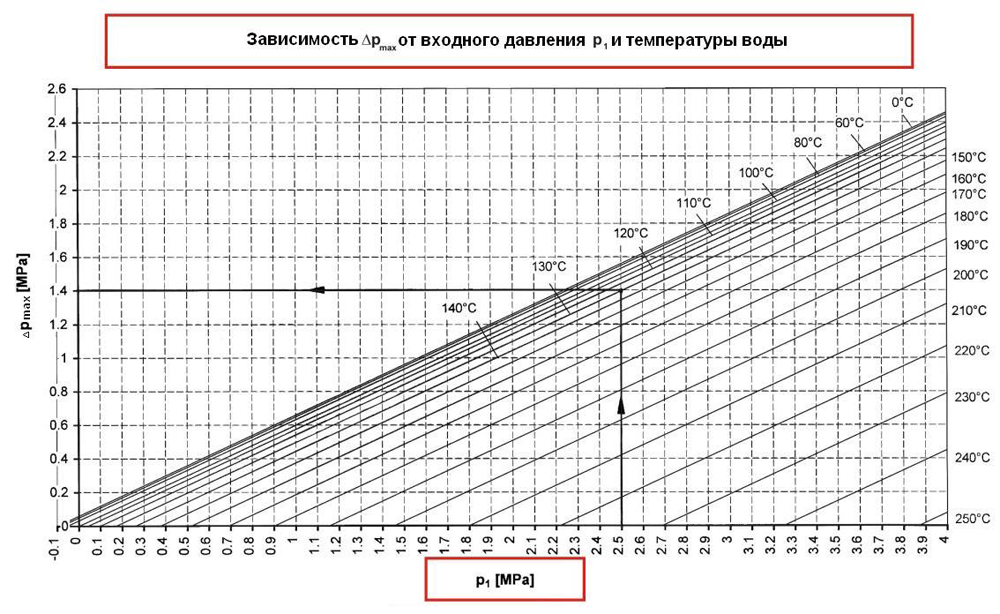 Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.
Следовательно, давление справа, в направлении потока жидкости, будет меньше давления слева. Отсюда заключаем, что давление жидкости уменьшается в направлении течения воды.
На первый взгляд приведенное объяснение удовлетворительно. Однако возникают вопросы, ответа на которые пока нет.
1. Согласно уравнению Бернулли, уменьшение давления в жидкости при ее движении вдоль трубы должно означать, что скорость ее, наоборот, должна расти вдоль потока, то есть течение жидкости должно ускоряться. Но этого не может быть в силу закона неразрывности.
2. Силы трения между стенками трубы и жидкостью должны в принципе тормозить ее. Если это так, то при торможении скорость жидкости вдоль канала должна падать, что в свою очередь приведет к росту давления в ней по потоку. Однако внешнее давление, прокачивающее жидкость по трубе, компенсирует силы трения, заставляя жидкость течь равномерно с одинаковой по всему каналу скоростью. А раз так, то и давление жидкости вдоль канала должно быть везде одинаковым.
Итак, налицо экспериментальный факт, который легко проверить, однако объяснение его остается открытым.
ЭФФЕКТ МАГНУСАРечь идет о возникновении силы, перпендикулярной потоку жидкости при обтекании ею вращающегося тела. Этот эффект был обнаружен и объяснен Г. Г. Магнусом (около середины XIX столетия) при изучении полета вращающихся артиллерийских снарядов и их отклонения от цели. Эффект Магнуса состоит в следующем. При вращении летящего тела близлежащие слои жидкости (воздуха) увлекаются им и также получают вращение вокруг тела, то есть начинают циркулировать вокруг него. Встречный поток рассекается телом на две части. Одна часть направлена в ту же сторону, что и циркулирующий вокруг тела поток; при этом происходит сложение скоростей набегающего и циркулирующего потоков, значит, давление в этой части потока уменьшается. Другая часть потока направлена в сторону, противоположную циркуляции, и здесь результирующая скорость потока падает, что приводит к увеличению давления. Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).
Разность давлений с обеих сторон вращающегося тела и создает силу, которая перпендикулярна к направлению встречного, набегающего потока жидкости (воздуха).
Опыт. Склеим из листа плотной бумаги цилиндр. Из доски, положенной одним краем на стопку книг, сделаем на столе наклонную плоскость и положим на нее цилиндр. Скатившись, он вроде бы должен дальше двигаться по параболе и упасть дальше от края. Однако вопреки ожидаемому траектория его движения загибается в другую сторону, и цилиндр залетает под стол. Все дело в том, что он не просто падает, а еще и вращается, создавая вокруг себя циркуляцию воздуха. Возникает избыточное давление, направленное в сторону, противоположную поступательному движению цилиндра.
#11#Эффект Магнуса позволяет игрокам в пинг-понг и теннис отбивать «крученые» мячи, а футболистам — посылать «сухой лист», ударяя мяч по краю.
ЛАМИНАРНЫЙ И ТУРБУЛЕНТНЫЙ ПОТОКИОпыт обнаруживает две совершенно разные картины движения жидкости. При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.
При низких скоростях наблюдается спокойное, слоистое течение, которое называется ламинарным. При больших скоростях течение становится хаотическим, частицы и отдельные области жидкости движутся беспорядочно, закручиваясь в вихри; такое течение называется турбулентным. Переход от ламинарного течения к турбулентному и обратно осуществляется при определенной скорости жидкости и зависит также от вязкости и плотности жидкости и характерного размера обтекаемого жидкостью тела. До сих пор не ясно, возникают ли вихри с самого начала и имеют просто очень малые размеры, не видимые нами, или вихри возникают начиная с некоторой скорости движения жидкости.
Опыт. Посмотрим, как происходит переход ламинарного потока в турбулентный. Откроем кран и пустим воду сначала тоненькой струйкой, а потом все сильнее и сильнее (конечно, так, чтобы не затопить соседей). Тоненькая струйка движется плавно и спокойно. По мере того, как увеличивается напор воды, скорость струи растет, и, начиная с некоторого момента, вода в ней начинает закручиваться — возникают вихри. Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение — оно становится турбулентным.
Появляясь сначала только в ограниченной области струи, с ростом напора вихри в конце концов охватывают все течение — оно становится турбулентным.
Оценить скорость течения жидкости или газа, при которой возникает турбулентность, можно при помощи так называемого числа Рейнольдса Re = ρvl/μ, где ρ — плотность жидкости или газа, μ — их вязкость (вязкость воздуха, например, 18,5.10-6 Па.с; воды — 8,2.10-2 Па.с), v — скорость потока, l — характерный линейный размер (диаметр трубы, длина обтекаемого тела и пр.). Для каждого вида течений существует такая критическая величина Reкр, что при Re<Reкр возможно только ламинарное течение, а при Re>Reкр оно может стать турбулентым. Если измерить скорость течения воды из крана или вдоль желоба, то, исходя из приведенных значений, можно самим определить, при каком значении Reкр в потоке начинает развиваться турбулентность. Оно должно быть порядка 2000.
Если измерить скорость течения воды из крана или вдоль желоба, то, исходя из приведенных значений, можно самим определить, при каком значении Reкр в потоке начинает развиваться турбулентность. Оно должно быть порядка 2000.
75. Гидравлика: Понятие потерь давления
| 75. Гидравлика: Понятие потерь давления |
Напомним, что этот вопрос вкратце уже упоминался в разделе 18 «Проблема внезапного вскипания хладагента в жидкостной магистрали «. Чтобы пополнить наши знания в этой области, проведем небольшой мысленный опыт с помощью схем на рис. 75.1 и 75.2. Для проведения этого опыта нам потребуются ручной кран на сливной магистрали градирни, при открытии которого градирня опорожняется, и поплавковый клапан, поддерживающий постоянный уровень воды в баке градирни. На выходе из сливной магистрали в точке В (перед краном) установим манометр, проградуированный в барах. Этот манометр будет показывать нам давление в точке В. Установим также стеклянную трубку, которая будет показывать давление в точке В в метрах водяного столба (м вод. ст.), то есть высоту уровня воды, эквивалентную давлению в точке В.
Установим также стеклянную трубку, которая будет показывать давление в точке В в метрах водяного столба (м вод. ст.), то есть высоту уровня воды, эквивалентную давлению в точке В.
На рис. 75.1 слева {схема 1) кран на сливной магистрали закрыт. Уровень воды в трубке находится на высоте 5 м, то есть давление в точке В равно 5 м вод. ст. Манометр в точке В показывает величину избыточного давления, обусловленного высо-
той столба жидкости, то есть 5 м вод. ст. или 0,5 бар: давление, измеренное манометром, равно высоте столба.
На рис. 75.1 справа (схема 2) кран на сливной магистрали открыт. Под действием силы тяжести, сразу же после открытия крана, вода из бака начинает сливаться. Как только вода приходит в движение, ее уровень в стеклянной трубке падает до 4,5 м: следовательно, потери давления на участке от точки А до точки В равны 5 — 4,5 = 0,5 м вод. ст. Манометр в точке В также показывает падение давления на величину потерь, которые равны 0,5 — 0,45 = 0,05 бар (то есть 0,5 м вод. ст.).
ст.).
Отсюда делаем вывод: как только вода пришла в движение, появились потери давления.
Эти потери обусловлены вязкостью воды и за-висят от ее скорости. В основном, потери давления определяются силой трения движущейся воды о внутреннюю поверхность стенок трубопровода, которая имеет ту или иную шероховатость.
Потери давления растут:
► с ростом длины трубы;
► с падением внутреннего диаметра (площади проходного сечения) трубы;
► с ростом скорости воды (то есть расхода) в трубе.
Потери давления приводят к дополнительным затратам энергии. Они порождают шумы в трубопроводах и незначительный нагрев воды. Чем больше скорость воды, тем больше шум, особенно там, где поток испытывает сужения. Например, в кранах, вентилях и т.п. Этот шум может доставлять определенные неудобства в тех случаях, когда трубопроводы проложены в жилых помещениях или поблизости от них.
Поэтому диаметры трубопроводов должны выбираться таким образом, чтобы скорость жидкости в них не превышала определенных значений при максимальных потребных расходах.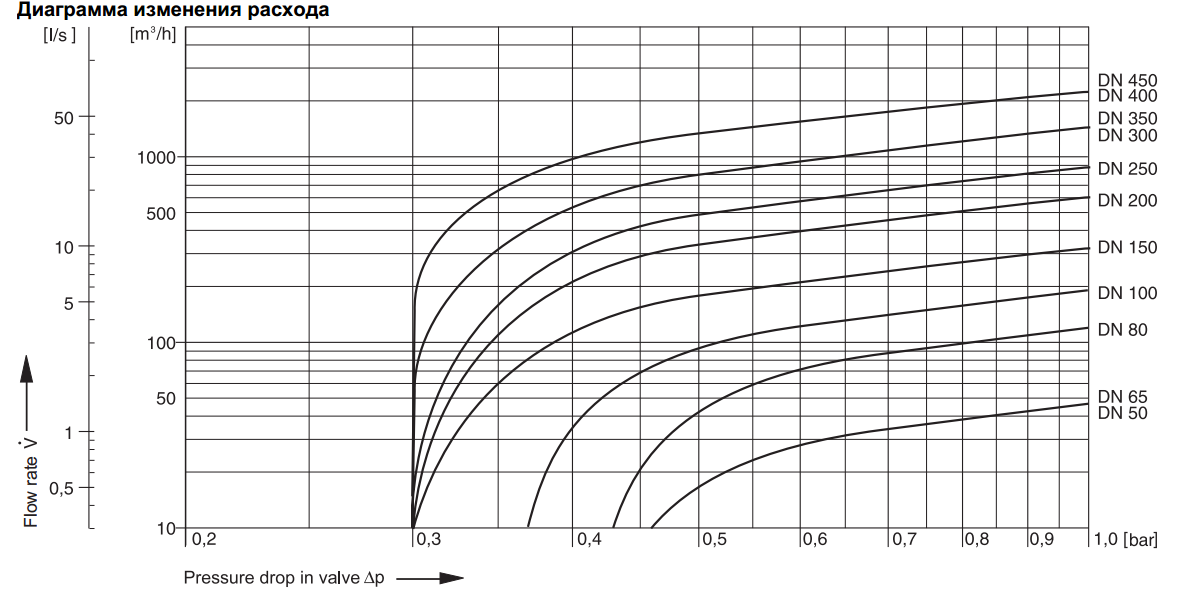 Например, сегодня существуют такие рекомендации:
Например, сегодня существуют такие рекомендации:
► Для труб с внутренним диаметром 15 мм максимальная скорость жидкости равна 0,5 м/с.
► Для труб с внутренним диаметром 80 мм максимальная скорость жидкости равна 1,2 м/с.
Такая разница в рекомендуемых значениях скоростей обусловлена следующим
В трубах диаметром 15 мм периметр поверхности трения П=1,5смх7г«5 см, площадь проходного сечения S1 « 2 см2, а в трубах диаметром 80 мм периметр поверхности трения П = 8 см х п к 25 см при площади проходного сечения S2 * 50
Таким образом, при переходе от трубы с внутренним диаметром D1 = 15 мм к трубе с диаметром D2 = 80 мм
периметр поверхности трения возрастает в 5 раз, тогда как площадь проходного сечения увеличивается в 25 раз. В результате сила трения (а следовательно, и потери давления) в трубе диаметром 15 мм при скорости потока 0,5 м/с будет примерно такой же, как и в трубе диаметром 80 мм при скорости потока 1,2 м/с. Поэтому чем больше диаметр трубы, тем больше в ней может быть скорость потока при одной и той же величине потерь давления на трение.
В существующих сегодня установках диаметры жидкостных трубопроводов выбирают с таким расчетом, чтобы при максимальном расходе скорость потока в них приводила бы к потерям давления, как правило, в диапазоне от 10 до 20 мм вод. ст. на погонный метр длины трубопровода.
| 75.1. УПРАЖНЕНИЕ 1. Оценка потерь давления |
Для оценки потерь давления, обусловленных местными сопротивлениями (повороты, тройники, запорные вентили и т.д.), принято использовать понятие эквивалентной длины. Например, можно считать, что потери давления при повороте потока на 90° эквивалентны потерям давления на трение на отрезке трубы того же диаметра длиной 0,8 м*.
Теперь попробуйте оценить порядок величины потерь давления в трубе внутренним диаметром 65 мм и полной длиной 50 м, имеющей 6 поворотов на 90° (см. рис. 75.4).
Решение упражнения 1
При условии, что диаметр трубы определен правильно, можно предположить, что потери давления на трение составляют от 10 до 20 мм вод. ст. на погонный метр длины трубы. При выполнении оценки допустим, что потери давления на трение равны среднему значению указанного диапазона, то есть 15 мм вод. ст./м. В тоже время, 6 поворотов на 90° эквивалентны по величине потерь давления участку прямой трубы того же диаметра длиной 6 х 0,8 м = 4,8 м. Следовательно, полная эквивалентная длина нашей трубы будет равна 50 м + 4,8 м « 55 м. Таким образом, полные потери давления в этой трубе составят 55 м х 15 мм вод. ст/м = 825 мм вод. ст « 0,8 м вод. ст.
ст. на погонный метр длины трубы. При выполнении оценки допустим, что потери давления на трение равны среднему значению указанного диапазона, то есть 15 мм вод. ст./м. В тоже время, 6 поворотов на 90° эквивалентны по величине потерь давления участку прямой трубы того же диаметра длиной 6 х 0,8 м = 4,8 м. Следовательно, полная эквивалентная длина нашей трубы будет равна 50 м + 4,8 м « 55 м. Таким образом, полные потери давления в этой трубе составят 55 м х 15 мм вод. ст/м = 825 мм вод. ст « 0,8 м вод. ст.
* Это утверждение не всегда справедливо. В общем случае длину участка прямой трубы, эквивалентную по величине потерь давления какому-либо местному сопротивлению, находят по формуле Ьэкв = Щм/Ялтл Т№ D — внутренний диаметр трубы, §м — коэффициент местных потерь и Ятр — коэффициент трения жидкости о внутреннюю поверхность стенок трубы (прим. ред.).
ВЛИЯНИЕ РАЗНОСТИ УРОВНЕЙ НА ПОТЕРИ ДАВЛЕНИЯ
Продолжим наши мысленные эксперименты. На рис. 75.5 представлены две абсолютно одинаковые схемы, отличающиеся только тем, что высота бака градирни на схеме 1 над сливным краном больше, чем высота бака на схеме 2.
Длина сливных труб в обеих схемах одна и та же, диаметры труб также одинаковы. Из-за разности уровней давление в точке В схемы 1 будет выше, чем давление в точке В схемы 2. Следовательно, если полностью открыть сливные краны в обеих схемах, расход Qvl будет выше, чем расход Qv2. Для того, чтобы сравнивать величины потерь давления в зависимости от разности уровней, необходимо прикрыть кран схемы 1 с целью выравнивания расходов, а следовательно, и скоростей потоков жидкости в трубопроводах схем 1 и 2.
Как только мы это сделаем, то сразу же увидим, что при равенстве расходов Qvl и Qv2 потери давления для обеих схем будут в точности совпадать: Ahl = Ah3.
Вывод: потери давления на трение и местные сопротивления никоим образом не зависят от разности уровней трубопровода. Они определяются только расходом жидкости, длиной трубопровода, внутренним диаметром и шероховатостью стенок трубы.
| 75.2. УПРАЖНЕНИЕ 2. Влияние потерь давления на характеристики потока |
Рассмотрим систему, представленную на рис. 75.6.
75.6.
При движении воды по трубопроводу появляются потери давления АЫ, которые зависят от длины трубопровода, его диаметра и расхода воды (то есть скорости воды в трубе).
Установим на выходе из бака фильтр.
► Как изменятся потери давления Ahl?
► Как изменится расход?
► Как изменится скорость воды?
Решение на следующей странице…
Решение упражнения 2
Фильтр, установленный на трубопроводе (см. рис. 75.7 справа), ведет себя точно так же, как любое местное сопротивление (поворот, вентиль и др.): он является дополнительным препятствием потоку жидкости, то есть создает дополнительные потери давления при прохождении воды. Эти потери добавляются к потерям на трение. В результате полные потери давления на участке от точки С до точки В возрастут (Ah3 > Ah 1).
Теперь рассмотрим, как изменится скорость течения воды в трубе. При установке дополнительного сопротивления, например, фильтра, потери давления на отрезке С-В возрастают (Ah3 > Ah 1).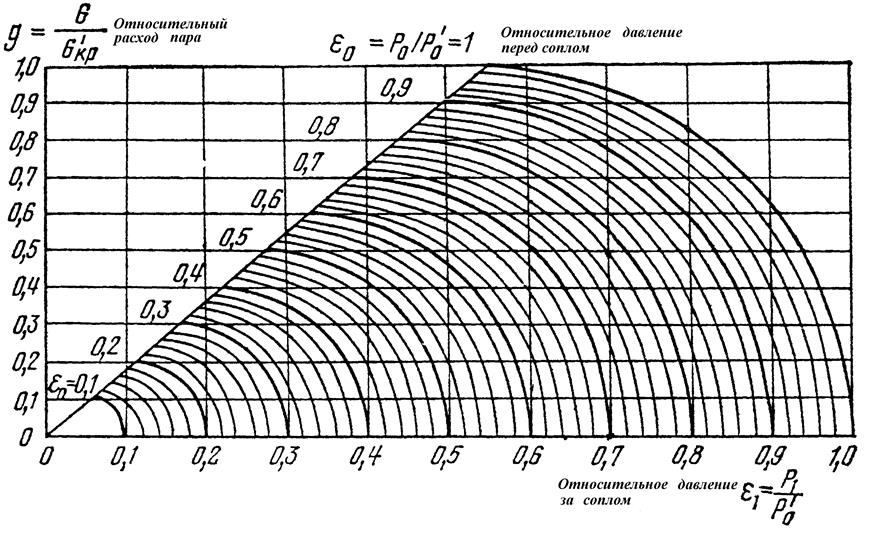 Но это сопротивление также препятствует и прохождению воды (как это делал бы ручной вентиль, сопротивление которого возрастает при его закрытии): следовательно, расход воды будет уменьшаться.
Но это сопротивление также препятствует и прохождению воды (как это делал бы ручной вентиль, сопротивление которого возрастает при его закрытии): следовательно, расход воды будет уменьшаться.
Поскольку при этом в обоих случаях внутренний диаметр трубы на участке С-В не меняется, уменьшение расхода приводит к снижению скорости потока воды в трубе: скорость V2 будет заметно ниже сорости VI.
При росте потерь давления в контуре расход жидкости падает. Поскольку расход падает, неизбежно снижается и скорость потока.
Обратите внимание на дополнительные условия: следует отчетливо понимать, что скорость потока воды абсолютно одинакова на входе в фильтр и на выходе из него. Поскольку внутренний диаметр трубы одинаков по всей длине, скорость будет в точности одна и та же в каждом сечении трубы.
Скорость потока жидкости при постоянном расходе строго одна и та же в каждом сечении трубы постоянного внутреннего диаметра.
| 75.3. УПРАЖНЕНИЕ 3. Изменение расхода при изменении скорости |
По трубе длиной 50 м с внутренним диаметром 80 мм вода течет со скоростью 1 м/с. Как по-вашему, что произойдет с расходом, если скорость удвоится?
Как по-вашему, что произойдет с расходом, если скорость удвоится?
Решение на следующей странице…
Решение упражнения 3
Мы нарушим традицию, которая действует в нашем руководстве, поскольку здесь мы вынуждены привести несложные формулы и выполнить очень простые расчеты. Пожалуйста, извините нас за это, но вопросы гидравлики довольно сложны и иногда вам могут потребоваться отдельные базовые понятия для того, чтобы разобраться в некоторых явлениях, которые, тем не менее, мы будем стараться объяснять как можно проще.
Для начала вы должны вспомнить, что объемный расход, как правило, измеряется в м3/ч или м3/с (см. раздел 41 «Измерение расхода воздуха»}.
Скорость потока и расход воды находятся в тесной взаимосвязи:
Qv V х S
(м3/с) = (м/с) х (м2)
Расход = Скорость х Площадь
Рассчитаем площадь проходного сечения трубы диаметром 80 мм (см. рис. 75.9): Рис. 75.9. S = 3,14 х 0,082 / 4 = 0,005 м2.
75.9. S = 3,14 х 0,082 / 4 = 0,005 м2.
Теперь можно найти расходы:
► Qvl = 1 м/с х 0,005 м2 = 0,005 м3/с = 0,005 х 3600 = 18 м3/ч.
► Qv2 = 2 м/с х 0,005 м2 = 0,01 м3/с = 0,01 х 3600 = 36 м3/ч.
Таким образом, для данного диаметра трубы расход прямо пропорционален скорости потока.
При удвоении скорости потока жидкости в трубе расход также удваивается.
| 75.4. УПРАЖНЕНИЕ 4. Изменение расхода при изменении диаметра трубы |
Мы только что нашли, что при скорости потока жидкости 1 м/с в трубе диаметром 80 мм расход жидкости равен 18 м3/ч.
Теперь удвоим внутренний диаметр трубы, то есть возьмем трубу с внутренним диаметром 160 мм. Чему будет равен расход жидкости в этой трубе при той же скорости потока
Решение упражнения 4
При скорости потока 1 м/с расход в трубе с внутренним диаметром 80 мм равен 18 м3/ч. Если внутренний диаметр трубы будет равен 160 мм, то площадь ее проходного сечения станет S = 3,14 х 0,1 б2 / 4 = 0,02 м2. При скорости потока 1 м/с расход в этой трубе будет равен 1 х 0,02 = 0,02 м3/с или 0,02 х 3600 = 72 м3/ч вместо прежних 18 м3/ч. Иначе говоря, расход вырастет в 4 раза.
При скорости потока 1 м/с расход в этой трубе будет равен 1 х 0,02 = 0,02 м3/с или 0,02 х 3600 = 72 м3/ч вместо прежних 18 м3/ч. Иначе говоря, расход вырастет в 4 раза.
Внимание! Не путайте понятие «внутренний диаметр » и площадь проходного сечения: если диаметр удваивается, то площадь проходного сечения увеличивается в 4 раза!
СООТНОШЕНИЕ МЕЖДУ РАСХОДОМ И ДАВЛЕНИЕМ
Рассмотрим поплавковый клапан, предназначенный для подачи водопроводной воды в бак градирни (см. рис. 75.11). Допустим, что полностью открытый клапан при давлении воды в сети 2 бара обеспечивает расход 10 л/мин.
Для того, чтобы удвоить расход, то есть обеспечить расход через клапан, равный 20 л/мин. необходимо давление воды в сети увеличить в 4 раза.
Запомните! При слабом давлении воды в водопроводной сети расход будет небольшим. Чтобы удвоить расход, давление в сети нужно повысить в 4 раза.
Разумеется, что на практике для удвоения расхода так не поступают. Если бы на самом деле повышали давление в сети, это породило бы многие проблемы: диаметр трубопровода пришлось бы делать очень малым, вода бы в трубах сильно «гудела» и т.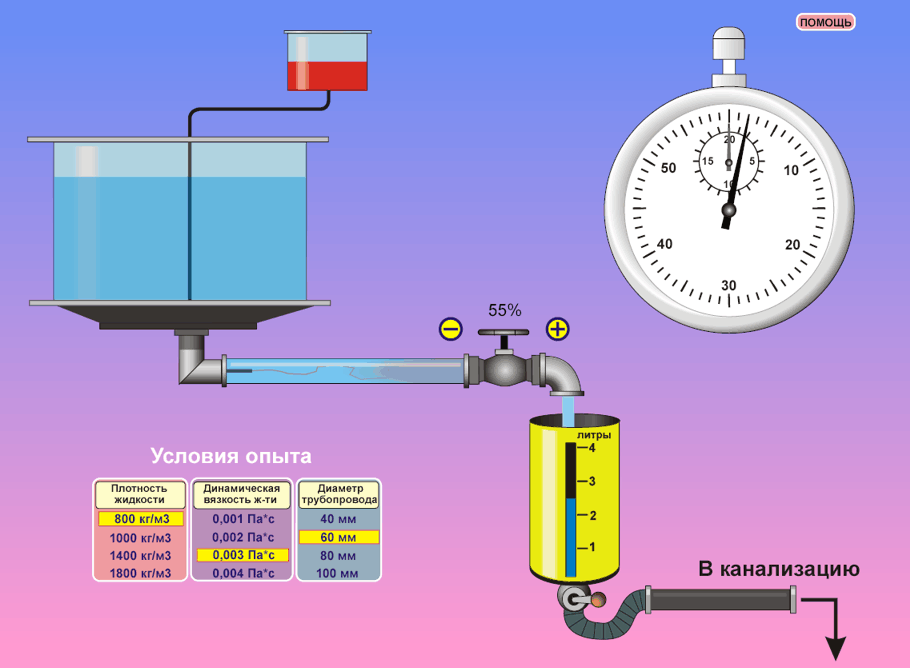 д.
д.
Проведем такую аналогию: если автомагистраль загружена, то для того, чтобы повысить ее пропускную способность, водителей не заставляют ехать быстрее, а либо делают новую полосу, либо строят объездной путь! То же самое предпринимают и для увеличения расхода жидкости в трубе: увеличивают площадь проходного сечения трубы.
При заданном расходе это приводит к снижению скорости потока воды в трубе (и, следовательно, шума), а потребное для обеспечения этого расхода давление уменьшается
СООТНОШЕНИЕ МЕЖДУ РАСХОДОМ И ПОТЕРЯМИ ДАВЛЕНИЯ
В трубе с внутренним диаметром 80 мм предполагается удвоить расход. Что произойдет с потерями давления? На первый взгляд может показаться, что поскольку при удвоении расхода скорость потока удваивается, то и потери давления также должны удваиваться. К сожалению, это не так.
При удвоении расхода потери не удваиваются, а увеличиваются в четыре раза: если расход вырос в 2 раза, потери давления возрастут в 4 раза!
В примере на рис. 75.13 при скорости потока 1 м/с потери давления АР = 2 м вод. ст., а при увеличении скорости до 2 м/с потери давления умножаются на 4: АР = 2 х 4
75.13 при скорости потока 1 м/с потери давления АР = 2 м вод. ст., а при увеличении скорости до 2 м/с потери давления умножаются на 4: АР = 2 х 4
Потери давления пропорциональны квадрату расхода.
Для получения дополнительной информации см. раздел 95 «Несколько примеров расчета потерь давления «.
| 75.5. УПРАЖНЕНИЕ 5. Изменение потерь давления при изменении расхода |
Показан участок трубопровода, пропускающий воду со скоростью I м/с. Манометры показывают давление в различных точках этого трубопровода. Из показаний манометров можно сделать следующие выводы.
При скорости водяного потока 1 м/с потери давления составляют:
— на фильтре АРф = 2 — 1,8 = 0,2 бар;
— на вентиле АРв = 1,8 — 1,7 = 0,1 бар.
Что покажут манометры на выходе из фильтра и на выходе из вентиля, если скорость потока в трубе удвоится? Решение этого упражнения приведено ниже, однако прежде, чем знакомиться с ним, попробуйте поразмышлять самостоятельно.
Решение упражнения 5
Скорость удвоилась, следовательно расход тоже удвоился. В результате потери давления на
фильтре и на вентиле вырастут в 4 раза.
Теперь потери давления на фильтре АРф = 0,2 бар х 4 = 0,8 бар, то есть манометр на выходе
из фильтра покажет 2 — 0,8 =1,2 бар.
Потери давления на вентиле АРв = 0,1 бар х 4 = 0,4 бар, то есть манометр на выходе из
вентиля покажет 1,2 — 0,4 = 0,8 бар.
Заметьте, что общие потери давления на этом участке вырастут с 0,3 до 1,2 бар: то есть тоже в 4 раза.
Гидроудар в трубе — причины, защита, компенсаторы
Защита от гидроудара
Чтобы защитить трубопровод от гидравлических ударов, нужно:
- Плавно открывать/закрывать запорные элементы
При плавном закрывании крана давление в трубопроводе будет постепенно выравниваться. При этом ударная волна будет иметь незначительную силу, а следовательно, мощность гидравлического удара будет минимальной. Но не во всех случаях возможно обеспечить плавное закрывание крана. Далеко не у всех моделей вентильная конструкция, многие современные краны имеют шаровую систему – достаточно одного неосторожного резкого поворота и кран придёт в положение «закрыто».
Но не во всех случаях возможно обеспечить плавное закрывание крана. Далеко не у всех моделей вентильная конструкция, многие современные краны имеют шаровую систему – достаточно одного неосторожного резкого поворота и кран придёт в положение «закрыто».
- Использовать трубы большого диаметра
В трубопроводах большого диаметра рабочая среда движется с меньшей скоростью, чем в системах с более маленьким диаметром. А чем скорость перемещения потока жидкости меньше, тем слабее сила гидроудара. Однако данный способ гораздо затратнее. Расходы увеличиваются за счёт более высокой стоимости труб и теплоизоляции.
- Установить амортизирующее устройство
Данное устройство располагается по направлению движения рабочей жидкости. В качестве амортизатора используется отрезок трубы из эластичного пластик либо каучука, которым заменяется часть жёсткой трубы перед термостатом. При возникновении гидравлического удара происходит растяжение эластичного отрезка и частичное гашение силы удара.
- Использовать компенсаторное оборудование
Для сбрасывания лишней жидкости до момента нормализации давления в трубопроводе используется гидравлический аккумулятор. Данное оборудование выполнено в виде герметичного бака, оснащённого мембраной и воздушным клапаном. Мембрана изготавливается из эластичного материала, бак – из стали.
- Использовать автоматику насосов
Одной из причин появления гидравлических ударов в трубопроводе является насосное оборудование. Движение рабочей среды зависит от того, насколько быстро вращаются насосные валы. Следовательно, плавное снижение/увеличение скорости вращения позволяет уменьшить силу воздействия и снизить риск появления гидроударов.
На производствах для управления насосным оборудованием используются специальные регуляторы, частотные преобразователи и прочие подобные приборы. Данное оборудование также подходит для использования в бытовых условиях.
Гидравлические удары в коммуникациях появляются при остановке насосного оборудования, например, при исчезновении сети питания. На производствах и в сфере коммунального хозяйства резервные источники используются давно и не раз доказали свою эффективность. Предупреждение аварийных ситуаций и сокращение расходов на ремонтные работы приводят к существенной экономии средств. Включение домашнего насосного оборудования через устройство защиты от гидроударов (стабилизаторы и источники резервного питания) поможет обезопасить внутренние коммуникационные системы.
На производствах и в сфере коммунального хозяйства резервные источники используются давно и не раз доказали свою эффективность. Предупреждение аварийных ситуаций и сокращение расходов на ремонтные работы приводят к существенной экономии средств. Включение домашнего насосного оборудования через устройство защиты от гидроударов (стабилизаторы и источники резервного питания) поможет обезопасить внутренние коммуникационные системы.
- Использовать байпас
Байпас представляет собой дополнительный участок трубопровода, который используется в качестве обходного канала и служит для регулирования пропускной способности сети отопления. Такие устройства можно монтировать, как в новые системы, так и в уже существующие.
- Гаситель гидроударов
Это простое, но эффективное изобретение, работающее по принципу расширительного бака отопительных коммуникаций. При резком перепаде давления жидкость перемещается в мембранный гаситель. После того, как давление в трубопроводе упадёт до рабочей величины, произойдёт выталкивание жидкости обратно в систему. Возвращение воды обеспечивается благодаря избыточному давлению воздуха, находящегося с противоположной стороны мембраны.
Возвращение воды обеспечивается благодаря избыточному давлению воздуха, находящегося с противоположной стороны мембраны.
- Защитный клапан
Клапан защиты от гидроудара располагается в трубопроводной системе рядом с наносом. Он реагирует на скачки давления, принимая обратную волну и предотвращая гидравлические удары. Клапан оснащён специальным регулятором, который при перепаде давления плавно открывает его. Таким образом, когда обратный поток рабочей среды доходит до насосного агрегата, клапан уже находится в открытом состоянии. В результате этого происходит сбрасывание воды, а следовательно, снижение давления до допустимой величины. После нормализации давления регулятор закрывает клапан, чтобы предотвратить опустошение системы.
Выбор диаметра трубы в зависимости от расхода воды онлайн калькулятор таблица
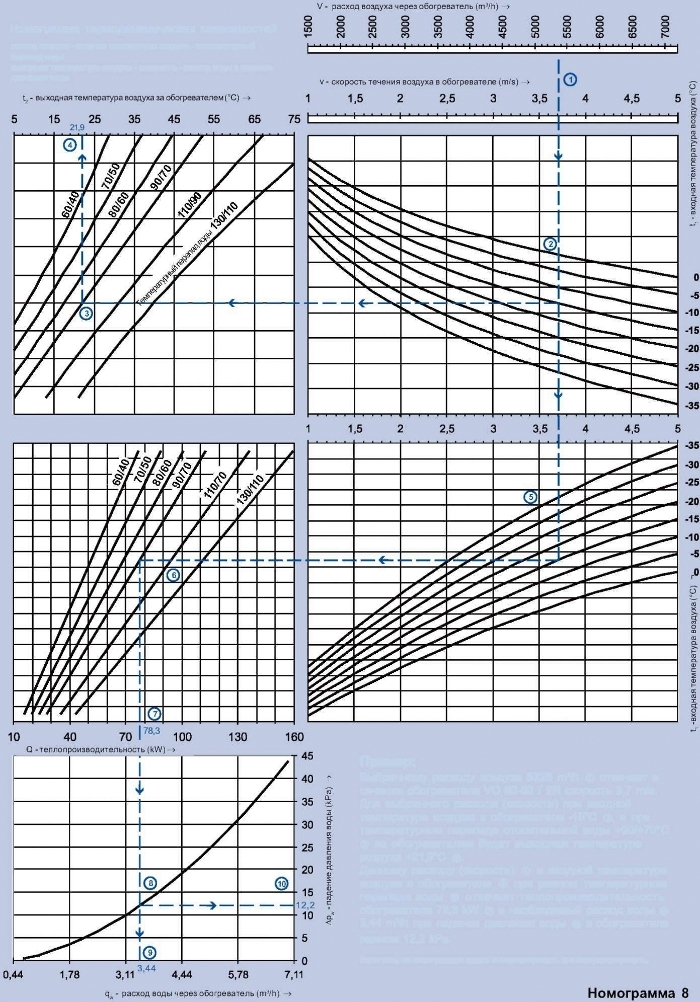
Таблица выбора диаметра трубы от расхода воды
| Диаметр, дюйм |
Диаметр, мм |
Расход воды м3/час |
| 1″ |
25. 4 4 |
1.8 |
| 1 1/4″ |
32 |
3.3 |
| 1 1/2″ |
38.1 |
5.1 |
| 2″ |
50.8 |
10.7 |
| 2 1/2″ | 63. 5 5 |
19.1 |
| 3″ |
76 |
30.4 |
| 3 1/2″ | 89 |
45.6 |
| 4″ |
102 |
64.9 |
| 4 1/2 | 114 |
86. 4 4 |
Расчет расхода воды в зависимости от диаметра трубы. Не целые числа вводите через точку (АА.АА)
Значения величин в этой таблице основаны на принятых в практике соответствиях диаметров труб расходам воды. Эти практические расчеты основаны на том требовании, что скорость воды в трубах не должна достигать шумового предела (приблизительно 2 метра в секунду для труб диаметром до 50 мм и 3 метра в секунду для труб диаметром до 114 мм), и обычно она оказывается в диапазоне 0.8-1.5 м/c для труб диаметром до 50 мм и до 2.5 метров в секунду для труб диаметром до 114 мм, в бетонном производстве трубы большего диаметра для подачи воды практически не используются. Поэтому вычисления по этой таблице допустимы только до диаметра 114 мм. Для труб большего диаметра данные мы не собирали и не анализировали.
Еще раз обращаем внимание — расчеты на данной странице можно вести только для труб диаметром до 114 мм.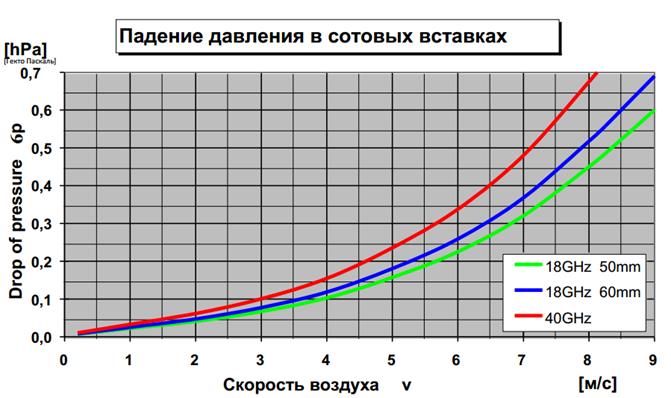 !!!
!!!
При выборе диаметра трубы нужно учесть непостоянный характер потребления!
К примеру : необходимо для производства 30 м3 бетона 4.5 тонн воды и 2 тонны для заправки миксеров, итого 6.5 тонн воды. Казалось бы, по таблице можно выбрать с запасом трубу диаметром 50 мм. с расходом 10.7 тонны воды в час. Это неправильный ответ. Вода для приготовления бетона будет потребляться не час, а 20-30 минут, остальное время — выгрузка бетона, технологические простои. Поэтому труба должна пропускать не 4.5, а 9-13.5 тонн воды для приготовления бетона. Ну и плюс 2 тонны для миксеров. Итого не 6.5, а 11-15.5 тонн воды. Нужно выбирать 53-ю или 57-ю трубу. Кстати, все вышесказанное относится и к выбору насосов.
Компания Тех Альянс не несет ответственности за любые последствия, наступившие при использовании результатов данных расчетов.
Закон Бернулли : Помогите решить / разобраться (Ф)
Скорость потока частично гасится на заслонке.
Если сечение трубы остаётся после крана тем же самым, то и скорость потока после крана неизменно будет равна скорости потока до крана. Потому что поток воды сохраняется. А гасится не скорость, а энергия, переносимая потоком воды в трубе в единицу времени, и, соответственно, давление. До крана поток энергии в трубе оказывается выше, чем после крана.
В сплошной среде, такой, как жидкость, поток энергии связан не только с переносом кинетической или потенциальной энергии частиц среды, но часть потока энергии также связана с работой сил давления при перемещении среды. Рассмотрите немного другой пример из механики. Вы поднимаете тяжелое ведро при помощи верёвки. Скорость ведра постоянна, его кинетическая энергия не изменяется. Но ведро поднимается вверх, значит, его потенциальная энергия возрастает. Откуда берётся эта энергия? Она передаётся ведру от ваших мышц, совершающих работу. Но как она передаётся ведру, если вы тянете только за верёвку? Она передаётся при перемещении натянутой верёвку. И она не связана ни с кинетической, ни с потенциальной энергией верёвки, так как верёвка очень лёгкая. А энергия от ваших мышц передаётся ведру при перемещении этой натянутой верёвки как работа силы натяжения верёвки.
И она не связана ни с кинетической, ни с потенциальной энергией верёвки, так как верёвка очень лёгкая. А энергия от ваших мышц передаётся ведру при перемещении этой натянутой верёвки как работа силы натяжения верёвки.
Точно так же и в трубе. Поток воды, кроме кинетической и потенциальной энергии переносимой воды, также, переносит часть энергии вдоль трубы за счёт работы сил давления. Изначально эта энергия поставляется в трубу насосом, создающим давление. Частично эта энергия расходуется на подъём воды от насоса до уровня потребителя, т. е. вашего крана, частично она расходуется на преодоление вязкостных потерь в трубах. Но всё, что осталось, оно вам не нужно, так как вам из крана нужен спокойный поток воды, который будет течь без разбрызгивания. И избыток переносимой водой в трубе энергии вы гасите в кране, который снижает давление и, следовательно, энергию вытекающей из крана воды до приемлемого для вас уровня.
Уравнение Бернулли — это закон сохранения энергии для потока воды, в котором игнорируются потери. Оно применимо для эжекторов, которые проектируются таким образом, чтобы минимизировать потери энергии в них. Но оно неприменимо для кранов, так как краны — это устройства, которые гасят избыточную энергию потока, попутно регулируя поток вытекающей у потребителя воды.
Оно применимо для эжекторов, которые проектируются таким образом, чтобы минимизировать потери энергии в них. Но оно неприменимо для кранов, так как краны — это устройства, которые гасят избыточную энергию потока, попутно регулируя поток вытекающей у потребителя воды.
аэродинамика — Как давление жидкости изменяется в зависимости от площади в соответствии с уравнением неразрывности и уравнением Бернулли?
Я не согласен с ответом, получившим наибольшее количество голосов от CAGT. Он говорит «Эта область полностью отличается от той, что указана выше» , но это ничего не значит. Упомянутое автором уравнение $ p = {F \ over A} $ действительно выполняется, и в нем нет противоречия или парадокса.
Фактически, уравнение $ p = {F \ over A} $ выполняется не только здесь, но и везде в физике.2 \ более 2} + gz = \ text {constant} $$
Итак, ваша проблема связана с $ p = {F \ over A} $. Что ж, с этим проблем нет. Что на самом деле неверно в вашем мышлении, так это то, что вы не обращаете внимание на уравнение : сила $ F $ тоже изменяется.
Давайте резюмируем, что происходит в вашей ситуации:
- Произошло изменение площади поперечного сечения: $ A_2
- Благодаря сохранению массы , (1) подразумевает $ v_2> v_1 $
- Благодаря Бернулли , (2) подразумевает $ p_2
Хорошо, теперь посмотрим на это.
Темно-синий прямоугольник слева — это то, что мы называем элементом . Как и остальной поток в большей секции, он течет со скоростью $ v_1 $. Он разделен слева и справа гранями с областью $ A_1 $. Обратите внимание, что, поскольку жидкость слева и справа от него имеет давление $ p_1 $, этот элемент сжимается силами $ F_1 = p_1 A_1 $ с каждой стороны.
Теперь перейдем к элементу меньшего участка, который течет быстрее. Его площадь поперечного сечения меньше.Давление слева и справа также меньше. В результате сжимающие его силы, $ F_2 = p_2 A_2 $, также меньше.
Итак, $ p = {F \ over A} $ по-прежнему выполняется. Обновлено 14 декабря 2020 г. Эллисон Боули В физике вы, вероятно, решили проблемы сохранения энергии, связанные с автомобилем на холме и массой на холме. пружина и американские горки в петле. Вода в трубе — тоже проблема сохранения энергии. Фактически, именно так математик Даниэль Бернулли подошел к проблеме в 1700-х годах. Используя уравнение Бернулли, рассчитайте расход воды через трубу в зависимости от давления. Преобразование всех измерений в единицы СИ (согласованная международная система измерений). Решите уравнение Бернулли для получения желаемой скорости, будь то начальная скорость в трубе или конечная скорость на выходе из трубы.2 + pgy_2 где P 1 и P 2 — начальное и конечное давления соответственно, p — плотность воды, v 1 и v 2 — начальная и конечная скорости, соответственно, а y 1 и y 2 — начальная и конечная высоты соответственно. Измерьте каждую высоту от центра трубы. Чтобы найти начальный расход воды, решите v 1 . Вычтите P 1 и p g y 1 с обеих сторон, затем разделите на 0.3) и рассчитайте начальный или конечный расход воды в м / с. Если оба v 1 и v 2 в уравнении Бернулли неизвестны, используйте сохранение массы для замены: v_1 = \ frac {v_2A_2} {A_1} \ text {или} v_2 = \ frac {v_1A_1} {A_2} , где A 1 и A 2 — начальная и конечная площади поперечного сечения соответственно (измеренные в м2 ). Выполните аналогичный расчет, чтобы найти окончательный расход воды. Замените ваши измерения для каждой переменной и вычислите начальный или конечный расход воды в единицах м / с. Обновлено 5 декабря 2020 г. Крис Дезиель Физики и инженеры используют закон Пуазейля для предсказания скорости воды в трубе.Это соотношение основано на предположении, что поток является ламинарным, что является идеализацией, которая больше применима к маленьким капиллярам, чем к водопроводным трубам. Турбулентность почти всегда является фактором в трубах большего размера, так же как и трение, вызванное взаимодействием жидкости со стенками трубы. Эти факторы трудно определить количественно, особенно турбулентность, и закон Пуазейля не всегда дает точное приближение. Однако, если вы поддерживаете постоянное давление, этот закон может дать вам хорошее представление о том, как изменяется скорость потока при изменении размеров трубы. Если вы поддерживаете в водяной системе постоянное давление, вы можете рассчитать значение постоянной K, посмотрев вязкость воды при температуре окружающей среды и выразив ее в единицах, совместимых с вашими измерениями. Поддерживая постоянную длину трубы, теперь у вас есть пропорциональность между четвертой степенью радиуса и скоростью потока, и вы можете рассчитать, как скорость изменится при изменении радиуса. Также можно поддерживать постоянным радиус и изменять длину трубы, хотя для этого потребуется другая константа.Сравнение прогнозируемых и измеренных значений расхода показывает, насколько турбулентность и трение влияют на результаты, и вы можете учесть эту информацию в прогнозных расчетах, чтобы сделать их более точными. К концу этого раздела вы сможете: Да, когда ситуация изменится, $ A $ станет меньше, что само по себе сделало бы $ p $ больше. Однако, как мы видели выше, новый $ F $ тоже меньше старого, что само по себе сделало бы $ p $ меньше. Чистый эффект от $ p_2
Да, когда ситуация изменится, $ A $ станет меньше, что само по себе сделало бы $ p $ больше. Однако, как мы видели выше, новый $ F $ тоже меньше старого, что само по себе сделало бы $ p $ меньше. Чистый эффект от $ p_2 Как рассчитать расход воды через трубу на основе давления
Расчет расхода воды с известной скоростью на одном конце
Преобразование измерений в единицы СИ
 Найдите в Интернете таблицы преобразования и конвертируйте давление в Па, плотность в кг / м 3 , высоту в м и скорость в м / с.
Найдите в Интернете таблицы преобразования и конвертируйте давление в Па, плотность в кг / м 3 , высоту в м и скорость в м / с. Решите уравнение Бернулли
Расчет потока воды с неизвестной скоростью на обоих концах
Использовать сохранение массы
 2}}
2}} Замещающие измерения для каждой переменной
Как рассчитать скорость воды в трубах
 4
4 Сравнение скоростей потока
Вязкость и ламинарный поток; Закон Пуазейля
Цели обучения
Ламинарный поток и вязкость
Когда вы наливаете себе стакан сока, жидкость течет свободно и быстро. Но когда вы поливаете блины сиропом, эта жидкость медленно течет и прилипает к кувшину. Разница заключается в трении жидкости как внутри самой жидкости, так и между жидкостью и окружающей средой. Мы называем это свойство жидкостей вязкостью . Сок имеет низкую вязкость, тогда как сироп имеет высокую вязкость.В предыдущих разделах мы рассматривали идеальные жидкости с небольшой вязкостью или без нее. В этом разделе мы исследуем, какие факторы, включая вязкость, влияют на скорость потока жидкости. Точное определение вязкости основано на ламинарном или нетурбулентном потоке. Прежде чем мы сможем определить вязкость, нам нужно определить ламинарный поток и турбулентный поток. На рисунке 1 показаны оба типа потока. Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются.Турбулентный поток, или турбулентность , характеризуется завихрениями и завихрениями, которые смешивают слои жидкости вместе.
На рисунке 1 показаны оба типа потока. Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются.Турбулентный поток, или турбулентность , характеризуется завихрениями и завихрениями, которые смешивают слои жидкости вместе.
Рис. 1. Дым плавно поднимается на некоторое время, а затем начинает образовывать завихрения и водовороты. Плавный поток называется ламинарным потоком, тогда как завихрения и водовороты типичны для турбулентного потока. Если вы посмотрите на дым (стараясь не дышать на него), вы заметите, что при плавном течении он поднимается быстрее, чем после того, как он становится турбулентным, что означает, что турбулентность оказывает большее сопротивление потоку.(кредит: Creativity103)
На рис. 2 схематически показано, чем отличаются ламинарный и турбулентный потоки. Слои текут без перемешивания, когда поток ламинарный. Когда есть турбулентность, слои перемешиваются, и есть значительные скорости в направлениях, отличных от общего направления потока. Линии, показанные на многих иллюстрациях, представляют собой пути, по которым проходят небольшие объемы жидкости. Эти линии называются . Линии тока плавные и непрерывные, когда поток является ламинарным, но разделяются и перемешиваются, когда поток является турбулентным.У турбулентности есть две основные причины. Во-первых, любое препятствие или острый угол, например, в кране, создает турбулентность, сообщая скорости, перпендикулярные потоку. Во-вторых, высокие скорости вызывают турбулентность. Сопротивление как между соседними слоями жидкости, так и между жидкостью и окружающей средой образует завихрения и водовороты, если скорость достаточно велика. В оставшейся части этого раздела мы сконцентрируемся на ламинарном потоке, оставив некоторые аспекты турбулентности для последующих разделов.
Линии, показанные на многих иллюстрациях, представляют собой пути, по которым проходят небольшие объемы жидкости. Эти линии называются . Линии тока плавные и непрерывные, когда поток является ламинарным, но разделяются и перемешиваются, когда поток является турбулентным.У турбулентности есть две основные причины. Во-первых, любое препятствие или острый угол, например, в кране, создает турбулентность, сообщая скорости, перпендикулярные потоку. Во-вторых, высокие скорости вызывают турбулентность. Сопротивление как между соседними слоями жидкости, так и между жидкостью и окружающей средой образует завихрения и водовороты, если скорость достаточно велика. В оставшейся части этого раздела мы сконцентрируемся на ламинарном потоке, оставив некоторые аспекты турбулентности для последующих разделов.
Рисунок 2.(а) Ламинарное течение происходит послойно без перемешивания. Обратите внимание, что вязкость вызывает сопротивление между слоями, а также с неподвижной поверхностью. (b) Препятствие в судне вызывает турбулентность. Турбулентный поток перемешивает жидкость. Здесь больше взаимодействия, больше нагрева и больше сопротивления, чем в ламинарном потоке.
(b) Препятствие в судне вызывает турбулентность. Турбулентный поток перемешивает жидкость. Здесь больше взаимодействия, больше нагрева и больше сопротивления, чем в ламинарном потоке.
Попробуйте одновременно бросить две палки в текущую реку: одну у края реки, а другую — у середины.Какой из них путешествует быстрее? Почему?
На рис. 3 показано, как измеряется вязкость жидкости. Между двумя параллельными пластинами находится определенная жидкость. Нижняя пластина зафиксирована, а верхняя пластина перемещается вправо, увлекая за собой жидкость. Слой (или пластинка) жидкости, контактирующий с любой пластиной, не перемещается относительно пластины, поэтому верхний слой перемещается со скоростью v , в то время как нижний слой остается в покое. Каждый последующий слой сверху вниз воздействует на слой под ним, пытаясь увлечь его, создавая непрерывное изменение скорости от v до 0, как показано. Необходимо следить за тем, чтобы поток был ламинарным; то есть слои не смешиваются. Движение на Рисунке 3 похоже на непрерывное режущее движение. Жидкости имеют нулевую прочность на сдвиг, но скорость , с которой они сдвигаются, связана с теми же геометрическими факторами A и L , как и деформация сдвига для твердых тел.
Необходимо следить за тем, чтобы поток был ламинарным; то есть слои не смешиваются. Движение на Рисунке 3 похоже на непрерывное режущее движение. Жидкости имеют нулевую прочность на сдвиг, но скорость , с которой они сдвигаются, связана с теми же геометрическими факторами A и L , как и деформация сдвига для твердых тел.
Рис. 3. На графике показан ламинарный поток жидкости между двумя пластинами области A. Нижняя пластина закреплена. Когда верхняя пластина сдвигается вправо, она увлекает за собой жидкость.
Сила F требуется, чтобы верхняя пластина на Рисунке 3 двигалась с постоянной скоростью v , и эксперименты показали, что эта сила зависит от четырех факторов. Во-первых, F прямо пропорционально v (пока скорость не станет настолько высокой, что возникает турбулентность — тогда требуется гораздо большая сила, и она имеет более сложную зависимость от v ). Во-вторых, F пропорционально площади A пластины.Это соотношение кажется разумным, поскольку A прямо пропорционально количеству перемещаемой жидкости. В-третьих, F обратно пропорционально расстоянию между пластинами L . Эти отношения также разумны; L похож на плечо рычага, и чем больше плечо рычага, тем меньше силы требуется. В-четвертых, F прямо пропорционально коэффициенту вязкости , η .Чем больше вязкость, тем больше требуется сила. Эти зависимости объединены в уравнение
Во-вторых, F пропорционально площади A пластины.Это соотношение кажется разумным, поскольку A прямо пропорционально количеству перемещаемой жидкости. В-третьих, F обратно пропорционально расстоянию между пластинами L . Эти отношения также разумны; L похож на плечо рычага, и чем больше плечо рычага, тем меньше силы требуется. В-четвертых, F прямо пропорционально коэффициенту вязкости , η .Чем больше вязкость, тем больше требуется сила. Эти зависимости объединены в уравнение
[латекс] F = \ eta \ frac {{vA}} {L} \\ [/ latex],
, что дает нам рабочее определение вязкости жидкости η . Решение относительно η дает
[латекс] \ eta = \ frac {FL} {vA} \\ [/ latex],
, который определяет вязкость с точки зрения ее измерения. Единица вязкости в системе СИ: Н · м / [(м / с) · м 2 ] = (Н / м 2 ) · с или Па · с. В таблице 1 приведены коэффициенты вязкости для различных жидкостей.
В таблице 1 приведены коэффициенты вязкости для различных жидкостей.
Вязкость варьируется от одной жидкости к другой на несколько порядков. Как и следовало ожидать, вязкость газов намного меньше вязкости жидкостей, и эта вязкость часто зависит от температуры. Вязкость крови можно снизить, употребляя аспирин, что позволяет ему легче циркулировать по телу. (При длительном применении в низких дозах аспирин может помочь предотвратить сердечные приступы и снизить риск свертывания крови.)
| Жидкость | Температура (ºC) | Вязкость η (мПа · с) |
|---|---|---|
| Газы | ||
| Воздух | 0 | 0,0171 |
| 20 | 0,0181 | |
| 40 | 0,0190 | |
| 100 | 0,0218 | |
| Аммиак | 20 | 0. 00974 00974 |
| Двуокись углерода | 20 | 0,0147 |
| Гелий | 20 | 0,0196 |
| Водород | 0 | 0,0090 |
| Меркурий | 20 | 0,0450 |
| Кислород | 20 | 0,0203 |
| Пар | 100 | 0,0130 |
| Жидкости | ||
| Вода | 0 | 1.792 |
| 20 | 1,002 | |
| 37 | 0,6947 | |
| 40 | 0,653 | |
| 100 | 0,282 | |
| Цельная кровь | 20 | 3,015 |
| 37 | 2,084 | |
| Плазма крови | 20 | 1,810 |
| 37 | 1,257 | |
| Спирт этиловый | 20 | 1. 20 20 |
| Метанол | 20 | 0,584 |
| Масло (тяжелая машина) | 20 | 660 |
| Масло (моторное, SAE 10) | 30 | 200 |
| Масло (оливковое) | 20 | 138 |
| Глицерин | 20 | 1500 |
| Мед | 20 | 2000–10000 |
| Кленовый сироп | 20 | 2000–3000 |
| Молоко | 20 | 3.0 |
| Масло (кукуруза) | 20 | 65 |
Ламинарный поток, ограниченный трубками — закон Пуазейля
Что вызывает поток? Ответ, что неудивительно, — разница в давлении. Фактически, существует очень простая взаимосвязь между горизонтальным потоком и давлением. Расход Q находится в направлении от высокого давления к низкому. Чем больше перепад давления между двумя точками, тем больше расход.%2024_img_0.jpg) Это отношение может быть указано как
Это отношение может быть указано как
[латекс] Q = \ frac {{P} _ {2} — {P} _ {1}} {R} \\ [/ latex],
, где P 1 и P 2 — это давления в двух точках, например, на обоих концах трубы, а R — сопротивление потоку. Сопротивление R включает все, кроме давления, которое влияет на скорость потока. Например, R больше для длинной трубки, чем для короткой.Чем больше вязкость жидкости, тем больше значение R . Турбулентность сильно увеличивается R , тогда как увеличение диаметра трубки уменьшает R . Если вязкость равна нулю, жидкость не имеет трения, и сопротивление потоку также равно нулю. Сравнивая поток без трения в трубе с вязким потоком, как показано на рисунке 4, мы видим, что для вязкой жидкости скорость максимальна в середине потока из-за сопротивления на границах. Мы можем видеть эффект вязкости в пламени горелки Бунзена, даже если вязкость природного газа мала. {4}} \\ [/ латекс].
{4}} \\ [/ латекс].
Это уравнение называется закон Пуазейля для сопротивления в честь французского ученого Ж. Л. Пуазейля (1799–1869), который вывел его в попытке понять поток крови, часто турбулентной жидкости.
Рис. 4. (a) Если поток жидкости в трубке имеет незначительное сопротивление, скорость по всей трубке одинакова. (b) Когда вязкая жидкость течет через трубку, ее скорость у стенок равна нулю, постоянно увеличиваясь до максимума в центре трубки.(c) Форма пламени горелки Бунзена обусловлена профилем скорости в трубе. (кредит: Джейсон Вудхед)
Давайте исследуем выражение Пуазейля для R , чтобы увидеть, имеет ли оно хороший интуитивный смысл. Мы видим, что сопротивление прямо пропорционально вязкости жидкости η и длине трубки л . В конце концов, оба эти фактора напрямую влияют на величину возникающего трения — чем оно больше, тем больше сопротивление и меньше поток.Радиус r трубки влияет на сопротивление, что опять же имеет смысл, потому что чем больше радиус, тем больше расход (все остальные факторы остаются неизменными). Но удивительно, что r возводится в четвертую степень в законе Пуазейля. Этот показатель означает, что любое изменение радиуса трубки очень сильно влияет на сопротивление. Например, удвоение радиуса трубки уменьшает сопротивление в 2 раза 4 = 16.{4}} {8 \ eta l} \\ [/ latex]
Но удивительно, что r возводится в четвертую степень в законе Пуазейля. Этот показатель означает, что любое изменение радиуса трубки очень сильно влияет на сопротивление. Например, удвоение радиуса трубки уменьшает сопротивление в 2 раза 4 = 16.{4}} {8 \ eta l} \\ [/ latex]
Это уравнение описывает ламинарный поток через трубку. Иногда его называют законом Пуазейля для ламинарного потока или просто законом Пуазейля .
Пример 1. Использование скорости потока: отложения зубного налета снижают кровотокПредположим, что скорость кровотока в коронарной артерии уменьшилась вдвое по сравнению с нормальным значением из-за отложений бляшек. За счет чего уменьшился радиус артерии, если не происходит турбулентности?
СтратегияПредполагая ламинарный поток, закон Пуазейля гласит, что
[латекс] Q = \ frac {\ left ({P} _ {2} — {P} _ {1} \ right) \ pi r ^ {4}} {8 \ eta l} \\ [/ latex] . {4} \\ [/ латекс].
{4} \\ [/ латекс].
Следовательно, r 2 = (0,5) 0,25 r 1 = 0,841 r 1 , уменьшение радиуса артерии на 16%.
ОбсуждениеЭто уменьшение радиуса на удивление мало для данной ситуации. Для восстановления кровотока, несмотря на это накопление, потребуется увеличение разницы давлений ( P 2 — P 1 ) в два раза с последующей нагрузкой на сердце.
Система кровообращения дает множество примеров действия закона Пуазейля — кровоток регулируется изменениями размера сосудов и кровяного давления. Кровеносные сосуды не жесткие, а эластичные. Регулировка кровотока в основном осуществляется путем изменения размера сосудов, поскольку сопротивление очень чувствительно к радиусу. Во время интенсивных упражнений кровеносные сосуды выборочно расширяются до важных мышц и органов, и повышается кровяное давление. Это увеличивает общий кровоток и увеличивает приток к определенным областям.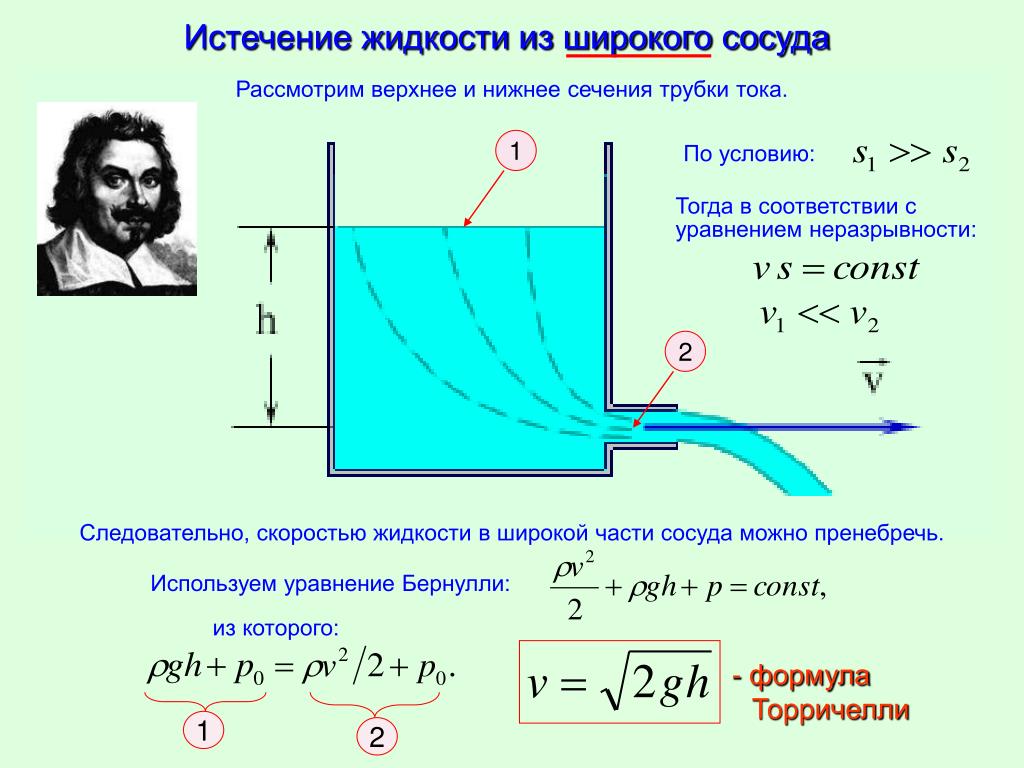 И наоборот, уменьшение радиуса сосудов, возможно, из-за бляшек в артериях, может значительно уменьшить кровоток. Если радиус судна уменьшается всего на 5% (до 0,95 от исходного значения), расход уменьшается примерно до (0,95) 4 = 0,81 от исходного значения. Уменьшение расхода на 19% вызвано уменьшением радиуса на 5%. Организм может компенсировать это повышением артериального давления на 19%, но это представляет опасность для сердца и любых сосудов с ослабленными стенками. Другой пример — автомобильное моторное масло.Если у вас есть автомобиль с манометром масла, вы можете заметить, что давление масла высокое, когда двигатель холодный. Вязкость моторного масла в холодном состоянии выше, чем в теплом, поэтому давление должно быть выше, чтобы перекачивать такое же количество холодного масла.
И наоборот, уменьшение радиуса сосудов, возможно, из-за бляшек в артериях, может значительно уменьшить кровоток. Если радиус судна уменьшается всего на 5% (до 0,95 от исходного значения), расход уменьшается примерно до (0,95) 4 = 0,81 от исходного значения. Уменьшение расхода на 19% вызвано уменьшением радиуса на 5%. Организм может компенсировать это повышением артериального давления на 19%, но это представляет опасность для сердца и любых сосудов с ослабленными стенками. Другой пример — автомобильное моторное масло.Если у вас есть автомобиль с манометром масла, вы можете заметить, что давление масла высокое, когда двигатель холодный. Вязкость моторного масла в холодном состоянии выше, чем в теплом, поэтому давление должно быть выше, чтобы перекачивать такое же количество холодного масла.
Рис. 5. Закон Пуазейля применяется к ламинарному течению несжимаемой жидкости с вязкостью η через трубку длиной l и радиусом r. Направление потока — от большего к меньшему давлению. Расход Q прямо пропорционален разности давлений P 2 — P 1 и обратно пропорционален длине л трубки и вязкости η жидкости.Расход увеличивается с r 4 , четвертой степени радиуса.
Расход Q прямо пропорционален разности давлений P 2 — P 1 и обратно пропорционален длине л трубки и вязкости η жидкости.Расход увеличивается с r 4 , четвертой степени радиуса.
Пример 2. Какое давление создает этот расход?
Внутривенная (IV) система подает физиологический раствор пациенту со скоростью 0,120 см. 3 / с через иглу радиусом 0,150 мм и длиной 2,50 см. Какое давление необходимо на входе иглы, чтобы вызвать этот поток, если считать, что вязкость физиологического раствора такая же, как у воды? Манометрическое давление крови в вене пациента — 8.{2} \ end {array} \\ [/ latex].
Обсуждение
Это давление может быть обеспечено с помощью баллона для внутривенного вливания с поверхностью физиологического раствора на 1,61 м над входом в иглу (это оставлено вам для решения в Задачах и упражнениях этой главы), при условии, что в системе имеется незначительное падение давления трубка, ведущая к игле.
Поток и сопротивление как причины падений давления
Возможно, вы заметили, что давление воды в вашем доме может быть ниже обычного в жаркие летние дни, когда больше используется.Это падение давления происходит в водопроводе еще до того, как оно достигнет вашего дома. Давайте рассмотрим поток через водопровод, как показано на рисунке 6. Мы можем понять, почему давление в доме P 1 падает во время интенсивного использования, переставив
[латекс] Q = \ frac {{P} _ {2} — {P} _ {1}} {R} \\ [/ latex]
Спо
[латекс] {P} _ {2} — {P} _ {1} = RQ \\ [/ latex],
, где в данном случае P 2 — давление на водопроводной станции, а R — сопротивление водопровода.Во время интенсивного использования расход Q велик. Это означает, что P 2 — P 1 также должны быть большими. Таким образом, P 1 должно уменьшиться. Правильно считать, что поток и сопротивление вызывают падение давления с P 2 до P 1 . P 2 — P 1 = RQ действительно как для ламинарных, так и для турбулентных потоков.
Правильно считать, что поток и сопротивление вызывают падение давления с P 2 до P 1 . P 2 — P 1 = RQ действительно как для ламинарных, так и для турбулентных потоков.
Рис. 6. Во время интенсивной эксплуатации наблюдается значительный перепад давления в водопроводе, и P 1 , поставляемое пользователям, значительно меньше, чем P 2 , созданное на водопроводных сооружениях. Если расход очень мал, то перепад давления незначителен, и P 2 ≈ P 1 .
Мы можем использовать P 2 — P 1 = RQ для анализа перепадов давления, возникающих в более сложных системах, в которых радиус трубы не везде одинаков.Сопротивление будет намного выше в узких местах, таких как закупорка коронарной артерии. Для заданного расхода Q перепад давления будет наибольшим там, где труба наиболее узкая. Так водопроводные краны управляют потоком. Кроме того, R сильно увеличивается из-за турбулентности, а сужение, которое создает турбулентность, значительно снижает давление ниже по потоку. Зубной налет в артерии снижает давление и, следовательно, поток, как за счет сопротивления, так и за счет создаваемой турбулентности.
Так водопроводные краны управляют потоком. Кроме того, R сильно увеличивается из-за турбулентности, а сужение, которое создает турбулентность, значительно снижает давление ниже по потоку. Зубной налет в артерии снижает давление и, следовательно, поток, как за счет сопротивления, так и за счет создаваемой турбулентности.
На рисунке 7 схематически изображена кровеносная система человека, показывающая среднее артериальное давление в ее основных частях для взрослого человека в состоянии покоя. Давление, создаваемое двумя насосами сердца, правым и левым желудочками, снижается за счет сопротивления кровеносных сосудов, когда кровь течет через них. Левый желудочек увеличивает артериальное давление, что приводит к току крови через все части тела, кроме легких. Правый желудочек получает кровь с низким давлением из двух основных вен и перекачивает ее через легкие для газообмена с атмосферными газами — удаления углекислого газа из крови и пополнения запасов кислорода. Схематически показан только один крупный орган с типичным разветвлением артерий на все более мелкие сосуды, самые маленькие из которых — капилляры, и воссоединение мелких вен с более крупными. Подобное разветвление происходит во множестве органов тела, и система кровообращения обладает значительной гибкостью в регулировании потока к этим органам за счет расширения и сужения артерий, ведущих к ним, и капилляров внутри них. Чувствительность потока к радиусу трубки делает эту гибкость возможной в большом диапазоне скоростей потока.
Схематически показан только один крупный орган с типичным разветвлением артерий на все более мелкие сосуды, самые маленькие из которых — капилляры, и воссоединение мелких вен с более крупными. Подобное разветвление происходит во множестве органов тела, и система кровообращения обладает значительной гибкостью в регулировании потока к этим органам за счет расширения и сужения артерий, ведущих к ним, и капилляров внутри них. Чувствительность потока к радиусу трубки делает эту гибкость возможной в большом диапазоне скоростей потока.
Рисунок 7. Схема кровеносной системы. Перепад давления создается двумя насосами в сердце и уменьшается за счет сопротивления сосудов. Разветвление сосудов в капилляры позволяет крови достигать отдельных клеток и обмениваться с ними веществами, такими как кислород и продукты жизнедеятельности. Система обладает впечатляющей способностью регулировать поток к отдельным органам, в основном за счет изменения диаметра сосудов.
Каждое разветвление более крупных сосудов на более мелкие увеличивает общую площадь поперечного сечения трубок, по которым течет кровь. Например, артерия с поперечным сечением 1 см 2 может разветвляться на 20 меньших артерий, каждая с поперечным сечением 0,5 см 2 , всего 10 см 2 . Таким образом снижается сопротивление разветвлений, так что давление полностью не теряется. Более того, поскольку [латекс] Q = A \ overline {v} \\ [/ latex] и A увеличивается за счет ветвления, средняя скорость кровотока в меньших сосудах снижается. Скорость крови в аорте (диаметр = 1 см) составляет около 25 см / с, в то время как в капиллярах (диаметром 20 мкм м) скорость составляет около 1 мм / с.Эта пониженная скорость позволяет крови обмениваться веществами с клетками капилляров и, в частности, альвеол.
Например, артерия с поперечным сечением 1 см 2 может разветвляться на 20 меньших артерий, каждая с поперечным сечением 0,5 см 2 , всего 10 см 2 . Таким образом снижается сопротивление разветвлений, так что давление полностью не теряется. Более того, поскольку [латекс] Q = A \ overline {v} \\ [/ latex] и A увеличивается за счет ветвления, средняя скорость кровотока в меньших сосудах снижается. Скорость крови в аорте (диаметр = 1 см) составляет около 25 см / с, в то время как в капиллярах (диаметром 20 мкм м) скорость составляет около 1 мм / с.Эта пониженная скорость позволяет крови обмениваться веществами с клетками капилляров и, в частности, альвеол.
Сводка раздела
- Ламинарный поток характеризуется плавным течением жидкости слоями, которые не смешиваются.
- Турбулентность характеризуется вихрями и завихрениями, которые смешивают слои жидкости вместе.
- Вязкость жидкости [латекс] \ эта [/ латекс] обусловлена трением внутри жидкости.
 Типичные значения приведены в таблице 1.{4}} {8 \ eta l} \\ [/ латекс].
Типичные значения приведены в таблице 1.{4}} {8 \ eta l} \\ [/ латекс]. - Падение давления, вызванное потоком и сопротивлением, определяется по формуле
[латекс] {P} _ {2} — {P} _ {1} = RQ [/ латекс].
Концептуальные вопросы
1. Объясните, почему вязкость жидкости уменьшается с температурой, то есть как повышение температуры может уменьшить влияние сил сцепления в жидкости? Также объясните, почему вязкость газа увеличивается с температурой, то есть как повышение температуры газа приводит к большему количеству столкновений между атомами и молекулами?
2.При гребле на каноэ вверх по течению разумнее всего плыть как можно ближе к берегу. Во время плавания на каноэ вниз по течению лучше держаться посередине. Объяснить, почему.
3. Почему в душе уменьшается поток, когда кто-то смывает воду из унитаза?
4. Сантехника обычно включает заполненные воздухом трубы возле водопроводных кранов, как показано на рисунке 8. Объясните, зачем они нужны и как они работают.
Объясните, зачем они нужны и как они работают.
Рис. 8. Вертикальная трубка рядом с водопроводным краном остается наполненной воздухом и служит полезной цели.
Задачи и упражнения
1. (a) Рассчитайте замедляющую силу, обусловленную вязкостью слоя воздуха между тележкой и ровной воздушной дорожкой, учитывая следующую информацию: температура воздуха 20º C, тележка движется со скоростью 0,400 м / с, площадь ее поверхности составляет 2,50 × 10 -2 м 2 , а толщина воздушной прослойки составляет 6,00 × 10 -5 м. б) Каково отношение этой силы к весу тележки весом 0,300 кг?
2. Какое усилие необходимо, чтобы натянуть одно предметное стекло микроскопа на другое со скоростью 1?00 см / с, если между ними находится слой воды толщиной 20,0º толщиной 0,500 мм и площадь контакта 8,00 см 2 ?
3. Раствор глюкозы, вводимый внутривенно, имеет скорость потока 4,00 см. 3 / мин. Какой будет новый расход, если глюкозу заменить цельной кровью, имеющей такую же плотность, но вязкость в 2,50 раза больше, чем у глюкозы? Все остальные факторы остаются неизменными.
4. Перепад давления по длине артерии 100 Па, радиус 10 мм, поток ламинарный.Средняя скорость кровотока 15 мм / с. а) Какова суммарная сила, действующая на кровь в этом участке артерии? б) Какая сила расходуется на поддержание потока?
5. Маленькая артерия имеет длину 1,1 × 10 -3 и радиус 2,5 × 10 -5 . Если перепад давления в артерии составляет 1,3 кПа, какова скорость потока через артерию? (Предположим, что температура 37ºC.)
6. Изначально жидкость течет по трубке со скоростью 100 см. 3 / с.Чтобы проиллюстрировать чувствительность расхода к различным факторам, рассчитайте новый расход для следующих изменений, оставив все остальные факторы такими же, как в исходных условиях. (а) Перепад давления увеличивается в 1,50 раза. (b) Заменяется новая жидкость с вязкостью в 3,00 раза большей. (c) Трубку заменяют на трубку, длина которой в 4 раза больше. (d) Используется другая трубка с радиусом в 0,100 раза больше исходного. (e) заменяется еще одна трубка с радиусом в 0,100 раза больше исходного и половиной длины, и , перепад давления увеличивается в 1 раз.50.
(e) заменяется еще одна трубка с радиусом в 0,100 раза больше исходного и половиной длины, и , перепад давления увеличивается в 1 раз.50.
7. Артериолы (маленькие артерии), ведущие к органу, сужаются, чтобы уменьшить приток к органу. Чтобы выключить орган, кровоток естественным образом снижается до 1,00% от исходного значения. Насколько уменьшились радиусы артериол? Пингвины делают это, когда стоят на льду, чтобы уменьшить кровоток к ногам.
8. Ангиопластика — это метод, при котором артерии, частично заблокированные бляшками, расширяются для увеличения кровотока. В какой степени необходимо увеличить радиус артерии, чтобы увеличить кровоток в 10 раз?
9.(а) Предположим, что радиус кровеносного сосуда уменьшился до 90,0% от его первоначального значения из-за отложений зубного налета, и организм компенсирует это за счет увеличения разницы давлений вдоль сосуда, чтобы поддерживать постоянную скорость потока. Во сколько раз должен увеличиваться перепад давления? (b) Если препятствие создает турбулентность, какое дополнительное влияние это может оказать на скорость потока?
10. Сферическая частица, падающая с конечной скоростью в жидкости, должна иметь гравитационную силу, уравновешенную силой сопротивления и выталкивающей силой.{2} g} {9 \ eta} \ left ({\ rho} _ {\ text {s}} — {\ rho} _ {1} \ right) \\ [/ latex],
Сферическая частица, падающая с конечной скоростью в жидкости, должна иметь гравитационную силу, уравновешенную силой сопротивления и выталкивающей силой.{2} g} {9 \ eta} \ left ({\ rho} _ {\ text {s}} — {\ rho} _ {1} \ right) \\ [/ latex],
, где R — радиус сферы, ρ s — ее плотность, ρ 1 — плотность жидкости и η коэффициент вязкости.
11. Используя уравнение предыдущей задачи, найдите вязкость моторного масла, в которое стальной шарик радиусом 0,8 мм падает с конечной скоростью 4,32 см / с. Плотность шара и масла 7.{\ text {2}} \\ [/ latex] и установив это значение, равное весу человека, найдите предельную скорость для человека, падающего с «распростертым орлом». Найдите формулу и число для v t с предположениями относительно размера.
13. Между двумя предметными стеклами микроскопа помещен слой масла толщиной 1,50 мм. Исследователи обнаружили, что сила 5,50 × 10 -4 Н требуется для скольжения друг над другом со скоростью 1,00 см / с, когда их контактная площадь составляет 6,00 см. 2 . Какая вязкость масла? Что это за масло?
2 . Какая вязкость масла? Что это за масло?
14.(a) Убедитесь, что уменьшение ламинарного потока через трубу на 19,0% вызвано уменьшением радиуса на 5,00%, при условии, что все другие факторы остаются постоянными, как указано в тексте. (b) Какое увеличение потока получается при увеличении радиуса на 5,00%, опять же при условии, что все другие факторы остаются постоянными?
15. Пример 1 выше относится к потоку физиологического раствора в системе IV. (a) Убедитесь, что давление 1,62 × 10 4 Н / м 2 создается на глубине 1,61 м в солевом растворе, предполагая, что его плотность соответствует плотности морской воды.(b) Рассчитайте новый расход, если высота солевого раствора уменьшится до 1,50 м. (c) На какой высоте направление потока изменится на противоположное? (Этот поворот может быть проблемой, когда пациенты встают.)
16. Когда врачи диагностируют артериальную закупорку, они указывают снижение скорости потока.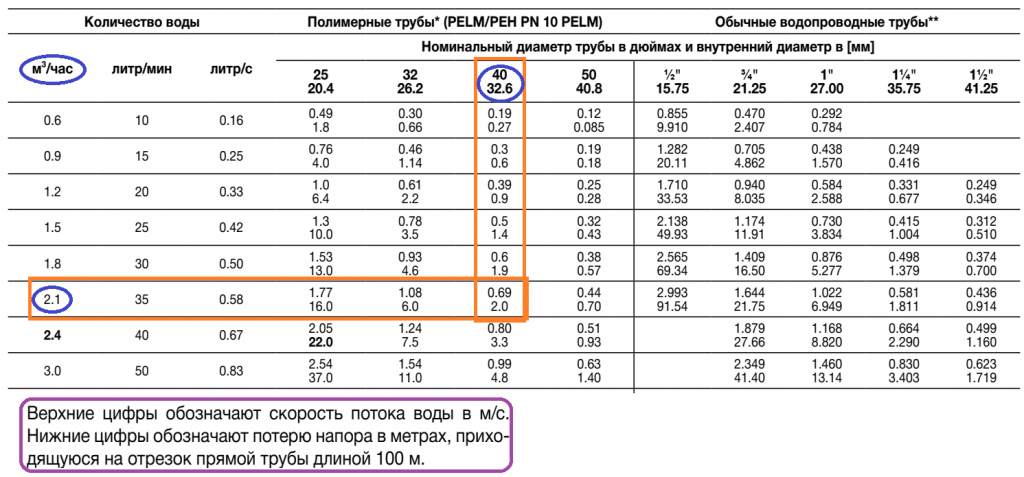 Если скорость потока в артерии была снижена до 10,0% от своего нормального значения из-за сгустка крови, а средняя разница давления увеличилась на 20,0%, в какой степени сгусток уменьшил радиус артерии?
Если скорость потока в артерии была снижена до 10,0% от своего нормального значения из-за сгустка крови, а средняя разница давления увеличилась на 20,0%, в какой степени сгусток уменьшил радиус артерии?
17.Во время марафонского забега кровоток бегуна увеличивается в 10 раз от ее частоты отдыха. Вязкость ее крови упала до 95,0% от нормального значения, а разница артериального давления в кровеносной системе увеличилась на 50,0%. Во сколько раз увеличился средний радиус ее кровеносных сосудов?
18. Вода, подаваемая в дом по водопроводу, имеет давление 3,00 × 10 5 в начале летнего дня, когда потребление по соседству мало. Это давление создает поток 20.0 л / мин через садовый шланг. Позже днем давление на выходе из водопровода и входе в дом падает, и через тот же шланг получается поток всего 8,00 л / мин. а) Какое давление сейчас подается в дом, если сопротивление постоянное? (b) На какой фактор увеличился расход в водопроводной магистрали, чтобы вызвать это снижение подаваемого давления? Давление на входе в водовод составляет 5,00 × 10 5 Н / м, а исходный расход составлял 200 л / мин. (c) Сколько еще пользователей, если предположить, что каждый будет потреблять 20,0 л / мин утром?
(c) Сколько еще пользователей, если предположить, что каждый будет потреблять 20,0 л / мин утром?
19. Нефтяной фонтан выбрасывает сырую нефть на 25,0 м в воздух по трубе диаметром 0,100 м. Пренебрегая сопротивлением воздуха, но не сопротивлением трубы, и предполагая ламинарный поток, рассчитайте манометрическое давление на входе в вертикальную трубу длиной 50,0 м. Примем плотность масла 900 кг / м 3 и вязкость 1,00 (Н / м 2 ) с (или 1,00 Па с).Учтите, что необходимо учитывать давление из-за 50-метрового столба масла в трубе.
20. Бетон перекачивается из бетономешалки к месту укладки, а не в тачках. Скорость потока составляет 200,0 л / мин через шланг длиной 50,0 м и диаметром 8,00 см, а давление в насосе составляет 8,00 × 10 6 Н / м 2 . (а) Рассчитайте сопротивление шланга. б) Какова вязкость бетона, если предположить, что поток ламинарный? (c) Какая мощность подается, если предположить, что точка использования находится на том же уровне, что и насос? Вы можете пренебречь мощностью, подаваемой для увеличения скорости бетона.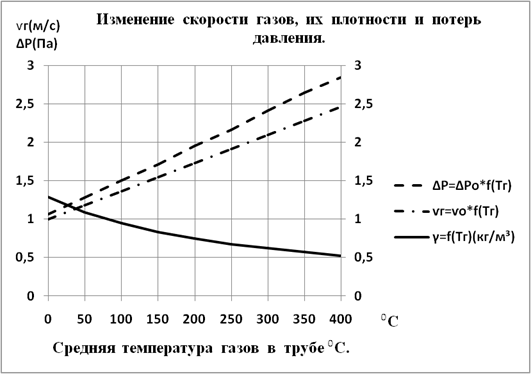
21. Создай свою проблему Рассмотрим коронарную артерию, суженную из-за артериосклероза. Постройте задачу, в которой вы вычисляете величину уменьшения диаметра артерии на основе оценки уменьшения скорости потока.
22. Представьте себе реку, которая протекает в районе дельты на пути к морю. Постройте задачу, в которой вы вычисляете среднюю скорость, с которой вода движется в районе дельты, на основе скорости, с которой она движется вверх по реке.Среди вещей, которые следует учитывать, — размер и скорость потока реки до того, как она расширится, и ее размер после того, как она расширится. Вы можете построить задачу для реки, которая переходит в одну большую реку или на несколько меньших рек.
Глоссарий
- ламинарный:
- тип потока жидкости, в котором слои не смешиваются
- турбулентность:
- поток жидкости, в котором слои смешиваются вместе посредством завихрений и завихрений
- вязкость:
- трение в жидкости, определяемое как трение между слоями
- Закон Пуазейля для сопротивления:
- сопротивление ламинарному течению несжимаемой жидкости в трубке: R = 8 ηl / πr 4
- Закон Пуазейля:
- скорость ламинарного течения несжимаемой жидкости в трубке: Q = ( P 2 — P 1 ) πr 4 /8 ηl
Избранные решения проблем и упражнения
1. (а) 3.02 × 10 -3 Н (б) 1.03 × 10 -3
(а) 3.02 × 10 -3 Н (б) 1.03 × 10 -3
3. 1.60 см 3 / мин
5. 8,7 × 1o -11 м 3 / с
7. 0,316
9. (a) 1,52 (b) Турбулентность снизит скорость кровотока, что потребует еще большего увеличения разницы давлений, что приведет к повышению артериального давления.
11,225 мПа с
13. 0,138 Па с или оливковое масло.
15. (а) 1.62 × 10 4 Н / м 2 (б) 0.111 см 3 / с (в) 10,6 см
17. 1,59
19. 2,95 × 10 6 Н / м 2 (избыточное давление)
Как жидкость течет в трубах — Accendo Reliability
Жидкость — это жидкость или газ. В промышленности они перекачиваются от хранилища к месту использования. Правильная конструкция и установка системы трубопроводов сводят к минимуму потери давления и улучшают характеристики оборудования и процессов.
В этой статье кратко объясняется, что происходит с жидкостями, протекающими по трубам.
Стенка трубы
Жидкость, протекающая по трубе, контактирует со стенкой трубы. Стенка трубы имеет шероховатость поверхности. Степень шероховатости влияет на сопротивление жидкости. Шероховатость измеряется высотой выступов, выступающих из стенки трубы.
В ложбинах между выступами жидкость движется медленно. Выше проекций он движется быстрее. Сопротивление между слоями разрывает или разрывает их, и каждый слой движется с разной скоростью. Скорость сдвига уменьшается по мере удаления от стены.Скорость у стены равна нулю и самая высокая в центре. Это означает, что центральная сердцевина жидкости выходит из трубы первой.
Рисунок 1. Скорости потока через трение трубыи ламинарный подслой
Из-за трения, вызываемого стенкой трубы, жидкость движется к стенке медленнее. Эта медленно движущаяся жидкость известна как ламинарный подслой. В этом слое жидкость скользит по себе. Толщина подслоя может варьироваться от десятых долей миллиметра до нескольких миллиметров в зависимости от скорости потока, высоты выступов стенок и физических свойств жидкости. Подслой развивается только в турбулентных (быстрых) потоках. При медленных потоках подслой сливается с пластинчатым (медленным) потоком в трубе. На рисунке 1 показано влияние на скорость потока поверхности стенки трубы.
Подслой развивается только в турбулентных (быстрых) потоках. При медленных потоках подслой сливается с пластинчатым (медленным) потоком в трубе. На рисунке 1 показано влияние на скорость потока поверхности стенки трубы.
Вдали от стенки трубы поток турбулентный. В этой области есть водовороты и вихри, беспорядочно перемещающиеся по трубе из стороны в сторону и сверху вниз. Это область, где беспорядочные комки жидкости «болтают» по трубе. Между ламинарной и турбулентной областями находится короткая переходная зона, поскольку поток меняется на турбулентный.
Влияние вязкости и плотности
Не все жидкости ведут себя одинаково. Кровь имеет другие характеристики потока, чем вода. Краска течет иначе, чем бензин. Жидкости классифицируются по их поведению при сдвиге. Те жидкости, которые имеют постоянную скорость сдвига с изменением скорости (например, вода), называются ньютоновскими (Ньютон первым разработал математическое объяснение этого явления). Те, у которых скорость сдвига меняется с изменением скорости (например, краска и кровь), являются неньютоновскими.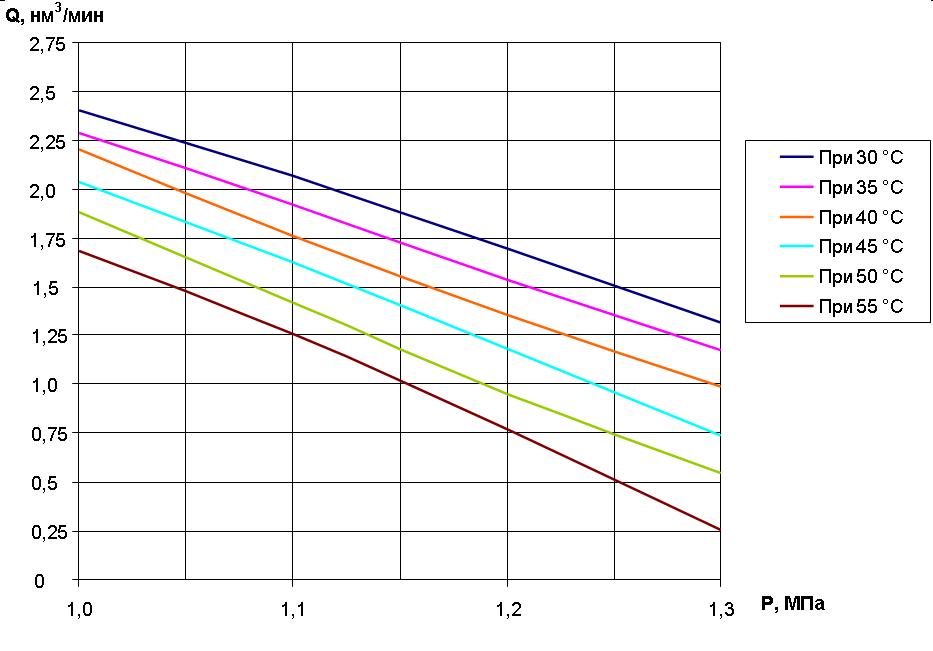 Скорость сдвига является мерой вязкости или скользкости жидкости.
Скорость сдвига является мерой вязкости или скользкости жидкости.
Плотность жидкости влияет на ее вязкость. Жидкости с большей массой на единицу объема тяжелее и требуют больше энергии для их перемещения и менее легкого сдвига. Повышение температуры снижает вязкость и плотность жидкостей.
Чем более вязкая или менее скользкая жидкость, тем труднее добиться сдвига между слоями. Высокая вязкость предотвращает резкие изменения скорости между слоями. Подслой в вязких жидкостях толще, чем в жидкостях с низкой вязкостью.
Эффекты скорости
На низких скоростях весь поток через трубу ламинарный, и жидкость скользит по самой себе. По мере того, как скорость увеличивается, начинают формироваться водовороты, которые пересекают слои жидкости. Развивается переход от ламинарного течения к турбулентному. При еще более высоких скоростях поток в сердцевине трубы становится турбулентным с закрученными вихрями повсюду. На рисунке 2 показано, где возникают различные области потока на сопле резервуара.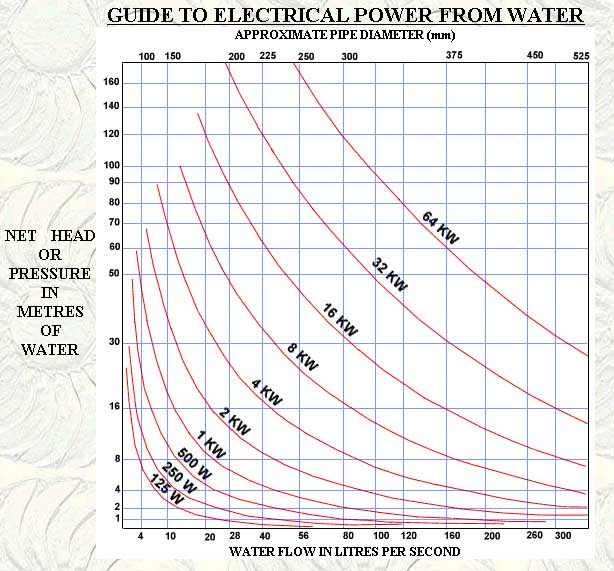
Ламинарный подслой всегда присутствует у стенки трубы.Но по мере того, как скорость увеличивается, энергетические закрученные водовороты начинают воздействовать более глубоко, и подслой начинает истончаться. При еще более высоких скоростях подслой утончается еще больше, и более высокие пики шероховатости остаются в турбулентной области. Если подслой покрывает выступы шероховатостей, стена считается «гладкой». Когда шероховатость стены выходит из подслоя, стена считается «шероховатой». Это означает, что одна и та же стенка может быть как гладкой, так и шероховатой, в зависимости от скорости жидкости.
Эксперименты доказали, что потеря давления в трубе с ламинарным потоком пропорциональна скорости (p ∝ V), тогда как для турбулентного потока потеря давления пропорциональна квадрату скорости (p ∝ V2).Более медленный поток позволяет получить более толстый подслой и создает «гладкую» стенку трубы. Это сводит к минимуму потери по трубе. В турбулентном потоке потеря давления намного больше.
В турбулентном потоке потеря давления намного больше.
Проектировщик трубопроводной системы должен найти практический баланс между увеличением диаметра трубы для снижения потерь энергии и сохранением небольшого диаметра для снижения затрат на установку.
Незначительные потери в фитингах Piper
Колена, отводы, переходники, тройники и фланцы — все это приводит к незначительным индивидуальным потерям давления.Когда жидкость вынуждена менять направление или обходить разрушение, образуются водовороты. Эти новые закручивающиеся вихри нарушают структуру потока и создают дополнительные потери давления.
Наибольшие потери давления происходят при резких изменениях диаметра и направления. Большая часть потерь приходится на вихревой след ниже по потоку. При проектировании участка трубопровода постепенное изменение схемы потока.
Расход газа
В отличие от жидкости газ сжимаем и его можно сжать.Когда газ сжимается, его плотность увеличивается — по мере сброса давления плотность уменьшается. Газ, поступающий в трубу, начинается при определенном давлении, температуре и соответствующей плотности. Потери на трение по трубе вызывают потерю давления. Если теперь газ находится под более низким давлением, он должен иметь соответственно меньшую плотность. (Он меньше сдавлен, чем был в начале.) Это означает, что плотность текущего газа изменяется по длине трубы. Эффект сильнее при высоких скоростях.
Газ, поступающий в трубу, начинается при определенном давлении, температуре и соответствующей плотности. Потери на трение по трубе вызывают потерю давления. Если теперь газ находится под более низким давлением, он должен иметь соответственно меньшую плотность. (Он меньше сдавлен, чем был в начале.) Это означает, что плотность текущего газа изменяется по длине трубы. Эффект сильнее при высоких скоростях.
Для того, чтобы масса газа попала в трубу, такая же масса должна покинуть трубу. Мы знаем, что плотность постоянно уменьшается по мере падения давления в трубе. Один килограмм менее плотного газа требует больше места (объема), чем такой же вес более сжатого газа. Чтобы получить один килограмм расширяющегося газа, который занимает больше объема, из конца трубы он должен идти быстрее, чем когда он входил в трубу. Газ, протекающий по трубе, расширяется при падении давления и ускоряется по мере продвижения по трубе.
Расширяющийся газ охлаждается. Этот принцип используется в холодильниках и кондиционерах.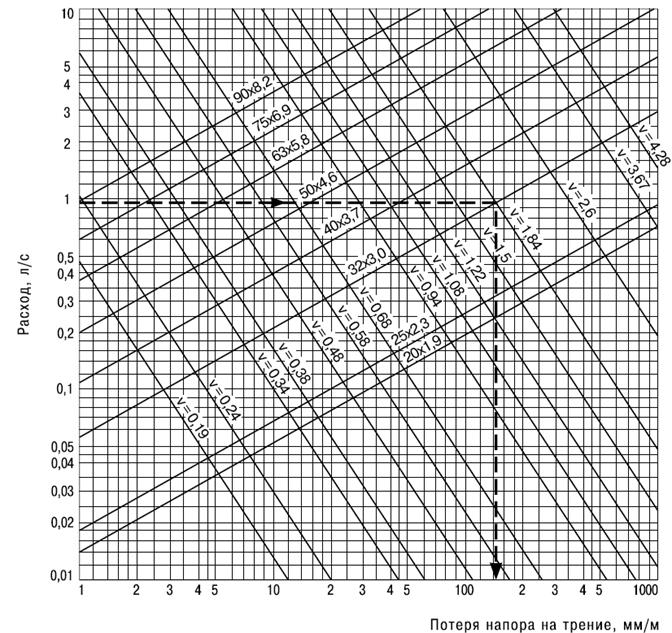 Газ, текущий в трубе, расширяется при падении плотности. Вот почему трубопроводы сжатого воздуха холодные на ощупь, а капли воды собираются в приводах пневматических клапанов. Температура упала достаточно низко, чтобы конденсировать водяной пар.
Газ, текущий в трубе, расширяется при падении плотности. Вот почему трубопроводы сжатого воздуха холодные на ощупь, а капли воды собираются в приводах пневматических клапанов. Температура упала достаточно низко, чтобы конденсировать водяной пар.
Майк Сондалини — инженер по техническому обслуживанию
Мы (Accendo Reliability) опубликовали эту статью с любезного разрешения Feed Forward Publishing, дочерней компании BIN95.com
Интернет: trade-school.education
Эл. Почта: [email protected]
Если вам это показалось интересным, вам может понравиться электронная книга Process Control Essentials.
Калькулятор расхода трубы| Уравнение Хазена-Вильямса
Уравнение Хазена-Вильямса
Уравнение Хазена-Вильямса — это эмпирически выведенная формула, описывающая скорость воды в гравитационном потоке. Помните, что уравнение Хейзена-Вильямса справедливо только для воды — его применение для любой другой жидкости даст вам неточные результаты. Он также не учитывает температуру воды и является точным только для диапазона 40–75 ° F (4–25 ° C).
Он также не учитывает температуру воды и является точным только для диапазона 40–75 ° F (4–25 ° C).
Вы можете записать эту формулу как:
v = k * C * R 0,63 * S 0,54
где:
- v обозначает скорость воды, текущей в трубе (в м / с для метрической системы и фут / с для британской системы мер)
- C — коэффициент шероховатости
- R означает гидравлический радиус (в метрах или футах в зависимости от системы единиц)
- S — наклон энергетической линии (потеря напора на трение на длину трубы).Он безразмерный, но иногда выражается в м / м.
- k — коэффициент преобразования, зависящий от системы единиц (k = 0,849 для метрической системы и k = 1,318 для британской системы)
Вам не нужно знать значения C , R или S , чтобы использовать наш калькулятор расхода трубы — мы рассчитаем их для вас!
Коэффициент шероховатости C зависит от материала трубы. Вы можете выбрать материал из раскрывающегося списка или ввести значение C вручную, если вам известен коэффициент шероховатости вашей проточной системы.Мы используем следующие значения:
Вы можете выбрать материал из раскрывающегося списка или ввести значение C вручную, если вам известен коэффициент шероховатости вашей проточной системы.Мы используем следующие значения:
| Материал | Коэффициент шероховатости |
|---|---|
| Чугун | 100 |
| Бетон | 110 |
| Медь | 140 |
| Пластик | 150 |
| Сталь | 120 |
Гидравлический радиус , R, — это пропорция между площадью и периметром трубы.Если труба круглая, вы найдете ее по следующему уравнению:
R = A / P = πr² / 2πr = r / 2 = d / 4
, где r — радиус трубы, а d — диаметр трубы.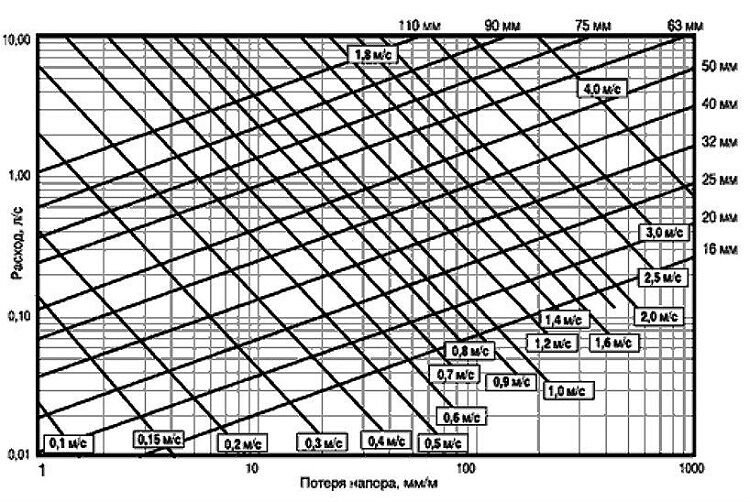 Вы можете просмотреть и изменить все эти параметры (площадь, периметр, гидравлический радиус) в расширенном режиме этого калькулятора расхода трубы.
Вы можете просмотреть и изменить все эти параметры (площадь, периметр, гидравлический радиус) в расширенном режиме этого калькулятора расхода трубы.
Чтобы рассчитать уклон , S, , необходимо разделить длину трубы на перепад (разница высот между начальной и конечной точками).Помните, что если наклон трубы непостоянен, а постоянно меняется, реальная скорость потока воды будет отличаться от полученного результата.
Если вы знаете скорость гравитационного потока, вы также можете найти расход , Q, , умножив площадь поперечного сечения трубы на скорость потока:
Q = A * v
Обязательно используйте наш калькулятор расхода для преобразования расхода (объемного расхода) и массового расхода.
Основы теории вакуума
Как и в любой другой дисциплине, понимание основных научных принципов имеет глубокие практические последствия при правильном понимании. В этой серии статей мы рассмотрим первые принципы вакуумной технологии и объясним их с помощью реальных иллюстраций. Большинство промышленных вакуумных систем в широком смысле можно разделить на следующие категории: низкий (то есть «мягкий»), средний, высокий (то есть «жесткий») и сверхвысокий вакуум (таблица 1).Эти диапазоны очень полезны при описании различного давления, расхода и других возникающих явлений, что приводит к лучшему пониманию выбора и работы вакуумного насоса, а также эксплуатационных требований системы при различных уровнях вакуума.
Большинство промышленных вакуумных систем в широком смысле можно разделить на следующие категории: низкий (то есть «мягкий»), средний, высокий (то есть «жесткий») и сверхвысокий вакуум (таблица 1).Эти диапазоны очень полезны при описании различного давления, расхода и других возникающих явлений, что приводит к лучшему пониманию выбора и работы вакуумного насоса, а также эксплуатационных требований системы при различных уровнях вакуума.
Как показывает разница в давлении от низкого до сверхвысокого вакуума, промышленные вакуумные системы должны работать в чрезвычайно широком диапазоне давлений.На самом деле диапазон настолько велик, что его трудно понять. Рассмотрим объем газа под давлением 1000 мбар (атмосферное давление) в контейнере размером 1 метр на 1 метр на 1 метр, запечатанном так, чтобы никакие молекулы не могли выйти или проникнуть внутрь.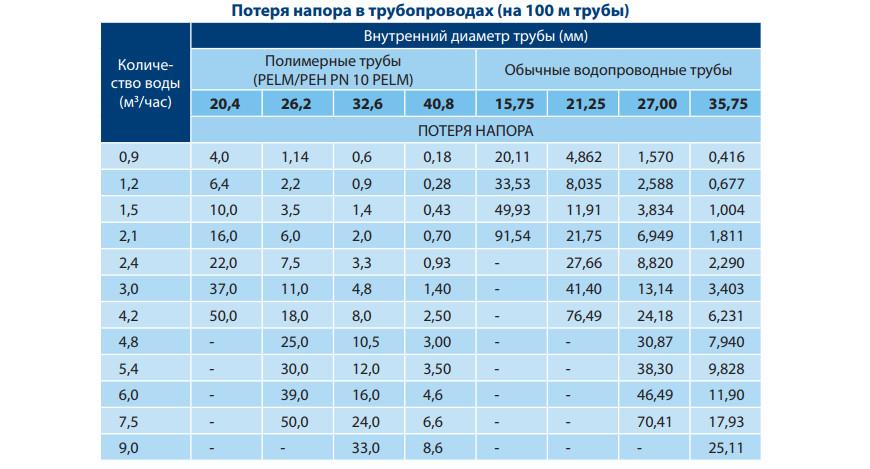 Легко понять, что если контейнер расширяется в объеме, оставаясь закрытым, давление будет уменьшаться (и создается вакуум) прямо пропорционально увеличению объема (в соответствии с законом Бойля). Если, например, объем емкости увеличится вдвое до 2 кубометров, давление упадет вдвое, до 500 мбар.Когда это отношение распространяется до масштаба промышленных вакуумных систем, результат впечатляет. Если мы возьмем тот же объем газа в 1 кубический метр и увеличим его объем настолько, чтобы давление снизилось до 10 -12 мбар (сверхвысокий вакуум), контейнер будет ошеломляющим в длину 99 км x ширину 99 км x Высота 99 км, что в 200 раз превышает объем грандиозного каньона!
Легко понять, что если контейнер расширяется в объеме, оставаясь закрытым, давление будет уменьшаться (и создается вакуум) прямо пропорционально увеличению объема (в соответствии с законом Бойля). Если, например, объем емкости увеличится вдвое до 2 кубометров, давление упадет вдвое, до 500 мбар.Когда это отношение распространяется до масштаба промышленных вакуумных систем, результат впечатляет. Если мы возьмем тот же объем газа в 1 кубический метр и увеличим его объем настолько, чтобы давление снизилось до 10 -12 мбар (сверхвысокий вакуум), контейнер будет ошеломляющим в длину 99 км x ширину 99 км x Высота 99 км, что в 200 раз превышает объем грандиозного каньона!
Другой способ понять диапазон рабочего давления промышленных вакуумных систем — это рассмотреть плотность газа или количество молекул газа, находящихся в заданном объеме.Приблизительно 2,65 x 10 19 или 26 500 000 000 000 000 000 молекул в кубическом сантиметре газа при 10 3 мбар, что соответствует атмосферному давлению на уровне моря (Таблица 2). При все меньшем и меньшем давлении молекулы распространяются все дальше и дальше, пока в сверхвысоком вакууме (10 — 12 мбар) не будет только 2,65 x 104 или 26 500 молекул на кубический сантиметр. При такой плотности примерно на каждые 0,33 мм в пространстве имеется только одна молекула. Поскольку диаметр каждой молекулы газа намного меньше этого (например, 4 x 10 -8 см для воздуха), между молекулами остается большое пространство.Чтобы выразить это пропорционально, если бы молекулы газа были песчинками, в сверхвысоком вакууме они были бы на расстоянии 1650 метров друг от друга. При таких чрезвычайно низких давлениях столкновения между молекулами, которые обычно определяют свойства газов, становятся очень редкими, и для объяснения их свойств требуется другая теоретическая модель (так называемая кинетическая теория газов).
При все меньшем и меньшем давлении молекулы распространяются все дальше и дальше, пока в сверхвысоком вакууме (10 — 12 мбар) не будет только 2,65 x 104 или 26 500 молекул на кубический сантиметр. При такой плотности примерно на каждые 0,33 мм в пространстве имеется только одна молекула. Поскольку диаметр каждой молекулы газа намного меньше этого (например, 4 x 10 -8 см для воздуха), между молекулами остается большое пространство.Чтобы выразить это пропорционально, если бы молекулы газа были песчинками, в сверхвысоком вакууме они были бы на расстоянии 1650 метров друг от друга. При таких чрезвычайно низких давлениях столкновения между молекулами, которые обычно определяют свойства газов, становятся очень редкими, и для объяснения их свойств требуется другая теоретическая модель (так называемая кинетическая теория газов).
Теория сплошной среды и кинетическая теория газов
При атмосферном или близком к нему давлении и в невакуумных системах так называемая теория континуума точно описывает свойства газов. Проще говоря, это говорит нам о том, что столкновения между молекулами газа определяют свойства газа. Теория континуума — это то, что мы называем макроскопической по своей природе, и регулируется газовыми законами, такими как закон идеального газа, закон Бойлса и закон Дальтона.
Проще говоря, это говорит нам о том, что столкновения между молекулами газа определяют свойства газа. Теория континуума — это то, что мы называем макроскопической по своей природе, и регулируется газовыми законами, такими как закон идеального газа, закон Бойлса и закон Дальтона.
- Закон идеального газа: В идеальном или идеальном газе изменение плотности напрямую связано с изменением как температуры, так и давления
- Закон Бойлса: давление, оказываемое данной массой идеального газа, обратно пропорционально занимаемому им объему при постоянной температуре
- Закон парциальных давлений Дальтона: в смеси нереагирующих газов полное оказываемое давление равно сумме парциальных давлений отдельных газов
После того, как технология вакуумных насосов достигла такой степени, что все меньше и меньше молекул газа стало возможным в данном объеме, основные принципы, влияющие на свойства этих газов, изменились, и молекулярные соображения стали первостепенными. А именно, молекулы газа становятся настолько разбросанными, что межмолекулярные столкновения между молекулами газа больше не доминируют, а, скорее, столкновения со стенками камеры были определяющим фактором, влияющим на свойства газа. Это привело к созданию кинетической теории газов, которая применима не только при низких давлениях (высоком вакууме), но и точна во всем диапазоне давлений, наблюдаемых в промышленных вакуумных системах.
А именно, молекулы газа становятся настолько разбросанными, что межмолекулярные столкновения между молекулами газа больше не доминируют, а, скорее, столкновения со стенками камеры были определяющим фактором, влияющим на свойства газа. Это привело к созданию кинетической теории газов, которая применима не только при низких давлениях (высоком вакууме), но и точна во всем диапазоне давлений, наблюдаемых в промышленных вакуумных системах.
Молекулярная плотность и длина свободного пробега
Основная концепция кинетической теории состоит в том, что газ состоит из большого числа отдельных частиц (молекул), каждая из которых движется индивидуально и беспорядочно, и что столкновения между ними, а также их столкновения со стенками сосуда, определяют давление, создаваемое газ.Молекулярная плотность или количество молекул газа в единице объема (таблица 2) изменяется пропорционально давлению. Кроме того, длина свободного пробега (или среднее расстояние, которое должна пройти молекула, прежде чем столкнуться с другой молекулой) значительно увеличивается с уменьшением давления (рис. 2). Наиболее важно то, что увеличенная длина свободного пробега при пониженном давлении диктует, что столкновения молекул со стенками сосуда определяют свойства газа при пониженном давлении.
2). Наиболее важно то, что увеличенная длина свободного пробега при пониженном давлении диктует, что столкновения молекул со стенками сосуда определяют свойства газа при пониженном давлении.
Обратите внимание на этом рисунке, что при сверхвысоком вакууме 10 -10 мбар среднее значение свободного путь составляет почти 10 5 или 100 000 метров.Это означает, что столкновения между молекулами газа настолько редки, что каждая молекула должна пройти в среднем 100000 метров до случайного столкновения с другой молекулой. Поскольку стороны сосуда расположены намного ближе, столкновения со стенкой сосуда происходят гораздо чаще, чем с другими молекулами. По этой причине при высоком и сверхвысоком вакууме столкновения молекул со стенками сосуда (рис. 3) определяют давление, оказываемое газом на стенки сосуда.
Это понимание приводит к формулировке давления газа как функции плотности газа, (средней квадратичной) скорости и длины свободного пробега отдельного газа. молекулы.На этой основе, называемой кинетической теорией газов, производятся расчеты давления, расхода и проводимости во всем рабочем диапазоне вакуума.
Теория кинетического газа основана на следующих пяти предположениях.
- Газы состоят из большого количества частиц, которые ведут себя как неупругие сферические объекты в состоянии постоянного случайного движения.
- Частицы движутся линейно, пока не столкнутся с другой частицей или стенками своего контейнера.
- Размер частиц незначителен по сравнению с пространством между ними, поэтому большая часть объема газа состоит из пустого пространства.
- Нет силы притяжения или отталкивания между частицами газа или между частицами и стенками их контейнера, и поэтому их полная энергия просто равна их кинетической энергии.

- Столкновения между частицами газа и столкновения со стенками контейнера 100% упругие. Энергия частицы газа не теряется при столкновении с другой частицей или стенками контейнера.
Принимая во внимание сделанные выше предположения, мы можем вывести формулу (Уравнение 1) для описания давления газа в соответствии с кинетической теорией газа.
Вышеизложенное относится к принципу классической механики, где кинетическая энергия = 1/2 мВ 2 , разработанному Лейбницем и Бернулли и первоначально описанному в 1722 году Грейвзандом в серии экспериментов, в которых латунные шары сбрасывались с разной высоты на мягкая глиняная поверхность. Грейвсанд обнаружил, что шар, скорость которого в два раза выше, чем у другого, оставит углубление в четыре раза глубже, из чего он пришел к выводу, что сила, создаваемая движущимся телом, пропорциональна квадрату его скорости.Тот же принцип применим к кинетической теории газа, где сила молекул, ударяющих по стенкам сосуда, и создает давление газа, пропорциональное квадрату их скорости.
В качестве примера полезно рассмотреть азот, поскольку воздух в основном состоит из азота. Каждая отдельная молекула азота в закрытом контейнере быстро движется по прямой линии, пока не отскочит от другой молекулы азота или от стенки контейнера, по сути, как связка бильярдных шаров.При температуре газа 20 ° C каждая отдельная молекула азота движется со средней скоростью 518 метров в секунду или 1864 км в час. Хотя каждая молекула крошечная, совокупная сила удара, создаваемая всеми молекулами, ударяющими нашу кожу каждую секунду (примерно 3 x 10 27 на квадратный метр), представляет собой давление обычного воздуха на наши тела.
На самом деле молекулы газа в системе движутся с широким диапазоном скоростей, но средняя (средняя) скорость используется для расчета давления и других эффектов.Другими словами, молекулы одного и того же газа демонстрируют распределение скоростей (рис. 4), при этом среднее значение представлено пиком кривой. Одни двигаются быстрее, другие медленнее.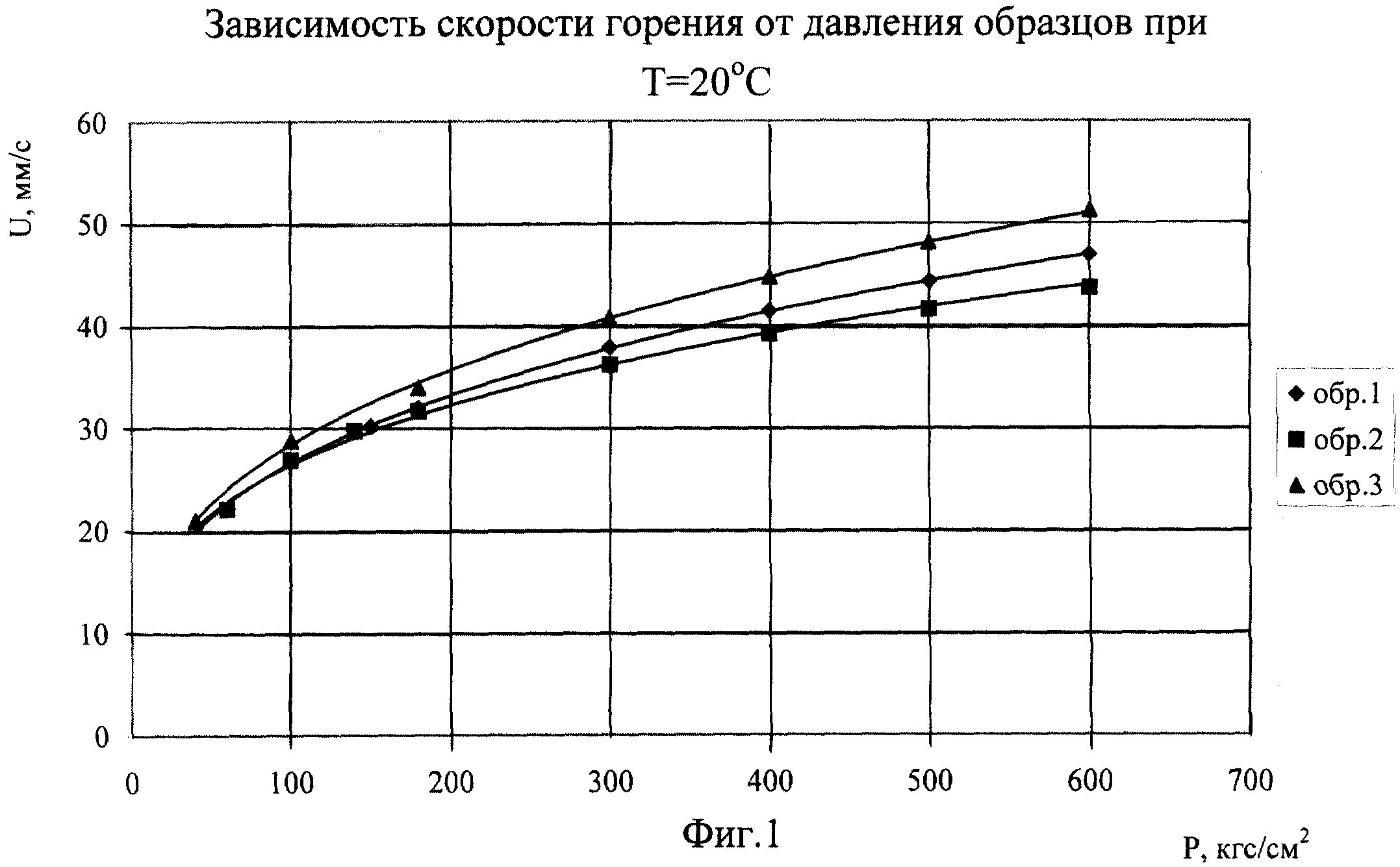
Распределение молекулярных скоростей в газе имеет интересное следствие. Из-за колоколообразной кривой распределения скорости существует значительное количество молекул, скорость которых намного выше (примерно в 6 раз), чем в среднем.Скорость убегания с Земли любого движущегося объекта (включая молекулы газа) составляет 11,2 км в секунду. Самые быстрые молекулы азота будут перемещаться со скоростью 518 × 6 = 3108 метров в секунду. Это намного меньше космической скорости, и поэтому азот не ускользает от земного притяжения.
С другой стороны, молекулы водорода в атмосфере Земли будут двигаться со скоростью 2700 × 6 = 16 200 метров в секунду или 16,2 километра в секунду. Это выше космической скорости Земли. Итак, самые быстрые атомы водорода, находящиеся в хвосте распределения, достаточно энергичны, чтобы преодолеть хватку гравитации.Следовательно, водород улетит в космос, как и гелий. Гравитация Земли удерживает тяжелые газы, но более легкие газы дрейфуют в космос.
В статье выше мы говорили о кинетической теории газов и о том, как ее можно использовать для расчета свойств газа. Мы также рассмотрели взаимосвязь между молекулярной плотностью, длиной свободного пробега, молекулярной скоростью и давлением. Теперь мы обратим наше внимание на обсуждение температуры и кинетической энергии, давления и кинетической энергии, а также типов потока в вакуумных системах.Опять же, мы сосредоточимся на основах, используя фундаментальные сравнения для объяснения концепций, важных для промышленных вакуумных систем.
Значение температуры для кинетической теории газов
Основываясь на атомном понимании мира, в котором мы живем, Кинетическая теория показывает, что свойства газа сильно зависят от скорости их молекул, которая определяет их кинетическую энергию и, следовательно, давление газа. При рассмотрении эффектов кинетической теории также важно понимать влияние температуры.В частности, скорость молекул в газе зависит от его температуры (чем выше температура, тем быстрее движутся молекулы газа).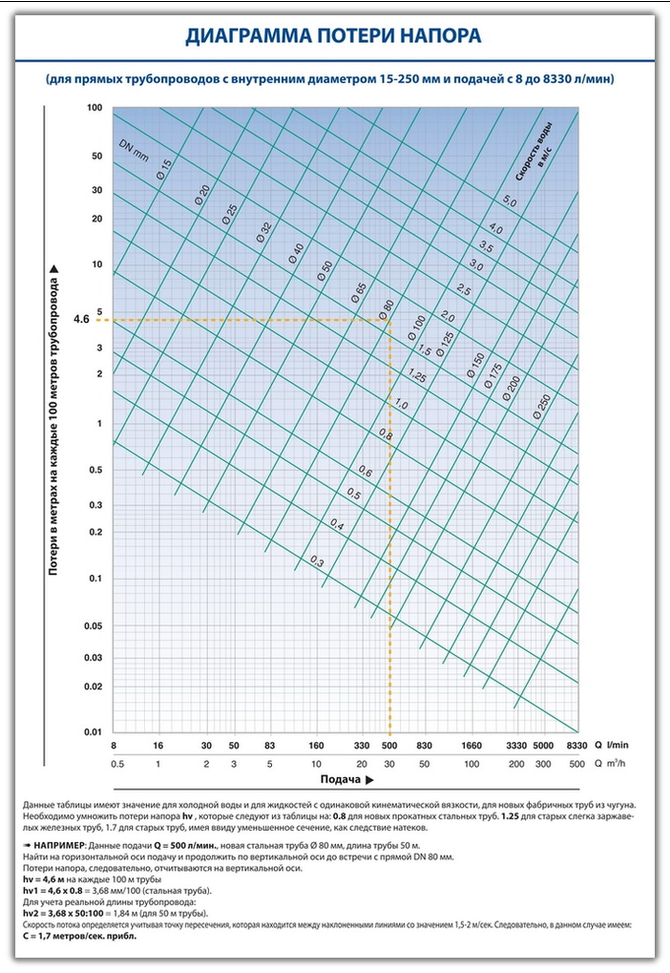 Другой способ думать об этом заключается в том, что температура газа является мерой средней кинетической энергии этого газа.
Другой способ думать об этом заключается в том, что температура газа является мерой средней кинетической энергии этого газа.
Согласно кинетической теории, газ состоит из большого количества крошечных молекул, все в постоянном беспорядочном движении, упруго сталкивающихся друг с другом и с сосудом, в котором они находятся. Давление — это чистый результат силы удара этих столкновений о стенку сосуда.Скорость молекул во время этого движения вовсе не случайна, а следует колоколообразной кривой с предсказуемым распределением около среднего. Молекулярная скорость зависит от веса
молекул и их температуры или собственной тепловой энергии. Таким образом, для данного газа тепловая энергия, содержащаяся в его молекулах, определяет их энергетический уровень и, следовательно, их скорость.
Для того, чтобы полностью оценить влияние температуры на газ, полезно понимать градусы Кельвина (более правильно определяемые просто как Кельвин), которые представляют собой шкалу абсолютной температуры (градусы выше так называемого абсолютного нуля, когда все движение прекращается).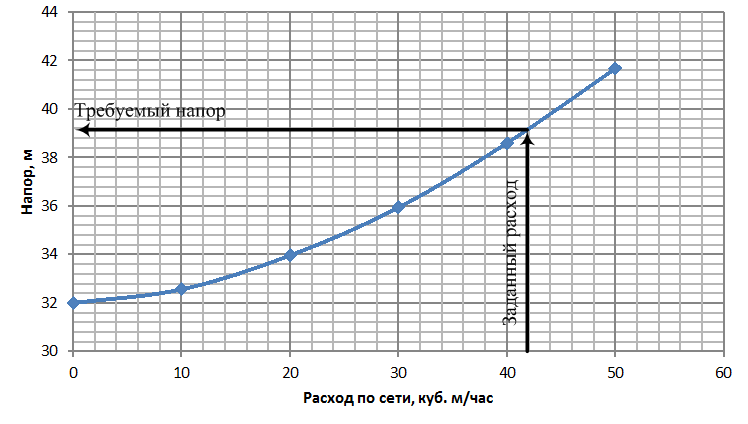 Это истинное измерение кинетической энергии. Поскольку нет температуры меньше нуля и нет объема меньше нуля, абсолютный ноль — это самая низкая возможная температура, при которой все кинетическое движение прекращается, а объем газа уменьшается до нуля.
Это истинное измерение кинетической энергии. Поскольку нет температуры меньше нуля и нет объема меньше нуля, абсолютный ноль — это самая низкая возможная температура, при которой все кинетическое движение прекращается, а объем газа уменьшается до нуля.
Это подтверждается, когда объем газа при нескольких различных температурах измеряется и наносится на график (рис. 1). Когда график затем расширяется до 0 К, объем обращается в ноль. Имейте в виду, что молекулы газа по отдельности не имеют нулевого объема, но пространство между молекулами приближается к нулю.Хотя абсолютный ноль никогда не был достигнут, на небольших образцах были достигнуты температуры до миллиардной кельвина. Для сравнения единиц измерения учитывайте соотношение между K и ° C, при котором абсолютный ноль равен -273,16 ° C (-460,67 ° F). Понимая абсолютную температуру, мы можем обсудить влияние температуры на объем и давление газа.
Рисунок 1 | Объем газа в зависимости от абсолютной температуры 4 Можно видеть, что для данного газа с увеличением его температуры средняя скорость его молекул увеличивается пропорционально квадратному корню из его абсолютной температуры. Возьмем, к примеру, азот (рис. 2). При 300 К (27 ° C или 81 ° F) его молекулы перемещаются в среднем со скоростью 400 метров в секунду (1312 футов в секунду или 894 миль в час). Когда абсолютная температура увеличивается в 4 раза, до 1200 K (927 ° C или 1700 ° F), его средняя молекулярная скорость увеличивается в 2 раза (что является квадратным корнем из 4), до 800 метров в секунду. (2624 фута в секунду или 1789 миль в час).
Возьмем, к примеру, азот (рис. 2). При 300 К (27 ° C или 81 ° F) его молекулы перемещаются в среднем со скоростью 400 метров в секунду (1312 футов в секунду или 894 миль в час). Когда абсолютная температура увеличивается в 4 раза, до 1200 K (927 ° C или 1700 ° F), его средняя молекулярная скорость увеличивается в 2 раза (что является квадратным корнем из 4), до 800 метров в секунду. (2624 фута в секунду или 1789 миль в час).
Также обратите внимание на рис. 2, что при более низких температурах кривые становятся более узкими и высокими.При более высоких температурах существует более широкое распределение уровней энергии (и соответствующих молекулярных скоростей) среди популяции молекул. При более низких температурах меньше вариабельность между скоростями различных молекул, и поэтому кривая становится более узкой в основании. Когда (абсолютная) температура газа понимается как мера его кинетической энергии, значение кинетической теории газов в отношении температуры становится ясным. Напомним, что согласно кинетической теории газов давление, оказываемое газом, является суммой сил, оказываемых всеми физическими ударами между молекулами газа и сосудом (или вакуумной камерой, или вакуумным трубопроводом и т. Д.).) содержащий его. Поскольку скорость молекул напрямую связана с температурой (квадратом), давление газа, следовательно, также напрямую связано с температурой, как квадратный корень из его абсолютной температуры.
Напомним, что согласно кинетической теории газов давление, оказываемое газом, является суммой сил, оказываемых всеми физическими ударами между молекулами газа и сосудом (или вакуумной камерой, или вакуумным трубопроводом и т. Д.).) содержащий его. Поскольку скорость молекул напрямую связана с температурой (квадратом), давление газа, следовательно, также напрямую связано с температурой, как квадратный корень из его абсолютной температуры.
Влияние температуры на давление, описанное кинетической теорией, можно проиллюстрировать простым экспериментом с баллоном для вечеринок и жидким азотом (рис. 3). Когда надутый баллон временно погружается в контейнер с жидким азотом, который имеет температуру 77 кельвинов (-196 ° C или -320 ° F), молекулы воздуха внутри него сразу же теряют температуру и теряют кинетическую энергию (т.е.е. их скорость уменьшается). В результате уменьшения скорости молекул происходят две вещи; (а) столкновения между молекулами становятся менее частыми, что позволяет уменьшить пространство между ними, и (б) сила, с которой молекулы сталкиваются со своим контейнером (воздушным шаром), уменьшается, уменьшая давление воздуха, оказываемое на воздушный шар. Это заставляет воздушный шар сжиматься. Уменьшенный объем воздуха пропорционален его абсолютной температуре. Поскольку температура воздуха внутри баллона была снижена с 293 К (20 ° C, комнатная температура) до 77 К, полученный объем составляет 77/293 = 26% от первоначального объема баллона.
Это заставляет воздушный шар сжиматься. Уменьшенный объем воздуха пропорционален его абсолютной температуре. Поскольку температура воздуха внутри баллона была снижена с 293 К (20 ° C, комнатная температура) до 77 К, полученный объем составляет 77/293 = 26% от первоначального объема баллона.
Типы течения в вакуумных системах; Континуум, молекулярный и Кнудсен
Способ, которым газ течет в вакуумной системе, зависит от давления газа. При приблизительном давлении вакуума выше примерно 1 мбар (0,015 фунт / кв. Дюйм) преобладает непрерывный (или вязкий) поток. При таких давлениях молекулы располагаются относительно близко друг к другу, и их столкновения более часты.Следовательно, поток определяется взаимодействием между молекулами. В результате весь объем газа или группу молекул можно заставить двигаться упорядоченным движением, то есть потоком (рис. 4). Это упорядоченное движение накладывается на нормальное случайное движение отдельных молекул или добавляется к нему. Можно представить, что газ при этих давлениях имеет вязкость или липкость, которая позволяет им двигаться упорядоченно из-за внутреннего трения между молекулами. Следовательно, предпочтительная скорость и направление потока молекул будут такими же, как и для макроскопического потока газа.
Можно представить, что газ при этих давлениях имеет вязкость или липкость, которая позволяет им двигаться упорядоченно из-за внутреннего трения между молекулами. Следовательно, предпочтительная скорость и направление потока молекул будут такими же, как и для макроскопического потока газа.
Молекулярный поток, с другой стороны, наблюдается при давлениях ниже 0,001 мбар (0,000015 фунт / кв. Дюйм), что находится в диапазоне высокого и сверхвысокого вакуума. При таких давлениях межмолекулярные столкновения происходят гораздо реже из-за того, что между молекулами газа очень много места (рис. 5). Молекулы движутся свободно без взаимного вмешательства, поэтому упорядоченный групповой поток невозможен.Молекулы по отдельности движутся по прямой линии, не сталкиваясь, пока не ударяются о стенку сосуда или трубы, содержащей их. Молекулярный поток присутствует там, где длина свободного пробега (среднее расстояние, которое должна пройти молекула до столкновения с другой молекулой) намного больше диаметра трубы, через которую проходит газ, и поэтому молекулы могут свободно перемещаться, пока не столкнутся с стенки трубы. Как следствие, частица газа может двигаться в любом произвольном направлении в высоком вакууме, и макроскопический сплошной поток больше невозможен.
Как следствие, частица газа может двигаться в любом произвольном направлении в высоком вакууме, и макроскопический сплошной поток больше невозможен.
В переходной области между непрерывным потоком и молекулярным потоком преобладает поток Кнудсена. В этом диапазоне как столкновения стенок, так и межмолекулярные столкновения влияют на определение характеристик потока.
Насосная техника в диапазоне сплошных и молекулярных потоков
Вакуумные насосы, которые работают в диапазоне непрерывного (вязкого) потока, такие как нагнетатели Рутса, винтовые насосы, кулачковые насосы и пластинчато-роторные насосы, работают, перемещая молекулы как группу.Их преимущество заключается в использовании взаимодействия между молекулами (вязкости газа) в своих интересах. Они создают всасывание, чтобы втягивать объем газа ко входу насоса, затем проталкивают его через механизм насоса и вытесняют его при атмосферном давлении. В результате они могут обеспечить высокую производительность и быструю откачку на этапах черновой обработки и низкого вакуума.
В результате они могут обеспечить высокую производительность и быструю откачку на этапах черновой обработки и низкого вакуума.
Насосы, используемые для создания высокого и сверхвысокого вакуума, включают диффузионные насосы, криогенные насосы и ионные насосы, и должны работать в диапазоне молекулярных потоков.Поэтому в них используется другая технология, чем в черновых и низковакуумных насосах. Поскольку настоящего макроскопического потока в молекулярном диапазоне нет, насосы, используемые при высоком и сверхвысоком вакууме, не могут «вытягивать» газ из вакуумной камеры. Скорее их режим работы заключается в простом улавливании молекул, которые случайным образом попадают во впускное отверстие насоса. В результате, когда давление в камере достигает диапазонов высокого и сверхвысокого вакуума, снижение давления становится намного медленнее, и работа насоса становится более сложной.
Чтобы понять работу насоса в диапазоне молекулярных потоков, полезно представить молекулы в вакуумной камере в виде бильярдных шаров на бильярдном столе (рис. 6), имеющий только один открытый карман, имитирующий вход насоса. Если все шары приводятся в движение в случайных направлениях, например, после разрыва, но могут продолжать отскакивать от бамперов без замедления (как это делают молекулы газа после столкновения со стенками камеры), некоторые из них начнут падать. в карман. Так как луза не имеет возможности «притягивать» шары к себе, она полагается на вероятность того, что шарик упадет в нее. Вначале, пока есть больше шаров, высока вероятность того, что шар упадет в лузу, и шары удаляются довольно быстро.Чем больше шаров попадает в лузу, тем меньше их остается, что снижает вероятность попадания шара в лузу. В конце концов, остается всего несколько шаров, и вероятность попадания шара в лузу становится очень низкой. На этом этапе дальнейшее удаление мяча очень маловероятно, и с практической точки зрения шары не будут удалены в разумный промежуток времени. Достигнут эквивалент сверхвысокого вакуума.
6), имеющий только один открытый карман, имитирующий вход насоса. Если все шары приводятся в движение в случайных направлениях, например, после разрыва, но могут продолжать отскакивать от бамперов без замедления (как это делают молекулы газа после столкновения со стенками камеры), некоторые из них начнут падать. в карман. Так как луза не имеет возможности «притягивать» шары к себе, она полагается на вероятность того, что шарик упадет в нее. Вначале, пока есть больше шаров, высока вероятность того, что шар упадет в лузу, и шары удаляются довольно быстро.Чем больше шаров попадает в лузу, тем меньше их остается, что снижает вероятность попадания шара в лузу. В конце концов, остается всего несколько шаров, и вероятность попадания шара в лузу становится очень низкой. На этом этапе дальнейшее удаление мяча очень маловероятно, и с практической точки зрения шары не будут удалены в разумный промежуток времени. Достигнут эквивалент сверхвысокого вакуума.
Ранее в этой статье мы говорили о кинетической теории газов и, в частности, мы показали, как движение атомов влияет на такие принципы, как молекулярная плотность, среднее свободный пробег и молекулярная скорость, и как они используются для анализа макроскопических свойств газов, таких как давление, температура и поток в вакуумной среде. Ниже мы обсудим связанные темы потока газа, скорости газа, проводимости, диффузии и эффузии, снова сосредоточившись на фундаментальных концепциях.
Ниже мы обсудим связанные темы потока газа, скорости газа, проводимости, диффузии и эффузии, снова сосредоточившись на фундаментальных концепциях.
Скорость потока газа
При разработке и использовании вакуумных систем очень важно уметь предсказать время, необходимое для снижения давления до желаемого уровня. Поскольку это время напрямую связано со скоростью потока газа в системе, важно понимать, что влияет на скорость потока газа.Практическое значение имеет влияние диаметра труб, изгибов труб и таких устройств, как фильтры и конденсаторы. Явления потока не так легко понять, если не принять во внимание различные свойства газа в так называемом континуальном и молекулярном диапазонах потоков.
Заблокирован (заблокирован) поток
При низких скоростях потока в сплошной среде или в вязком диапазоне газовых потоков (возникающих при давлениях выше примерно 1 мбар) скорость потока через трубу или отверстие прямо пропорциональна перепаду давления в трубе или отверстии. Это изменяется, когда скорость потока газа достигает скорости звука, называемой скоростью звука (приблизительно 1223 км / ч или 760 миль в час), которая является скоростью звука в этом газе.
Это изменяется, когда скорость потока газа достигает скорости звука, называемой скоростью звука (приблизительно 1223 км / ч или 760 миль в час), которая является скоростью звука в этом газе.
Дальнейшее увеличение давления не приведет к увеличению расхода (рис. 7). Это состояние называется закупоркой потока. Дросселирование потока возникает, когда перепад давления на отверстии или в трубе таков, что давление на соотношении между стороной высокого давления и стороной низкого давления отверстия достигает определенного значения, специфичного для этого газа.Для воздуха это значение составляет 52,8% (P IN / P OUT = 0,528).
Это очень важно при удалении воздуха из вакуумной камеры. Когда вентиляционное отверстие открыто, воздух при атмосферном давлении втекает в камеру со скоростью, не превышающей скорость звука, независимо от того, насколько низкое давление внутри камеры. По мере того, как вентиляция продолжается и камера заполняется газом, давление внутри камеры повышается, пока не достигнет P ATM x 0,528, или 528 мбар (7,76 фунт / кв. Дюйм). После того, как степень давления поднимается выше этой точки, скорость потока становится пропорциональной разнице давлений в вентиляционном отверстии.Вывод заключается в следующем: поскольку скорость газового потока не может быть увеличена выше скорости звука, единственный способ увеличить скорость вентиляции камеры — это использовать более крупный вентиль.
Дюйм). После того, как степень давления поднимается выше этой точки, скорость потока становится пропорциональной разнице давлений в вентиляционном отверстии.Вывод заключается в следующем: поскольку скорость газового потока не может быть увеличена выше скорости звука, единственный способ увеличить скорость вентиляции камеры — это использовать более крупный вентиль.
Электропроводность
Электропроводность — это характеристика вакуумного компонента или трубопровода, который «проводит» газ через систему. По аналогии с электрическими системами, где проводимость провода позволяет течь электронам через цепь, вызванную электрическим потенциалом, проводимость в вакуумной системе разрешает поток молекул газа через вакуумную систему, вызванный перепадом давления, создаваемым насосом.При выборе вакуумного насоса и других компонентов необходимо тщательно учитывать электропроводность, чтобы предотвратить снижение скорости откачки и увеличение времени простоя. Производительность насоса должна быть увеличена с учетом сопротивления или обратной проводимости.
Производительность насоса должна быть увеличена с учетом сопротивления или обратной проводимости.
Проводимость выражается в единицах объемного расхода, деленного на падение давления, выраженного в литрах в секунду или кубических футах в минуту. Проводимость между двумя точками определяется как расход газа, протекающего через устройство, деленный на результирующее падение давления.
Электропроводность наибольшая в области вязкого потока (Cv), наименьшая в области молекулярного потока (Cm) и промежуточная в области переходного потока (Ct). Другими словами, Cm
При более высоком давлении, при котором возникает вязкое течение, молекулы газа располагаются относительно близко друг к другу и движутся вместе как группа. Обратите внимание, что на Рисунке 8 давление в камере больше, чем давление на входе вакуумного насоса. В диапазоне вязких потоков столкновения между молекулами часты, так как они расположены относительно близко друг к другу, и когда возникает перепад давления, молекулы движутся как группа. С другой стороны, в молекулярном диапазоне (рис. 9) молекулы так разбросаны, что столкновения бывают очень редко.Следовательно, когда на конец камеры трубы оказывается давление, молекулы не могут «проталкивать» друг друга через трубу, потому что они почти никогда не сталкиваются, а скорее перемещаются независимо. Насос должен полагаться на беспорядочное движение молекул, чтобы попасть во впускное отверстие насоса, и в это время они просто захватываются. Насос не может притягивать к себе молекулы.
Рисунок 8 | Поток через трубу в непрерывном диапазоне Рис. 9 | Поток через трубу в молекулярном диапазоне.
9 | Поток через трубу в молекулярном диапазоне.Несколько важных фактов о проводимости, заслуживающих внимания:
1. Проводимость системы можно рассчитать. Электропроводность трубы обычно берется из значений на диаграммах и зависит от диаметра трубы, длины трубы, расхода и давления. Значения проводимости для таких компонентов, как клапаны, фильтры и ловушки, публикуются их производителями и основаны на эмпирических значениях.
2. Электропроводность изменяется во время трех режимов потока через систему: непрерывного потока, молекулярного потока и потока Кнудсена (переход между ними).Напомним, что непрерывный поток происходит при более высоком давлении (низкий вакуум), а молекулярный — при более низком давлении (высокий вакуум). Следовательно, проводимость данного вакуумного компонента не является постоянной величиной, а зависит от давления в системе. Поэтому при вычислении проводимости необходимо понимать, что в этом диапазоне могут применяться только значения проводимости, применимые к определенному диапазону давлений.
3. Для выбора вакуумного насоса необходимо рассчитать общую проводимость проектируемой системы.Обычно это делается приблизительно с добавлением запаса прочности. Затем можно выбрать насос для обеспечения желаемой скорости потока в каждом диапазоне давления и совокупного потока, определяемого с течением времени.
4. В области молекулярного потока значение проводимости не зависит от давления (рис. 10). Кривые сглаживаются в нижнем диапазоне давления. Другими словами, при высоком и сверхвысоком вакууме проводимость остается постоянной при разных давлениях. Это не так в диапазонах континуума и Кнудсена, где проводимость сильно зависит от давления.
5. Геометрия системы:
a. Лучше всего подходят трубы меньшей длины и большего диаметра
b. Диаметр коллектора и трубопровода должен быть таким же или больше, чем входное отверстие вакуумного насоса
c. Система откачки должна быть физически расположена как можно ближе к камере
d. Количество изгибов, изгибов и поворотов должно быть не менее
Effusion
Эффузия описывает способ, которым газы проходят через небольшое отверстие из области с более высоким давлением в область с более низким давлением (рис.11). Это относится к вакуумным системам, поскольку объясняет действие утечек вакуума в условиях высокого вакуума, когда преобладает молекулярный поток.
Чтобы понять излияние, рассмотрим барьер между областями низкого давления (высокого вакуума) и высокого давления (рис. 11). Если в барьере создается очень маленькое (диаметр меньше среднего пути) точечное отверстие, кинетическое движение молекул газа диктует, что молекулы пройдут через отверстие, когда их путь случайным образом направляет их через него.Напомним, что средний путь (таблица 1) — это расстояние, которое проходит молекула газа до столкновения с другой молекулой. Корневой средний путь сильно варьируется в диапазоне давлений, в котором работают вакуумные системы. Поскольку в высоком вакууме любое отверстие или утечка в вакуумной системе меньше этого расстояния, газ не будет течь через отверстие в упорядоченном групповом движении. Скорее, со временем это случайное движение заставляет некоторые частицы в конечном итоге проходить через отверстие.
Рисунок 11 — Газ проходит через отверстие за счет истечения (любезно предоставлено компанией Prenhall.com)Законы Грэма гласят, что скорость истечения газа больше для более легких газов, чем для более тяжелых. Это связано с тем, что более легкие молекулы движутся быстрее. Поскольку для молекулы единственный способ вырваться из своего сосуда — это «ударить» в дыру, чем быстрее движутся молекулы, тем больше вероятность того, что молекула ударится в дыру и истечет. Поэтому водород и гелий, которые имеют низкую молекулярную массу и высокую скорость, будут проходить через утечку намного быстрее, чем воздух.
Таблица 1 | Средний свободный пробег молекулы азота при 0 ° C (адаптировано автором из информации, предоставленной Pfeiffer Vacuum).Эффузия также может использоваться для описания способа, которым молекулы попадают в высоковакуумный насос. Поскольку диаметр вакуумного насоса будет больше, чем длина свободного пробега для давлений ниже примерно 10 -4 мбар, практически все молекулы, которые достигают впускного отверстия, продолжают движение и проходят в насос, поскольку столкновения между молекулами в области впускного отверстия незначительны.Термин «эффузия» также помогает прояснить, каким образом насосы высокого вакуума собирают молекулы, попадающие в насос, а не всасывают молекулы к входному отверстию. Можно сказать, что молекулы истекают через впускное отверстие насоса.
Распространение
Согласно кинетической теории газов, молекулы газа находятся в постоянном беспорядочном состоянии, перемещаясь с разной скоростью и во многих разных направлениях. Из-за своей кинетической энергии при температурах выше абсолютного нуля все частицы претерпевают диффузию или движение из области с высокой концентрацией в область с низкой концентрацией.Скорость этого движения зависит от температуры, вязкости среды и массы молекул. Диффузия вызывает постепенное смешивание разных газов.
Принцип диффузии имеет отношение к области вакуумной техники несколькими способами. Во-первых, диффузия — это средство, с помощью которого молекулы газа проходят через твердый материал, загрязняя вакуумный процесс. Даже если компоненты вакуумной системы могут быть спроектированы без физических утечек, а также клапаны и другие компоненты, которые идеально герметизируют механически, небольшие молекулы, такие как гелий, могут проникать через полимерные уплотнения и даже через металлические стенки вакуумных камер.Для преодоления этого используются различные стратегии, в том числе использование вакуумного насоса для простого удаления вторгающихся молекул и использование материалов с лучшими константами проницаемости.
Другая важная роль диффузии в вакуумных системах связана с диффузионным насосом (рис. 12), который обычно используется для достижения высокого вакуума. Его принцип действия основан на диффузии молекул перекачиваемого газа в перекачиваемую среду, такую как масло или полимер. Как обсуждалось ранее, все насосы высокого вакуума основаны на улавливании молекул газа, а диффузионные насосы способны улавливать молекулы, поддерживая низкую концентрацию молекул газа, диффундирующих в перекачивающую среду.Затем молекулы перекачиваемого газа удаляются из среды посредством конденсации, и эта очищенная среда постоянно повторно вводится, что вызывает дальнейшую диффузию газа, предотвращая насыщение среды газом.
Рисунок 12 | Анатомия диффузионного насоса (любезно предоставлено Edwards Vacuum)Ссылки
- www.grayline.com
- http://web2.uwindsor.ca/courses/physics/high_schools/2005/Brownian_motion/kinetictheory.jpg)
- http: // wps.prenhall.com/wps/media/objects/3311/33/blb1008.html).
- Закон об идеальном газе
- http://2012books.lardbucket.org/books/principles-of-general-chemistry-v1.

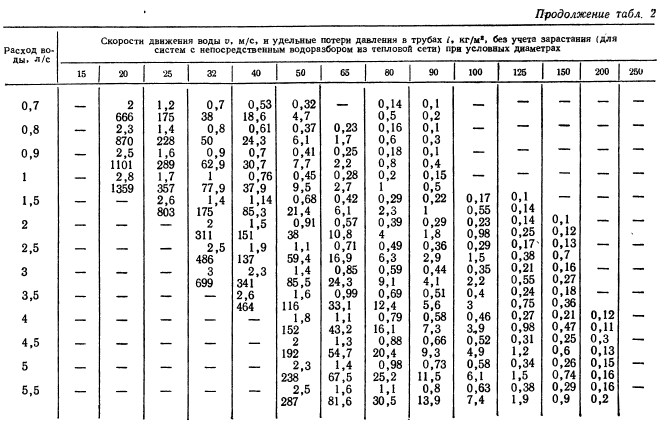

 Типичные значения приведены в таблице 1.{4}} {8 \ eta l} \\ [/ латекс].
Типичные значения приведены в таблице 1.{4}} {8 \ eta l} \\ [/ латекс].